两种GNSS-R镜面反射点搜索算法

刘原华,孙毅,牛新亮

(1.西安邮电大学 通信与信息工程学院,陕西 西安 710121;2.中国空间技术研究院西安分院,陕西 西安710100)

0 引 言

作为一种新型的微波遥感技术、全球卫星导航系统反射(GNSS-R)技术具有丰富的信号源,低成本、低功耗、全天时、全天候等优点,它可以获得各种全球海洋动力学和环境参数如海面高度(SSH),海面风场、海冰和海水盐度. 此外,GNSS-R卫星平台的成本和有效载荷相对较低,结合专用指向天底天线、轨道和星座的参数优化设计,可形成6～8颗卫星星座,完成多项任务,具备优良性能.

在已知接收机坐标情况下,时间延迟和反射信号路径长度的误差主要来自海洋表面的镜面反射点定位误差和大气信号传输误差. 此外,双基雷达系统的输出信噪比与信号传播路径有关,而信号传播路径又与镜面反射点的位置直接相关. 在海面遥感应用中,镜面反射点的精确位置信息也可以用来确定反射信号是来自海面、陆地还是冰面. 镜面反射点作为参考点GNSS-R信号的反射几何及相关参数,其定位误差影响GNSS-R遥感产品的准确性[1].

镜面反射点定位方法可分为物理方法和几何方法. 物理方法以接收信号的处理为基础,几何方法以镜面反射点满足的几何条件为基础进行研究. 现有的镜面反射点搜索方法包括黄金分割法[2]、二分法[3]、Gleason算法[4]、S.C.WU[5]、C.Wagner[6]、椭球面算法[7]、AdaGrad自适应算法[8]等. Gleason算法精度较高,但是迭代次数较多. 黄金分割法迭代较少,算法经典,但仍然存在一定的提升空间. 二分法模型简单,易于计算,不过由于采用的是角度作为迭代依据,因此存在一定的误差. 本文在分析基本几何反射关系的基础上,提出了2种镜面反射点搜索算法,进一步改进镜点搜索的算法.

首先,提出了基于斐波那契法的镜点搜索算法,并和黄金分割法进行比较,从数论的角度证明了其算法的优越性. 另外提出了一种基于求导极值的搜索算法,该方法省去了不断迭代的过程,从而优化了计算. 仿真结果表明,这种算法能够计算出镜点的位置,对镜点的搜索具有一定的意义.

1 GNSS-R基本反射关系

在讨论直射信号与反射信号的关系中,引入了镜面反射点的概念[9],即从反射区域反射的反射信号中路径最短的理论反射点. 其数学表达式为

f=|R-S|+|T-S|=

(1)

式中:R为接收机坐标;T为卫星坐标;S为球面坐标;其大致几何关系如图1所示,图中R为接收机;T为卫星;O为地心;Re为地球半径,在RT线段中一点为P,P所对应的星下点为S,R的星下点为a,T的星下点为b,ar和at分别表示s到R、T之间的仰角.

镜面反射点有以下三个特征:

1)位于椭球面弧段ab上;

2)入射与出射角相等,即ar=at;

3)到R、T点距离和为最短.

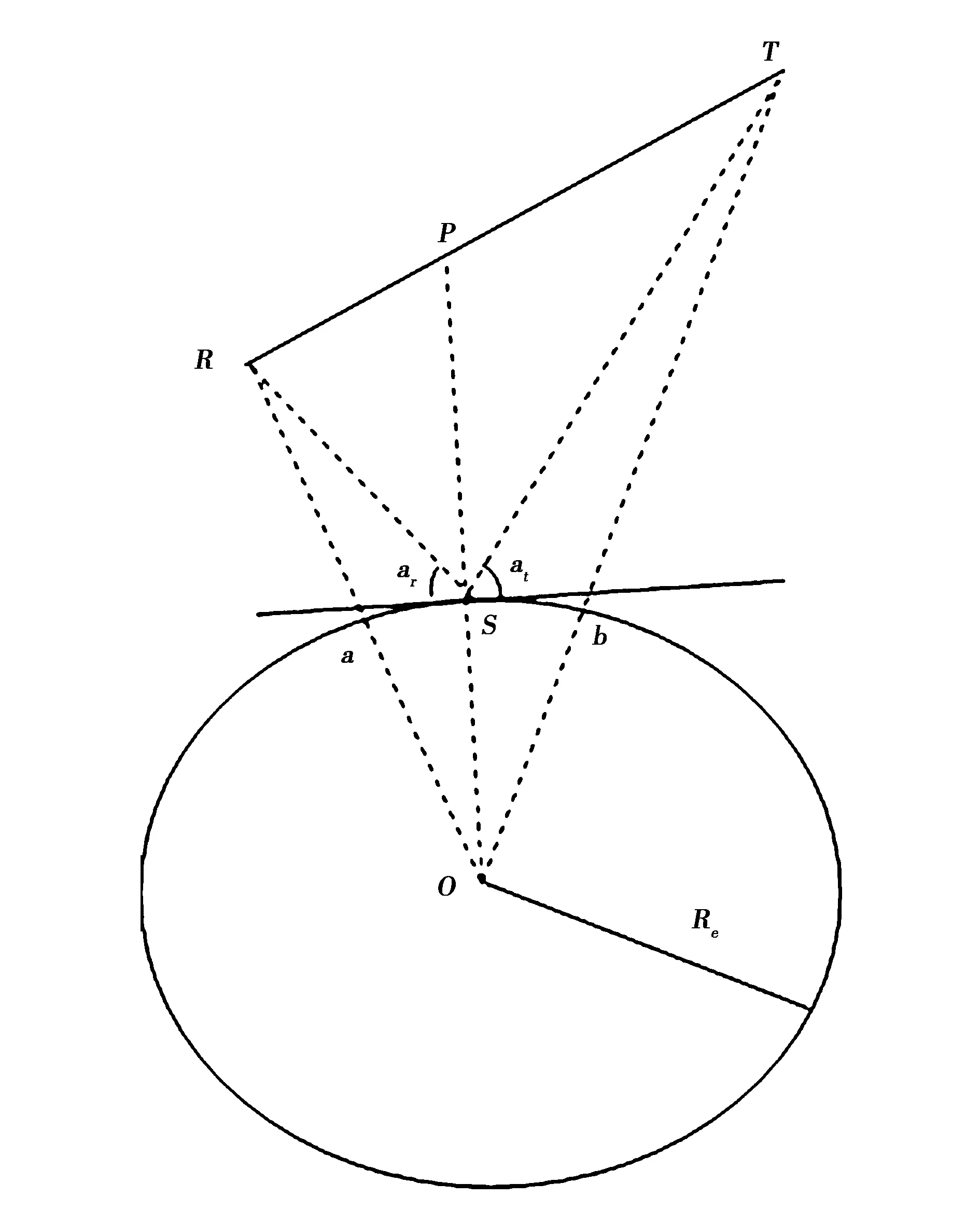
图1 基本几何关系

2 基于斐波那契法的镜点搜索

斐波那契法与黄金分割法类似,也是用于单峰函数. 在计算过程中,也是第一次迭代需要2个试探点,与黄金分割法的主要区别在于区间长度缩短比例不是常数,而是斐波那契数[10]. 由于斐波那契数列自身规律,迭代时相较黄金分割法有一定提升,因此带来了计算次数的减少.

设有数列{Fk},满足条件:

(2)

可将斐波那契数列列表如表1所示.

表1 斐波那契数列

k0123456…Fk11235813…

其通项:

(3)

斐波那契在迭代中计算试探点的公式:

(4)

其具体计算步骤如下:

1)给定初始区间[R,T]和最终区间长度L=1 m,求计算函数值的次数n. 使

Fn≥|R-T|/L.

(5)

置k=1,计算试探点λ1和μ1:

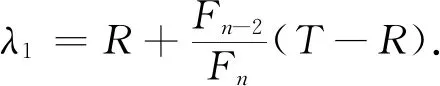
(6)

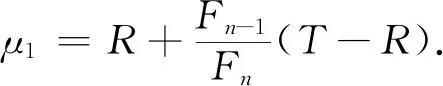
(7)

计算λ1和μ1所对应的星下点到RT距离和f(λ1)和f(μ1).

2)若f(λ1)>f(uk),则转步骤3);若f(λk)≤f(λk),则转步骤4).

3)令ak+1=λk,bk+1=bk,λk+1=μk

计算试探点μk+1:

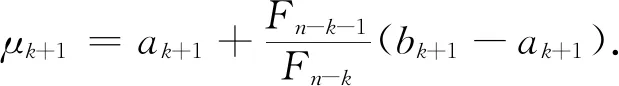
(8)

若k=n-2,则转步骤6);否则,计算函数值f(μk+1),则转步骤5).

4) 令ak+1=ak,bk+1=μk,μk+1=λk,计算试探点λk+1:

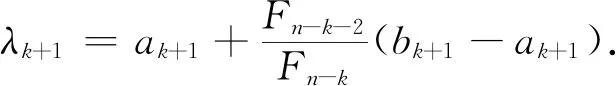
(9)

若k=n-2,则转步骤6);否则,计算f(λk+1),转步骤5).

5)置k=k+1,转步骤2).

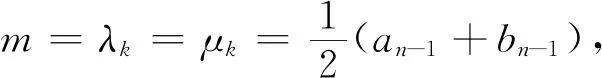
在相同n次迭代计算时,用黄金分割法,最终区间长度为

(10)

用斐波那契法,最终区间长度为

(11)

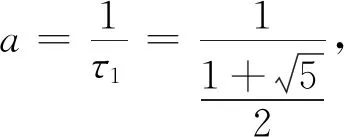
由式(10)～(11)可知:

(12)

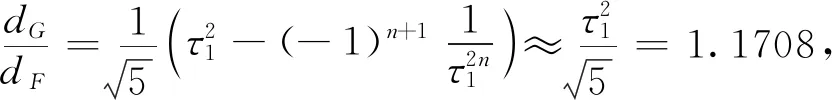
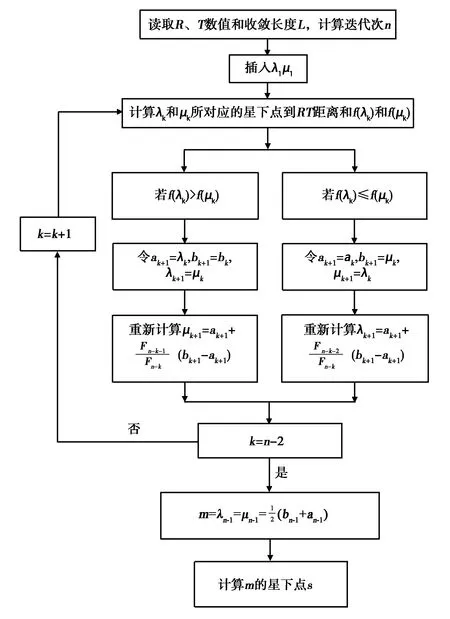
图2 计算流程图

3 基于极值求导的镜点搜索

在WGS84坐标系下,当R(xr,yr,zr)、T(xt,yt,zt)点位置给定之后. 假设变量K∈[0,1],令P=R+k·(T-R)=(xr+k·(xt-xr),yr+k·(yt-yr),zr+k·(zt-zr)),当K从0连续变化到1时,P就取遍了RT线段中的所有点,即RT线段中的点均可用变量K和常数来表示,如图3所示.

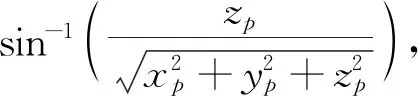
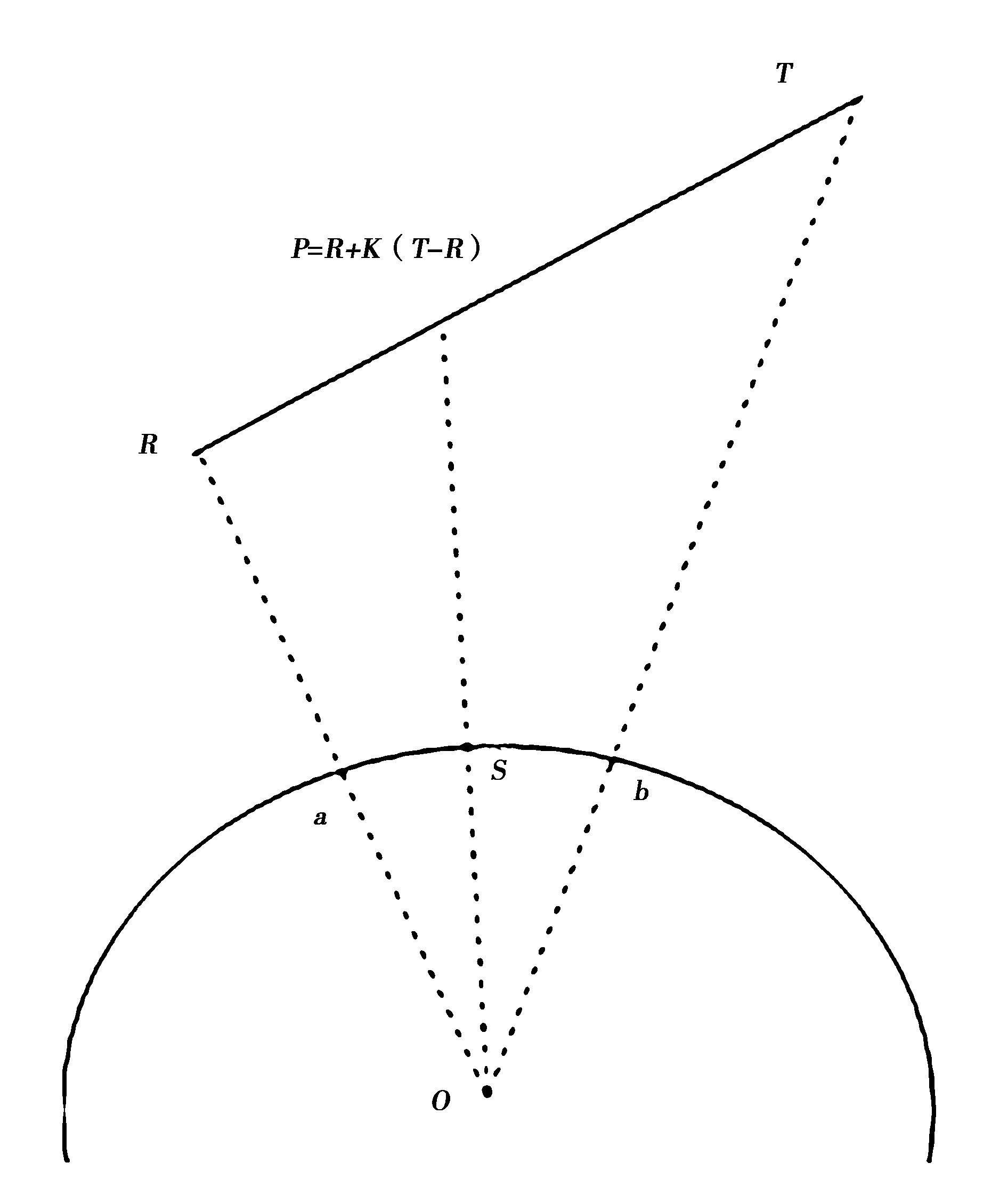
图3 变量K表示RT线段

2)由映射算法知此纬度所对应的球径ρ

凳子上摆了本书。书打开，封皮朝上，我看到了两个字：诗集。我很诧异，柴米河，没几人识字，想不到别呦呦竟爱看书，这一点倒和我一样。我爱看谈狐说鬼的书，诗，几乎不看。

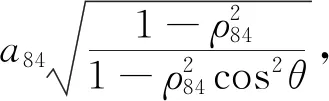
那么P所对应的星下点S=p×ρ=

3)R、T为已知数,即可建立星下点S到R、T的距离和函数:

f(k)=

其图像如图4所示.

图4 函数大致图像

4)此时,镜面反射点的搜索问题,也就转化函数f(k)的极值问题. 利用MATLAB求导函数对函数f(k)进行一阶求导,得到f′(k). 再利用solve解方程函数求解方程.

f′(k)=0.

求解出K值之后,回代入P的坐标,即可求得所对应的星下点S,此点即为镜面反射点.

传统做法大部分基于尝试法,在RT区间内不断进行迭代,根据距离最小或者角度相等的原则,不断缩小搜索区间,最终区间小于一定长度即可得到目标点. 而这样的做法在函数形式已知的情况下较为冗余,增加了算法编程的复杂度.

本文做法基于距离和函数的极值进行求导,相较二分法等基于角度进行不断迭代的做法,避免了由于径向和法向不统一而带来的问题. 同时,本文算法只需要一步求导、一步解方程,相较黄金分割法,又省去了不断迭代的步骤,因此优化了计算. 对镜点的搜索具有一定参考意义.

4 仿真分析

本文采取导航模拟器生成全球卫星导航系统(GNSS)接收机和卫星在WGS84坐标系下的位置信息,接收机R的坐标为[-1747836.86, 4316984.79,-5091148.03],卫星T的坐标为[18524153.94,1465929.77,-19218107.19]. 镜面反射点的参考坐标为[-648295.67,3698445.399,-5138472]. 基于MATLAB对本文所提出的方法进行四次仿真,阈值选取1 m. 通过分析四种方法的计算结果、迭代次数、计算时间,比较说明本文提出的两种方法的正确性,优越性. 由于篇幅原因,在此仅列出一次仿真的结果，如表2所示.剩余仿真结果以柱状图的形式展示如图5和图6所示.

表2 镜面反射点位置估计仿真

图5 和参考点之间的距离

图6 四次仿真的计算时间

如表2所示,极值求导做法距离参考点的距离是最短的,而黄金分割法和斐波那契法则次之,二分法的距离最远.

进行多次仿真后,图5显示前三种方法的结果基本都在10 m以内,极值求导的距离是最小的,二分法则偏离参考点50 m左右. 斐波那契法偏离的距离要小于黄金分割法但是多于极值求导. 其主要原因在于二分法收敛原则与其他方法不同.

从四次计算的时间结果来看,极值求导的时间少于黄金分割法,几近于斐波那契.而二分法的计算时间是最少的,其根本原因在于二分法模型简单,每一次计算只需要求解其中间的一个点的RT距离和,而黄金分割法和斐波那契法相对复杂一些. 同时,极值求导的时间略微少于黄金分割法,近似等于斐波那契法. 综上分析,斐波那契法在偏移距离和计算时间上对传统做法略有提升. 而极值求导在偏移距离上有一定幅度的提升,在计算时间上和传统做法相近.

5 结束语

随着GNSS的迅速发展,针对镜点搜索的需要,本文提出2种镜面反射点搜索算法. 首先提出了斐波那契算法,从数论角度证明了该方法相较黄金分割法有一定提升,进一步减少了迭代次数. 另外,本文提出了基于极值求导的搜索方法,相较传统做法,它省去了不断迭代的过程,采用极值求导的思想计算出镜点,具有一定的优越性. 最后采用导航模拟器生成的数据进行仿真,结果表明,两种方法均可以有效计算出镜面反射点的位置,具有一定的借鉴意义.