一种用于BDS-3接收机的分段Hermite插值方法
2020-09-18安云飞
安云飞
(1. 中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2. 卫星导航系统与装备技术国家重点实验室,河北 石家庄 050081)
0 引 言
随着北斗三号卫星导航系统(BDS-3)的建设,对接收机技术提出了更高的要求,包括跟踪卫星数、定位频度、定位精度和测速精度等. 尽管处理器技术也在同步发展,但是在多系统多频点同时定位或者定位频度10 Hz及以上情况下,仍有必要在保证精度的情况下降低定位解算的运算复杂度. 每次定位解算均需获取每颗卫星的位置、速度信息,常规方法采用广播星历直接计算,涉及众多的复杂运算,耗时巨大. 国内外常采用多项式插值的方法降低卫星位置、速度运算时间,包括拉格朗日插值、牛顿插值、样条插值和Hermite插值等.
文献[1]最早比较了不同阶数的分段Hermite插值与三次样条插值在不同结点间距情况下,对卫星位置和速度插值精度与效率的影响. 文献[2]提出了一种加“窗”的牛顿插值多项式,与三阶Hermite插值相比提高了插值精度与结点间距,代价是多项式的阶数和运算复杂度均有增加. 文献[3]比较了几种常见插值算法的特性,并指出拉格朗日插值运算量大,增减节点时基函数需要重新计算,而且高阶时容易产生龙格现象;牛顿插值在增加结点时,只需计算一次更高阶的差商,但其精度不高.
以上研究均是基于全球定位系统(GPS)或者北斗二号卫星导航系统(BDS-2),而BDS-3在卫星星历参数、卫星轨道精度、定位精度方面均有改进,卫星位置、速度和加速度计算公式也有改变. 因此,研究多项式插值在BDS-3卫星轨道中的计算精度和效率是必要的.
本文推导了BDS-3卫星速度、加速度解算公式,同时提出一种分段Hermite插值方法. 该方法分别构造位置、速度的三次Hermite插值多项式,在运算复杂度不增加的情况下,提升了卫星速度插值精度. 所提方法公式简单、便于编程,并采用作者单位自研接收机对所提方法插值精度、效率进行了验证,同时对比了Hermite插值、分段三次Hermite插值和分段五次Hermite插值.
1 BDS-3卫星速度和加速度
文献[1]给出了GPS NAV电文的卫星位置、速度和加速度计算公式;文献[4]给出了GPS NAV电文的卫星速度公式推导过程;文献[5]给出了GPS NAV电文和CNAV/CANV-2电文在计算卫星位置时的差别;文献[6]给出了BDS-3 CNAV1电文的编排格式和卫星位置计算公式. 本文直接给出基于BDS-3的卫星速度和加速度计算公式,其推导过程暂不赘述.
1.1 CNAV1导航电文卫星速度计算
下面给出BDS-3 CNAV1电文中卫星速度的计算公式:
(1)

(2)
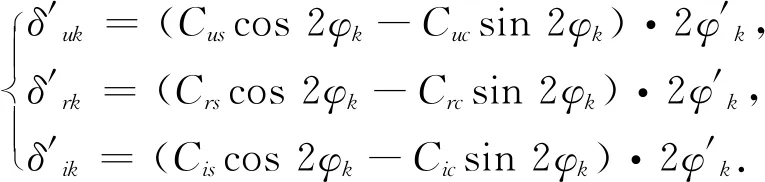
(3)
(4)
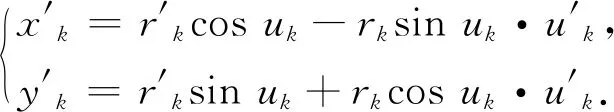
(5)
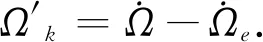
(6)
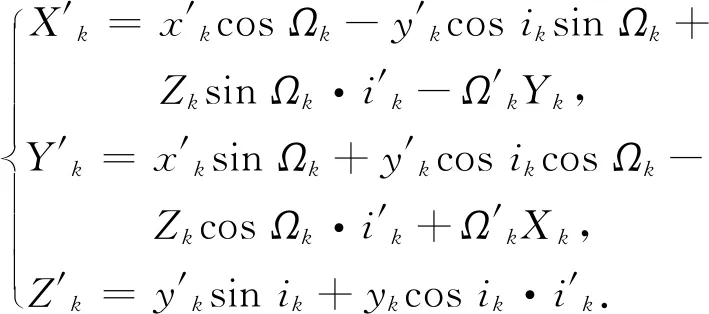
(7)
式中:角标′表示一阶导数;式(1)~(7)中出现的电文播发参数含义如表1所示.

表1 电文播发参数含义表
式(1)~(7)中出现的非播发参数如表2所示.

表2 电文播发参数含义表
1.2 CNAV1导航电文卫星加速度计算
下面给出BDS-3 CNAV1电文中卫星加速度的计算公式:

(8)
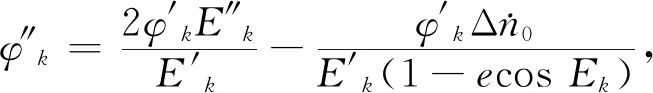
(9)
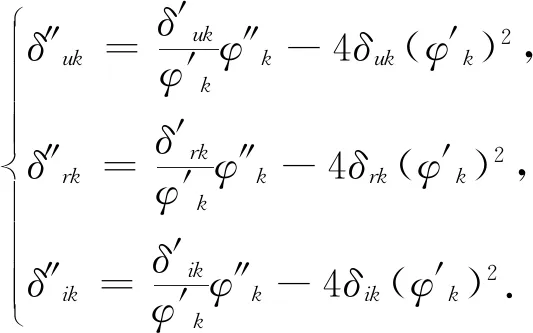
(10)
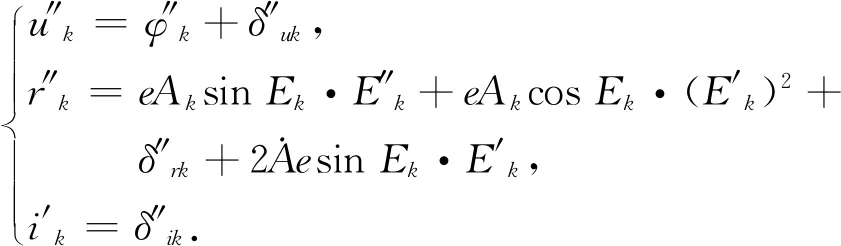
(11)

(12)
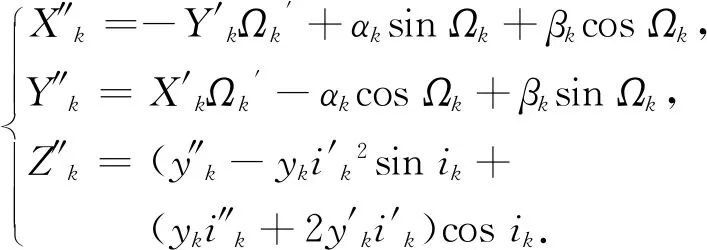
(13)
式(13)中αk和βk分别表示为:
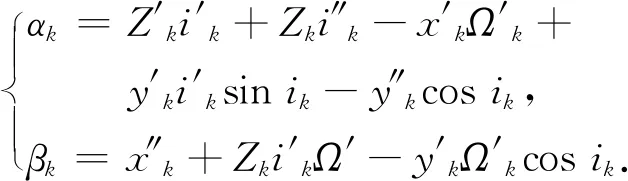
(14)
式中,角标′和″分别表示一阶导数和二阶导数.
2 Hermite插值多项式
Hermite插值不但要求在结点上的函数值相等,还要求对应的导数值也相等,它是一种光滑的插值方法.
下面构造Hermite插值多项式. 设已知节点a≤x0≤x1≤x2…≤xn≤b上,yj=f(xj),mj=f'(xj),(j=0,1,…,n),这里给出了2n+2个条件,可以唯一确定一个次数不超过2n+1的多项式:
H2n+1(x)=a0+a1x+…+a2n+1x2n+1.
(15)
写成用插值基函数表示的形式
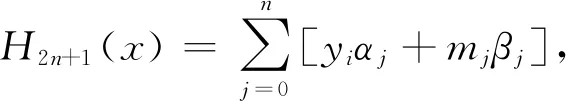
(16)
式中:
(17)
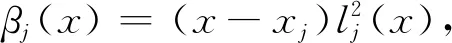
(18)

(19)
Hermite插值和拉格朗日插值有类似的局限性,在增减结点时基函数需要重新计算,高阶情况下容易出现龙格现象. 分段Hermite插值多项式可以比较好地解决此问题.
3 分段Hermite插值多项式
3.1 分段三次Hermite插值多项式
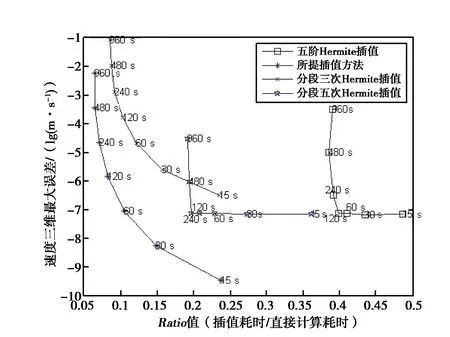
人们常采用分段插值来克服龙格现象.下面介绍分段三次Hermite插值多项式. 设已知节点a=x0 1)In(x)∈C1[a,b]; 3) 在每个小区间[xk,xk+1](k=0,1,2,…,n-1). 是三次多项式. 则称In(x)为分段三次Hermite插值函数. 若用插值基函数表示,则在整个区间[a,b]上,In(x)的表示式为 (20) 插值基函数αi(x)和βi(x)的形式分别为 αi(x)= (21) βi(x)= (22) 分段五次Hermite插值相比分段三次Hermite插值具有更高的精度. 参考文献[7]给出分段5次Hermite插值多项式公式. 设已知节点a=x0 1)φ(x)∈C1[a,b]; 2)φ(xj)=yj,φ′(xj)=mj,φ″(xj)=nj,j=0,1,2,…,n; 3)在每个小区间[xk,xk+1][k=0,1,2,…,n-1].均为次数≤5的代数多项式,则称φ(x)为分段五次Hermite插值函数. 若用插值基函数表示,则在整个区间[a,b]上,φ(x)的表示式为 (23) 为了公式表示方便,新增如下表达式: (24) hi=xi-xi-1. (25) 用l表示li(x),则插值基函数αi(x)、βi(x)和γi(x)的形式分别为 (26) βi(x)= (27) γi(x)= (28) 以上章节给出了BDS-3 CNAV1导航电文卫星速度和加速度的计算公式,并介绍了Hermite插值、分段三次Hermite插值和分段五次Hermite插值. 这几种插值方案均可用于卫星位置、速度的计算. 通常我们将卫星位置信息构造为多项式表达,然后对多项式进行微分可以得到卫星速度的计算公式. Hermite插值的公式计算和导数计算比较复杂,增减节点需要重新计算基函数,高阶情况容易产生龙格现象;分段三次Hermite插值在文献[1]中被认为是最具性价比的方案,在结点间距100~200 s时,位置精度可以达到10 cm,速度精度可以达到1 mm/s;分段五次Hermite插值在保证精度的情况下插值间距可以达到20 min,但是运算量相对有显著提升. 本文提出一种位置和速度分别进行分段三次Hermite插值的方案,可以免去多项式求导数的计算过程,而且位置多项式与速度多项式的基函数可以复用. 由于本方案利用了卫星加速度信息,插值得到的卫星速度精度比分段三次Hermite插值采用位置多项式函数微分得到的速度精度高. 下面给出本方案的具体计算过程. 参考式(20),卫星位置和卫星速度的X、Y、Z方向可以表示为如下多项式: (29) (30) (31) (32) (33) (34) 评价卫星轨道插值方法优劣主要依据插值结点间距、插值计算精度和插值方法运算效率. 插值算法的目的就是保证卫星位置和速度计算精度的前提下,尽量减小运算的耗时. 插值结点间距越大可以减少直接用星历计算卫星位置、速度或者加速度的频度,但是更大的结点间距需要更高次数的插值多项式才可以保证其精度. 下面用试验数据对比分析本文所提插值方法与其他几种插值方法. 用采集回放仪器对天采集B1C频点信号,然后用作者单位自研接收机接收采集回放仪播放的B1C频点CNAV1广播星历,在接收机内部分别应用几种插值方法计算卫星位置和速度,并统计其精度和耗时情况. 应用接收机可以真实反映插值方法性能. 计算卫星位置的星历取自UTC时间2020年5月9日06∶00-07∶00的CNAV1电文广播星历,结点起始位置为星历参考时间,结点间距分别取15 s、30 s、60 s、120 s、240 s、480 s和960 s,定位频度按照1 Hz计算,卫星位置插值误差效果如图1所示. 由图1所示,横轴表示插值运算耗时(包括结点采用直接运算的时间和中间插值点采用多项式运算的时间)与直接采用广播星历计算耗时的比值,纵轴表示在插值点内卫星位置插值结果与直接计算结果的三维最大差值. 图中分别画出了五阶Hermite插值、分段三次Hermite插值、分段五次Hermite插值以及本文所提方法在结点间距分别为15 s、30 s、60 s、120 s、240 s、480 s和960 s时的精度和耗时情况. 其中,分段五次Hermite插值精度最高,本文所提方法与分段三次Hermite插值精度相等,但是耗时略低. 卫星速度插值误差效果如图2所示. 图2 卫星三维速度误差效果图 由图2所示,纵轴表示在插值点内卫星速度插值结果与直接计算结果的三维最大差值. 其中,本文所提方法速度精度和耗时情况均优于分段三次Hermite插值. 本文方法速度精度有所提升是因为引入了卫星加速度信息,虽然在结点处增加了卫星加速度运算,但是省去了多项式微分运算. 由式(16)和式(19)可以看出三阶Hermite插值与分段三次Hermite插值等效,因此本文采用3结点五阶Hermite插值参与比较,由图1和图2可以看出,分段五次Hermite插值在耗时情况和精度方面均优于3结点五阶Hermite插值. Hermite插值无需进行卫星加速度的运算,但是高阶的运算复杂,增减结点基函数需要重新计算;分段五次Hermite插值需要进行卫星加速度计算,更高次数的公式推导将会非常复杂. 本文对Hermite插值在BDS-3中的应用进行了研究,推导了BDS-3卫星速度和加速度计算公式,提出了一种卫星位置、速度分别插值的分段三次Hermite插值方法,并与3点阶Hermite、分段三次Hermite插值和分段五次Hermite插值进行了比较. 试验证明,本文所提方法在卫星速度插值精度方面优于分段三次Hermite插值的多项式微分方法,并且耗时相比有所减少.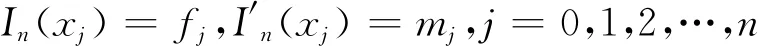
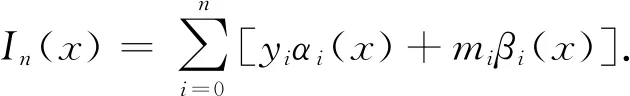
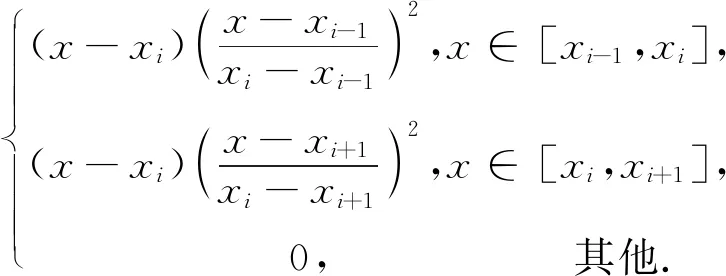
3.2 分段五次Hermite插值多项式
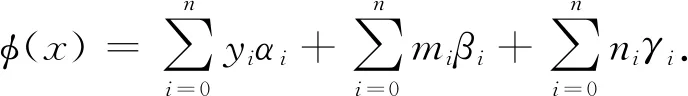
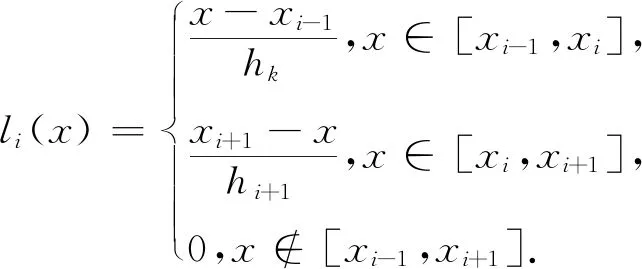
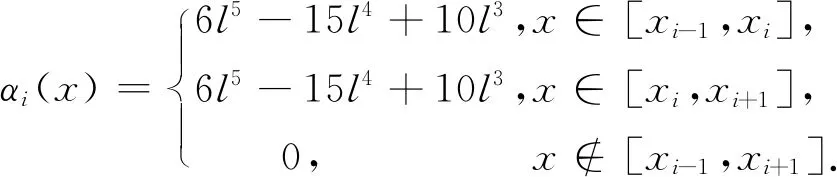
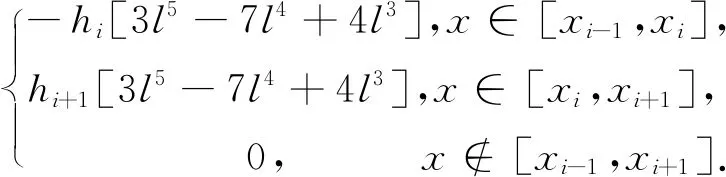
4 Hermite插值分析与优化
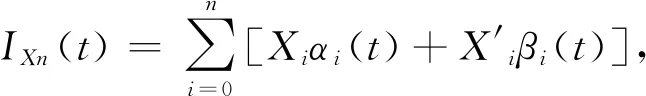
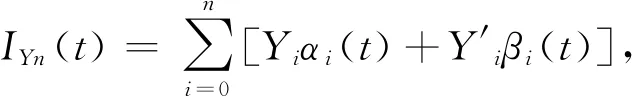
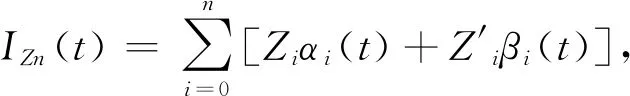
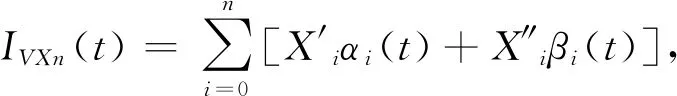
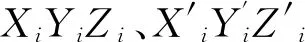
5 实验分析
6 结束语
