北斗GEO卫星精密定轨的最优构型研究与仿真
2020-09-18高杨张强张龙平
高杨,张强,张龙平
(1.北京卫星导航中心,北京 100094;2.国家自然科学基金委员会科学传播与成果转化中心,北京 100085;3.航天宏图信息技术股份有限公司,北京 100195)
0 引 言
北斗卫星导航系统(BDS)是我国自行研制、独立运行的全球卫星导航系统(GNSS),其空间部分采用地球静止轨道(GEO)、倾斜地球同步轨道(IGSO)及中圆地球轨道(MEO)混合星座设计[1-2].2018年12月,完成包括18颗MEO卫星的基本系统建设和1颗GEO卫星发射;2019年12月,又完成了6颗MEO卫星和3颗IGSO卫星发射;2020年3月再发射1颗GEO卫星,即将完成全系统建设[3].目前,北斗三号(BDS-3)GEO卫星除了传统的定位导航授时功能外,还提供星基增强、精密单点定位(PPP)、区域短报文通信等特色服务[4],其精密定轨精度影响服务性能.
随着BDS的应用,世界卫星导航领域已经进入了四大卫星导航系统(BDS、GPS、GLONASS、Galileo)合作的新局面[5].2007年,中国启动了国际GNSS监测评估系统(iGMAS)建设工作[6],目前iGMAS已初具规模,建成并稳定运行的跟踪站有20多个,分别布设在亚太、南极、北极及其他地区;另外有国际IGS的MGEX(IGS Multi-GNSS Experiment network)站和武汉大学的北斗卫星观测实验网[7-8].目前接收BDS信号的全球监测站尽管有百余个,但对GEO卫星精密定轨的分布构型非常不均匀;另外由于GEO卫星具有高轨及静地特性,导致其定轨精度差.国内外学者对导航卫星精密定轨构型进行了大量的分析和实验[9-11],但并未从理论层面推导并给出卫星定轨的最优构型,因此本文根据定位精度因子计算方法,将定轨精度因子参数化,并投影到地面,得到GEO卫星定轨的监测站分布最优构型,并进行了仿真试验,为导航卫星监测站布设提供依据,为顾及地球自转参数、模糊度、电离层延迟、对流层延迟等参数的GNSS精密定轨选站提供参考.
1 卫星定轨的GDOP最优构型构建
1.1 定轨GDOP值推导
目前常用的GNSS定轨方法主要有:动力学定轨、几何法定轨、简化动力学定轨法等.为讨论问题的方便,忽略其他误差及附加参数,在观测历元tk取其距离测量值ρk[12]:
(1)
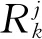
可将观测方程线性化:
Δρk=HkΔX+εk,
(2)
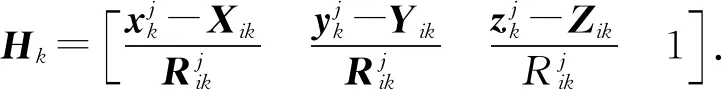
定轨几何精度可定义为
(3)
(4)
式中:σ0为距离测量中误差;tr表示矩阵的迹;q11,q22,q33,q44为权系数阵的主对角线元素;GDOP为精密定轨的构型精度因子[11].
1.2 定轨GDOP值最优解解算
由于定位精度与精度因子的数值大小成反比,因此,定轨中,在定轨算法、测量误差同等的情况下,GDOP值越小,定轨精度越高.
令:
(5)
式中,ei为GEO卫星位置至监测站方向余弦向量,i为测站编号,向量ei满足‖ei‖2=1,为单位方向矢量[13],因此,将向量ei参数化为
ei=[sinθicosφisinθisinφicosθi].
(6)
如图1所示,星号表示GEO卫星,α为GEO卫星至地球切线方向与卫星至地心方向的夹角;h为地心至地面距离;g为监测站;r为地球半径;θi为卫星与监测站分布面构成的圆锥顶角.

图1 GEO卫星定轨GDOP解算示意图
(7)
根据圆锥定位构型的GDOP最小值[14]可知,当满足以下2个条件时,GDOP值可以得到最小.
(8)
(9)
由于优于构型具有叠加不变性[14],因此将T层圆锥叠加,根据矩阵分块特性,N的逆矩阵可以表示为
(10)
i=1,2,3,…,T,T为嵌套圆锥数目.
因此,可建立目标函数:
(11)
式中:θi∈[0,α].
当式(11)达到最小的时候,即GDOP值最小.理论上,采用该监测站构型的定轨策略,会得到最优的GEO卫星定轨精度.
2 仿真实验分析
由式(11)可知,随着T的增加,嵌套圆锥构型分布存在无穷解.当顾及地球自转参数、模糊度、电离层延迟、对流层延迟等其他参数时,构型更为复杂.不同嵌套层数及同一嵌套圆锥上的不同监测站数量,也都会影响GDOP值的大小.本文以基础的2层嵌套圆锥为例进行仿真实验,以9个监测站,分别实验了1+8, 2+7, 3+6, 4+5策略的GDOP极值.
令:
M表明,θi(i=1,2,3,…)时,即监测站构型分布在GEO卫星下方时,目标函数取得较大值;L表明,θ1=θ2=θ3=…=θn,即当监测站分布在相近的圆锥上时,目标函数取得较大值.
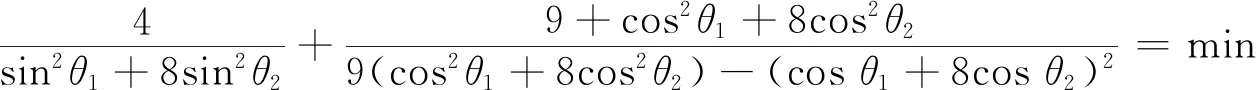
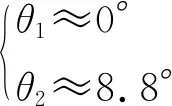
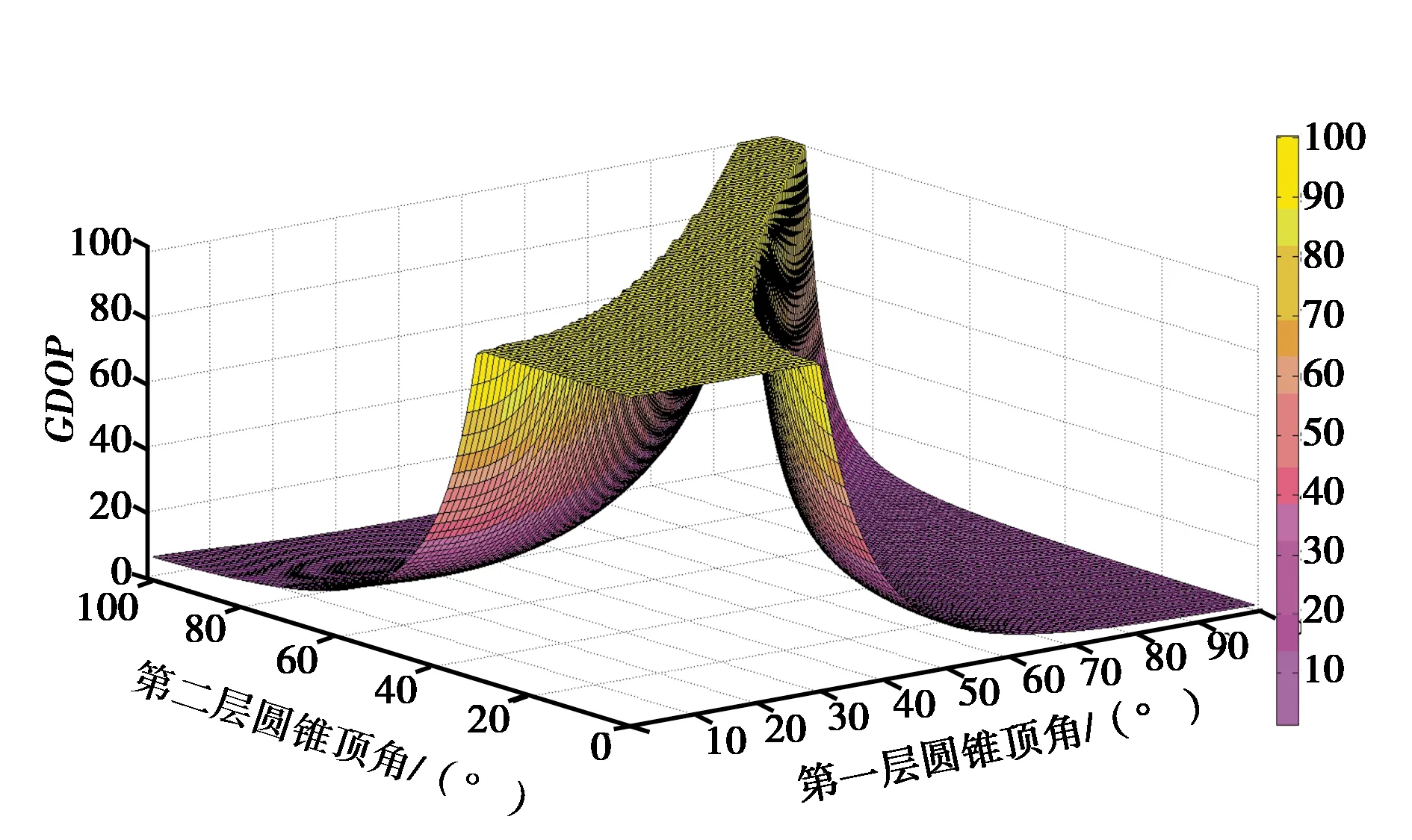
图2 2层嵌套(1+8)圆锥GDOP值仿真图
设T=2,n1=2,n2=7.则:
=min.
设T=2,n1=3,n2=6.则:
=min.
设T=2,n1=4,n2=5.则:
=min.
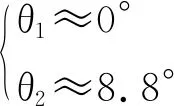
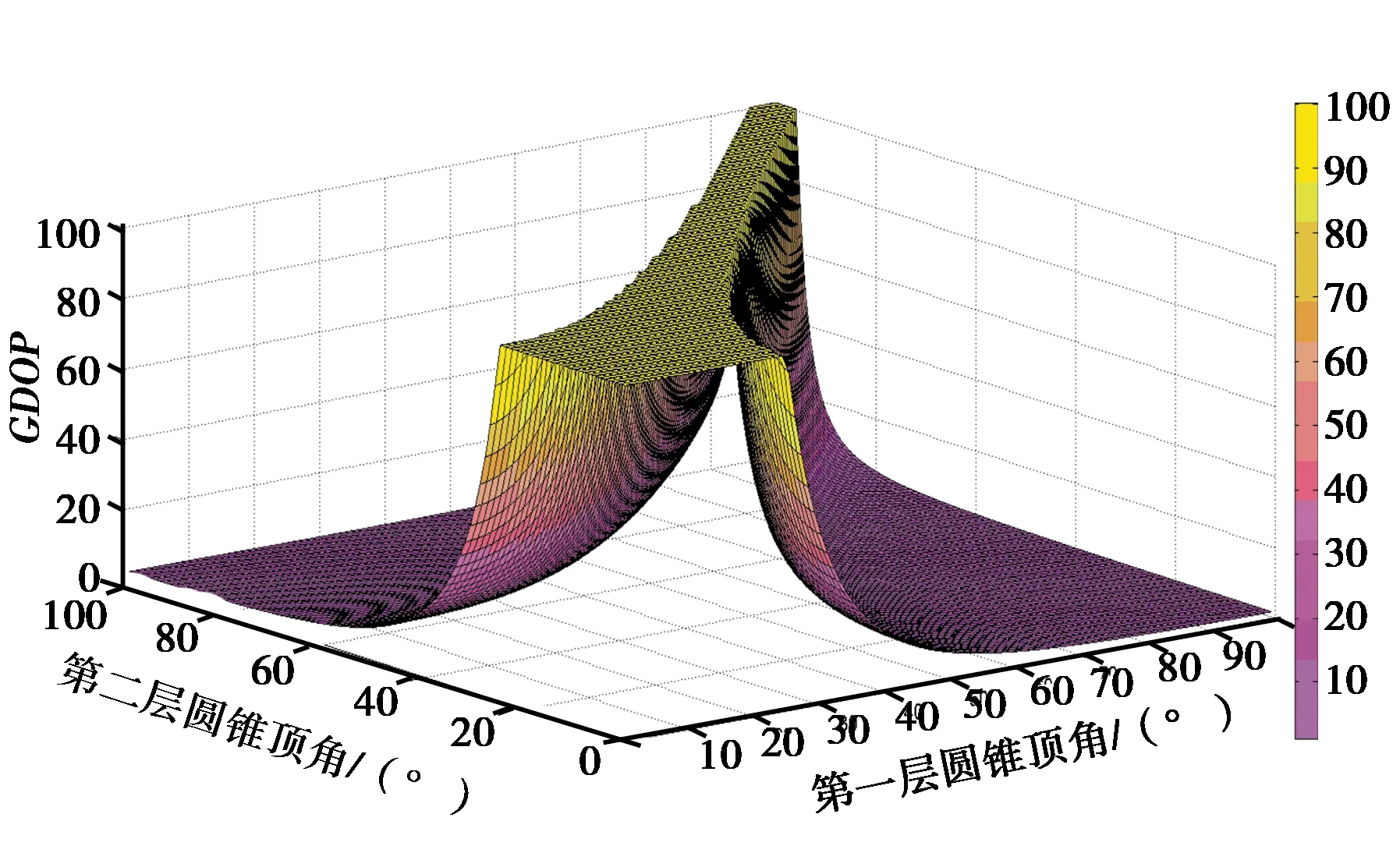
图3 其他3种2层嵌套圆锥GDOP值仿真图
3 结 论
本文基于卫星定轨的基本原理,采用嵌套圆锥构型,分析了测站构型对于GEO卫星定轨的影响,得到了一类理论上的不同测站构型的最优解,结论如下:
1)基于定轨精度因子,利用嵌套圆锥的构型方法,得到一类GEO卫星定轨的最优测站分布;
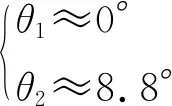
3)当嵌套圆锥数量不同(即监测站分布在多个面)、观测站数量越多时,最小GDOP值的构型越丰富;
4)本文方法可为导航卫星监测站布设提供依据,为顾及地球自转参数、模糊度、电离层延迟、对流层延迟等参数的GNSS精密定轨选站提供参考.
