北斗B1C信号联合捕获策略

吴涛, 唐小妹,马春江,吴健,孙广富

(国防科技大学 电子科学学院 导航与时空技术工程研究中心,湖南 长沙 410073)

0 引 言

随着卫星导航系统的发展,为了满足更高的性能需求,信号体制也随之更新换代. 其中,北斗三号(BDS-3)相对于北斗二号(BDS-2)的BPSK单通道信号体制,新增加的B1C信号采用了新型的QMBOC调制方式,传统的单一数据通道也改进为数据和导频双通道结构. 在城市建筑或其他物体遮挡的环境中,接收到的信号很微弱,相比于开阔地的接收信号,功率要低20～30 dB,只有-150～-160 dBm[1]. 此时,接收机为了能够捕获信号,需要尽可能延长相干积分时间以提高信噪比. 然而,传统信号单一的数据通道,调制了未知符号的电文,若相干积分时间过长,包含了电文比特翻转的边界,会使得相干积分的效果受到削弱. 新体制信号中加入了无电文调制的导频分量,理论上可以提升接收性能. 卫星导航信号需要满足一定的数据传输功能,除了导频通道,含有电文的数据通道也是必不可少的. 所以,新的信号体制具有数据和导频双通道结构.

如果只使用其中一个通道捕获,损失了另一通道的信号功率,必然导致检测性能下降. 所以现有文献主要研究了数据和导频通道的联合捕获算法,以提升接收性能. 联合捕获算法分为两类:一类是数据和导频通道等长相干积分联合算法,另一类是非等长相干积分联合算法.

等长相干积分联合算法,即数据和导频通道采用相等的相干积分时间. 文献[2-4]中,针对数据、导频通道功率比为1∶1的信号,推导了三种主要的等长相干积分联合检测量(非相干、相干和差分联合算法)统计特性的理论表达式,并对比了三者的性能,其中相干联合算法具有相对更优的性能. 但是上述研究没有考虑数据、导频非等功率的信号.

针对此问题,文献[5]在数据导频非等功率条件下,研究了加权的非相干联合算法,归纳了最优加权系数随检波输入信噪比、数据导频通道的功率配比变化规律;文献[6]在利用非相干联合算法捕获北斗B1C信号时,数据和导频通道检测量的加权系数设置为两通道的功率比值,与文献[5]提出的最优加权系数得到的性能差异还需对比研究;文献[7]在传统差分联合检测量的基础上,通过消除检测量中均值为零的噪声项的方法,提出了改进的差分联合检测量,并验证了其性能优于传统的三种检测量. 但是改进的差分联合检测量,忽略了B1C信号数据、导频通道的相对符号关系,而在实际中难以预知这一关系进行捕获.

另外,以上对等长相干积分联合算法的研究,还存在的问题是:导频通道与数据通道的相干积分时间相等,没有利用导频通道不含电文的特点,不能将导频通道上无电文的优势在信号捕获中发挥出来.

为发挥导频通道的优势,文献[8]在传统非相干联合算法的基础上,设计了非等长相干积分联合检测量,并推导得到统计特性的理论表达式,验证了非等长相干积分联合算法的性能随着导频功率比的增加而提升,性能能够优于非相干联合算法. 但是该文献将导频通道的相干积分时间设置为信号积分总时间. 若无多普勒频差,该处理方法是合理的;若考虑存在多普勒频率差带来的影响,文献[9-10]研究发现,此时存在最优的相干积分时间,导频通道的相干积分时间不应延长至信号总积分时间. 所以,还需对比等长与非等长相干积分联合算法,在不同场景条件下的性能差异,给出信号捕获可采取的最优策略.

为此,本文围绕北斗B1C信号,对三种等长相干积分联合算法的捕获性能进行深入分析,并比较等长与非等长相干积分联合算法的性能差异,目的是给出优化的捕获策略.

内容安排如下:第1部分介绍信号捕获模型,包括北斗B1C信号及捕获模型;第2部分介绍等长相干积分算法的原理及其性能对比;第3部分介绍非等长相干积分联合算法的原理及一般化模型;第4部分给出捕获参数设计方案,用于对比等长与非等长相干积分联合算法的性能,给出不同场景条件下捕获B1C信号的算法选择策略.

1 信号捕获模型

本部分首先介绍北斗B1C信号,包括基带和中频形式,然后介绍B1C信号的捕获模型.

1.1 信号模型

目前,北斗B1C信号参数如表1所示[11].

表1 B1C信号参数

北斗B1C信号的数据通道采用正弦BOC(1,1)调制,导频通道则采用了QMBOC调制;数据、导频通道的功率比为1∶3.

B1C基带信号可表示为

(1)

式中:ξD∶ξP11∶ξP61=11∶29∶4,表示各分量的功率比;d(t)为导航电文数据;cP2nd(t)为导频通道的次级码;cD(t)、cP(t)分别为数据、导频通道的伪码;c(t)·sc(t)表示利用方波副载波调制的信号,称为BOC信号;sc11(t)、sc61(t)表示两种频率的方波副载波,表达式为

sc11(t)=sign[sin(2πf11t)],

(2)

sc61(t)=sign[sin(2πf61t)].

(3)

式中:sign(·)为符号函数;f11=1.023 MHz,f61=6×1.023 MHz,分别对应BOC(1,1)和BOC(6,1)信号.

接收得到的B1C中频信号表达式如下:

cP(t-τ0)·sc61(t-τ0)]×

cP2nd(t-τ0)·cP(t-τ0)·sc11(t-τ0)×

sin[2π(fIF+fd)t+φ0]+nIF(t) .

(4)

1.2 捕获模型

捕获的目的是估计接收信号的载波频率与伪码相位,以实现载波与伪码的剥离,从中提取导航电文信息,同时伪码相位也是得到测距结果的重要信息.

B1C信号中的BOC(1,1)是窄带分量,BOC(6,1)是宽带分量. 当接收机选择宽带接收时,即选择接收所有的分量,功率利用率高,具有最优接收性能. 本文选择宽带接收方式捕获B1C信号.

接收机捕获导航信号的一般模型如图1所示，接收得到中频信号后,依次进行下变频、相关与相干积分,利用相干积分值构造检测量,然后进行非相干后积累,最终输入至捕获判决模块.

下面介绍相干积分、捕获判决的模型,其中相干积分表达式将体现下变频与相关的过程,检测量与联合捕获算法相关,将在下文第2、3部分进行分析.

图1 接收机信号捕获框图

1.2.1 相干积分

本地产生cD(t)·sc11(t)信号与rIF(t)相关,得到数据通道的相干积分值:

R11(Δτ)·cos(Δφ)+nD,I,

(5)

R11(Δτ)·[-sin(Δφ)]+nD,Q.

(6)

式中:ND=TD·fs,表示数据通道相干积分时间TD对应的采样点数; Δτ是本地伪码与接收信号伪码的码相位差;fe是本地载波与接收信号载波的频率差;R11(·)是BOC(1,1)信号自相关函数;Δφ是本地载波与接收信号载波相位差.

因为导频通道有两个分量,所以本地分别产生cP(t)·sc11(t)与cP(t)·sc61(t)两种信号与rIF(t)相关,得到四路相干积分值:

nP11,I,

(7)

nP11,Q,

(8)

nP61,I,

(9)

nP61,Q,

(10)

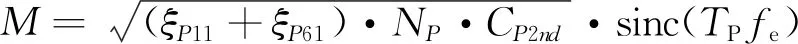
导频通道为QMBOC信号,文献[12]给出了适用于该类型信号的最佳匹配接收方式,得到整个导频通道的相干积分值如下:

=M·[ξP61·R61(Δτ)+ξP11·R11(Δτ)]×

cos(Δφ)+nP,I

RQMBOC(Δτ)·cos(Δφ)+nP,I,

(11)

=M·[ξP61·R61(Δτ)+ξP11·R11(Δτ)]×

sin(Δφ)+nP,Q

RQMBOC(Δτ)·sin(Δφ)+nP,Q.

(12)

当本地实现码相位正确匹配时,Δτ≈0,此时自相关值RQMBOC约为1.

1.2.2 捕获判决

利用等长或非等长相干积分联合算法,处理数据和导频通道的相干积分值构成检测量,对多个时段得到的检测量进行非相干后积累得到最终检测量V,输入至捕获判决.

假设H0表示被检测信号不存在,即接收信号只包含噪声;H1表示被检测信号存在,即接收信号同时包含被检测信号和噪声.

信号的捕获判决是根据检测量能否超过门限值得到的.当信号不存在时,检测量超过门限值,此时就造成了虚警;当信号存在时,且检测量能够超过门限值,那么此时就实现了正确的检测.虚警概率和检测概率可分别表示为

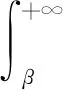
(13)

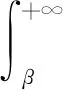
(14)

式中，β是判决门限. 一般采用恒虚警检测,即判决门限由虚警概率确定.

2 等长相干积分联合算法

目前研究的等长相干积分联合算法,主要有非相干、相干和差分联合算法三类. 由于B1C信号导频功率更高,导频通道的检测量应得到更高的加权,所以需要设计加权的联合检测量. 下面详细介绍这三种算法的加权联合检测量,并对比三者的捕获性能.

2.1 非相干联合算法

非相干联合(non-coherent combine)算法的检测量为

vnon=λnon·|vD|2+(1-λnon)·|vP|2.

(15)

当非相干后积累大于1时,检测量为

(16)

式中:vD=vD,I+jvD,Q,vP=vP,I+jvP,Q；λnon为非相干联合检测量的加权系数;k表示第k段的非相干联合检测量;K为总的后积累次数.

文献[5]分析发现,最优的加权系数与相干积分后的信噪比、数据导频通道功率相关. 对于B1C信号数据、导频通道的1∶3功率分配,最优加权系数的分布如图2所示.

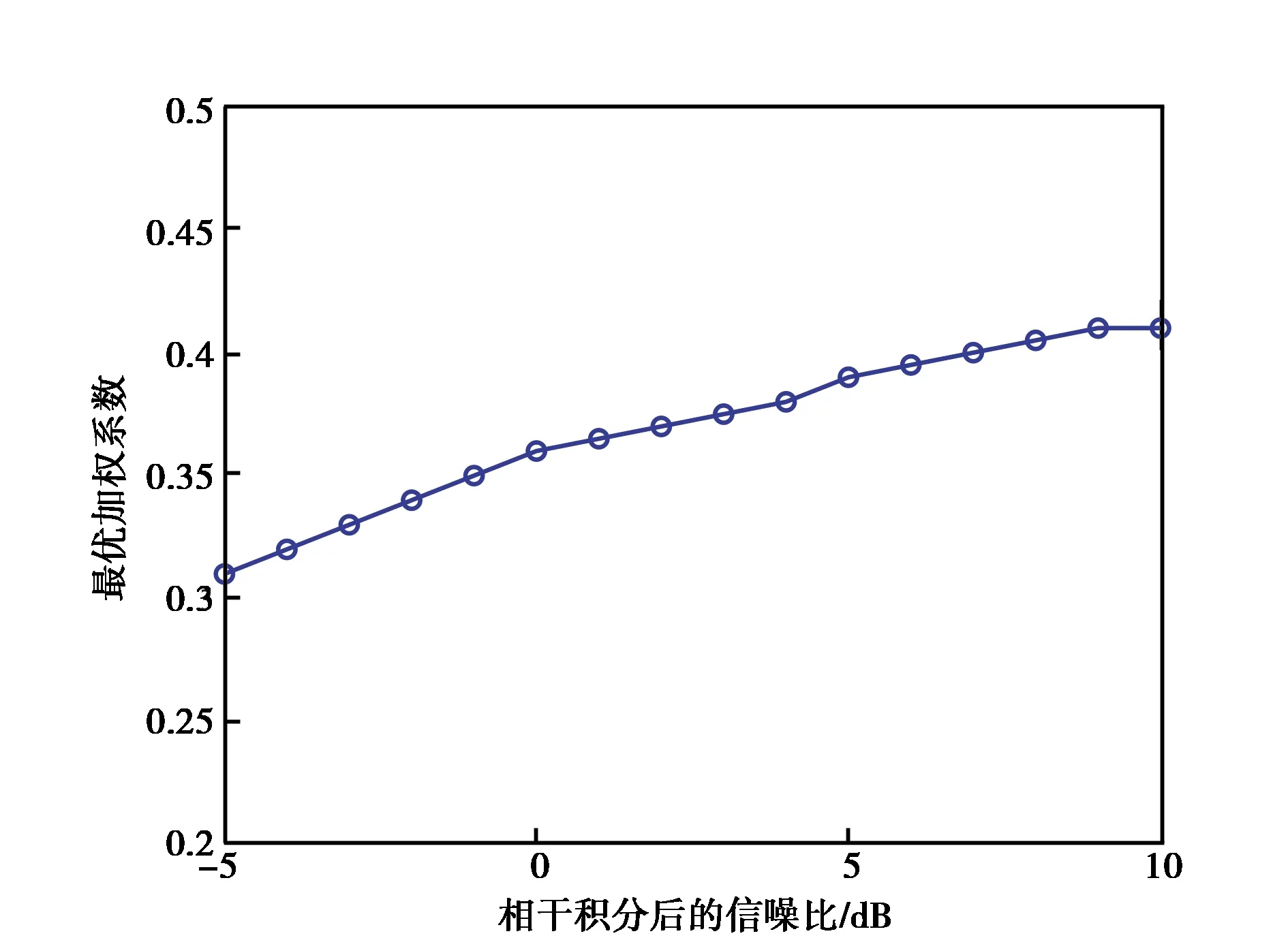
图2 非相干联合的最优加权系数

从图2中可以看出,最优加权系数随着相干积分后信噪比的增加而提高,当信噪比增大到10 dB以上时,此时最优加权系数约为0.4.

而文献[6]捕获B1C信号时,利用数据和导频通道的功率配比关系得到加权系数0.25. 下面分析加权系数0.25与最优加权系数的性能差异.

采用蒙特卡洛仿真方法,信号载噪比30～40 dB-Hz,相干积分时间为1 ms,可计算对应的相干积分后信噪比为0～10 dB. 根据图2选择近似的最优加权系数0.4,与加权系数0.25性能对比结果如图3所示.

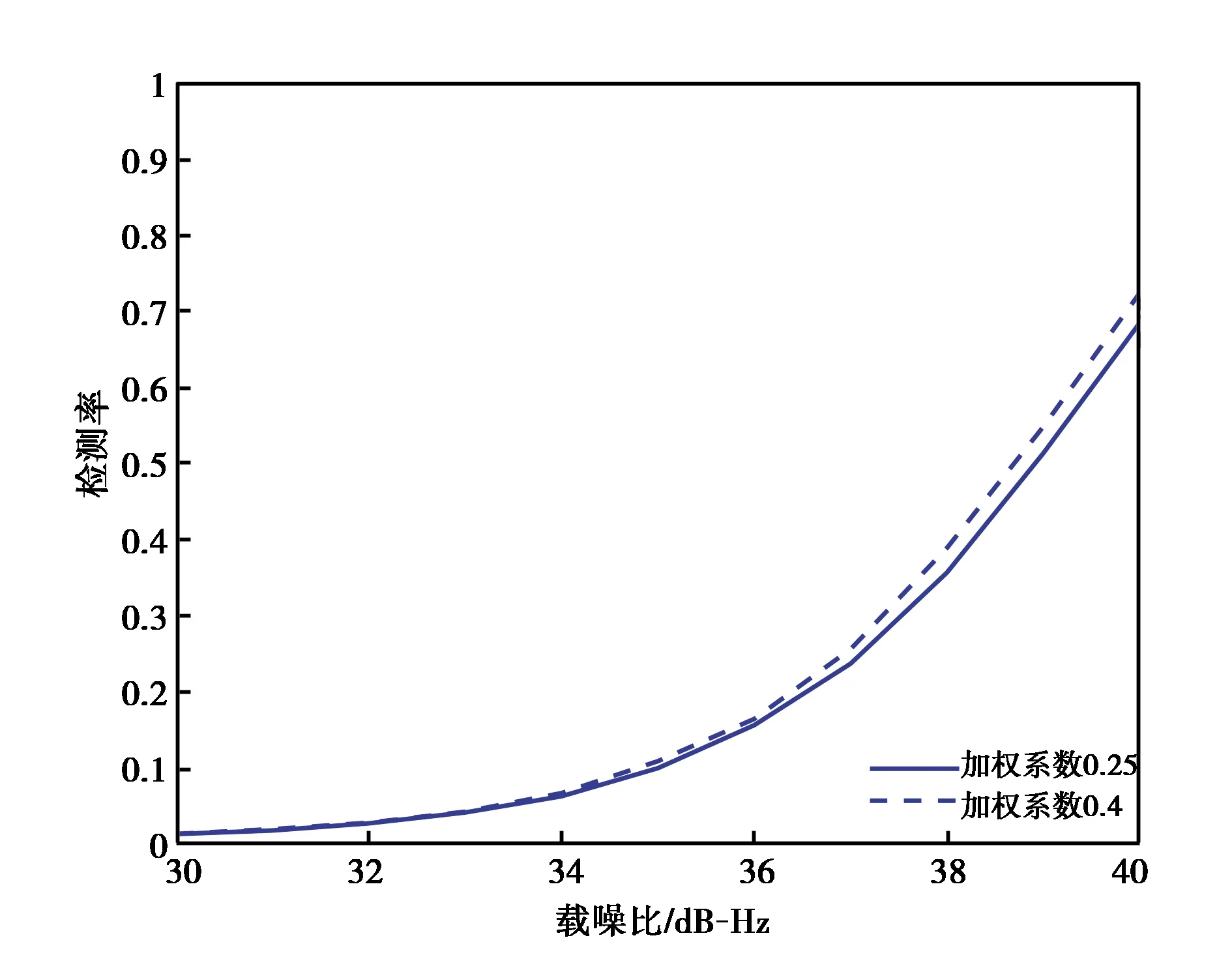
图3 加权系数0.25与0.4的性能对比

根据功率配比选择的加权系数0.25与最优加权系数的性能差异小于0.5 dB. 由于根据不同的相干积分信噪比选取最优加权系数较为繁琐,实际中捕获时根据功率配比选取加权系数的方案表现得更为简便.

2.2 相干联合算法

相干联合(coherent combine)算法的检测量为

vcoh=max{|v+|2,|v-|2},

(17)

(18)

(19)

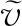
由于数据、导频通道分别存在未知符号电文和次级码,两者的相对符号关系未知,所以检测量的值存在以下两种可能性:

(20)

(21)

说明在H1条件下,|v+|2与|v-|2,一者服从中心χ2分布,另一者服从非中心χ2分布.

所以,相干联合算法的本质是估计数据、导频通道之间的相对符号.

数据、导频通道相关值幅度归一化后,根据式(5)～(6)、 (11)～(12)可知,方差关系从原来的4∶3变化为3∶1. 由式(20)、(21)判断,加权系数不改变均值的大小,v+与v-的方差相等,此时使得两者方差最小的加权系数即为最优加权系数,可用如下方法求得:

(22)

易知,最优加权系数λcoh=0.25,只与数据和导频通道的功率分配有关.

当非相干后积累次数大于1时,最终检测量为

(23)

因为数据和导频相对符号在各段相干积分的未知性,所以只能以非相干的方式对各段的相干联合检测量进行积累.

2.3 差分联合算法

文献[7]提出适用于B1C信号的差分联合(differential coherent combine)算法. 根据差分联合的原理,首先将数据通道与导频通道同相分量的复共轭相乘再取其实部,得到:

(24)

再将数据通道与导频通道正交分量的复共轭相乘再取其虚部,得到:

(25)

最后,对两个差分检测量加权后得到最终检测量:

vdiff=|λdiff·vdiff,I+(1-λdiff)·vdiff,Q|,

(26)

式(26)可改写为如下形式:

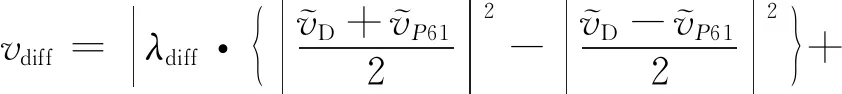
(27)

根据式 (27)可以发现,与相干联合检测量相同,差分联合检测量仍然受数据和导频通道相对符号关系的影响,当相对符号为+1时:

(28)

当相对符号为-1时:

(29)

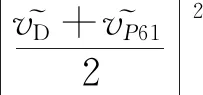
而文献[7]提出的改进差分联合检测量,忽略了相对符号的不确定性,将其当作确定量,从而省略差分检测量中均值为零的噪声项. 但是,若想改进差分检测量,需要对两种相对符号得到的检测量进行最大值的判决. 改进的差分联合检测量如下:

(30)

由于估计相对符号的原理与相干联合算法相同,改进后的差分检测量本质上与相干联合是等价的. 上述分析验证了差分联合算法不能优于相干联合检测量.

2.4 性能对比

采用蒙特卡洛仿真方式比较三种算法的检测性能. 仿真参数如下:相干积分时间1 ms(无特殊性,数据和导频通道的相干积分时间相等即可);非相干后积累次数选取1、5次;给定虚警率为10-3. 得到检测性能曲线如图4所示.

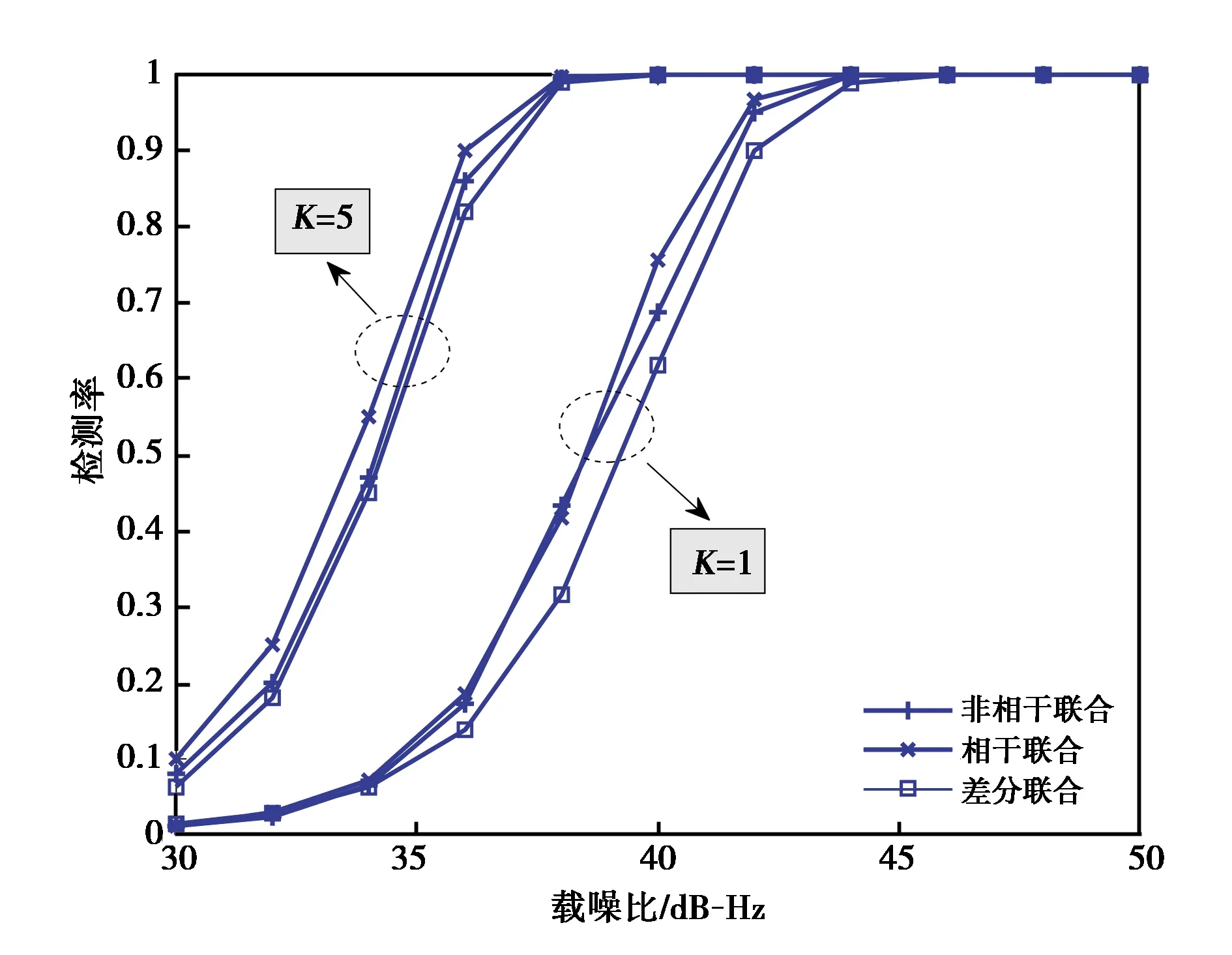
图4 等长相干积分联合算法的性能对比

图4说明:非相干后积累次数无论是1次还是大于1次,在三种等长相干积分联合算法中,相干联合算法均表现出更优的性能.

3 非等长相干积分联合算法

非等长相干(unequal length coherent)积分联合算法,由于两通道的相干积分时间不相等,所以对应的非相干后积累次数不同. 数据、导频通道的检测量分别为

(31)

式中:k1、k2分别表示数据、导频通道的第k1、k2段相干积分值;K1、K2为两者的后积累次数.

最终的联合检测量只能采用非相干联合的方式得到,其一般化的检测量模型为

Vuc=λuc·VD+(1-λuc)·VP,

(32)

式中,λuc为加权系数. 加权系数与两通道功率比、积分参数有关,难以得到显性的理论关系式,所以可以采用遍历λuc∈(0,1)得到优化的加权系数.

同时可以发现,非等长相干积分联合算法其实是基于等长积分非相干联合算法的变换.

4 捕获参数与算法选择策略

实际工程中存在两种情况:

1) 信号总积分时间给定,计算最优相干积分时间及其对应的非相干后积累分段数,给出检测性能;

2) 检测性能指标给定,计算最优相干积分时间及所需的信号总积分时间.

由于本文研究的是等长与非等长相干积分联合算法的性能及策略选择,所以采用给定信号总积分时间的约束条件,比较两种算法的检测性能.

4.1 捕获参数的设计

结合第2、3部分的分析,本部分首先利用最优相干积分时间理论,提供捕获参数的设计方案. 其中,相干积分时间及其非相干后积累次数是需要设计的重要参数.

若相干积分时间过短,那么在信号载噪比较低时,非相干积分的输入信噪比过低,会导致较大的检波损耗;若相干积分时间过长,会受到多普勒频率差的影响,导致较大的频率损耗,削弱相干积分增益.

文献[9-10]分析发现,对于利用相干积分与非相干后积累结合的捕获方法,存在最优的相干积分时间使得处理损耗最小. 以B1C信号导频通道为例,经过相干积分后的信噪比为

(33)

经过非相干后积累以后总的近似损耗为

(34)

式(34)说明损耗与载噪比、频率差、相干积分时间有关. 在给定信号载噪比、频率差的条件下,可用以上公式计算出最优的相干积分时间. 易知,随着载噪比和多普勒频差的增加,最优相干积分时间逐渐降低.

得到最优相干积分时间后,在给定信号总积分时间的条件下,相应地可确定非相干后积累的分段数. 为保证分段数为整数,本文提出如下的捕获参数设计方案:相干积分时间应选择最优值附近的近似值,能整除总积分时间. 例如,当载噪比为40 dB-Hz,频率差为50 Hz时,此时理论最优的相干积分时间为3 ms. 那么实际捕获中,若信号总积分时间为10 ms,可选择近似值2.5 ms作为相干积分时间,分段数为4次.

数据与导频通道的参数差异在于,数据通道在捕获阶段,相干积分时间一般不超过电文长度的一半,对于B1C信号即5 ms[1],以保证每两段相干积分值中必然有一段不受电文符号翻转的影响. 当最优相干积分时间大于5 ms时,导频通道可采用相对更长的积分时间;而小于5 ms时,两通道应采用等长的积分时间.

4.2 联合算法的选择策略

根据4.1节中的参数设计方案可知,5 ms相干积分时间是两种联合捕获算法性能的临界值.

约束信号载噪比范围为20～40 dB-Hz,选取4种多普勒频率差,利用式(34)计算出最优相干积分时间,其中存在与5 ms相近的最优相干积分时间. 如图5所示.

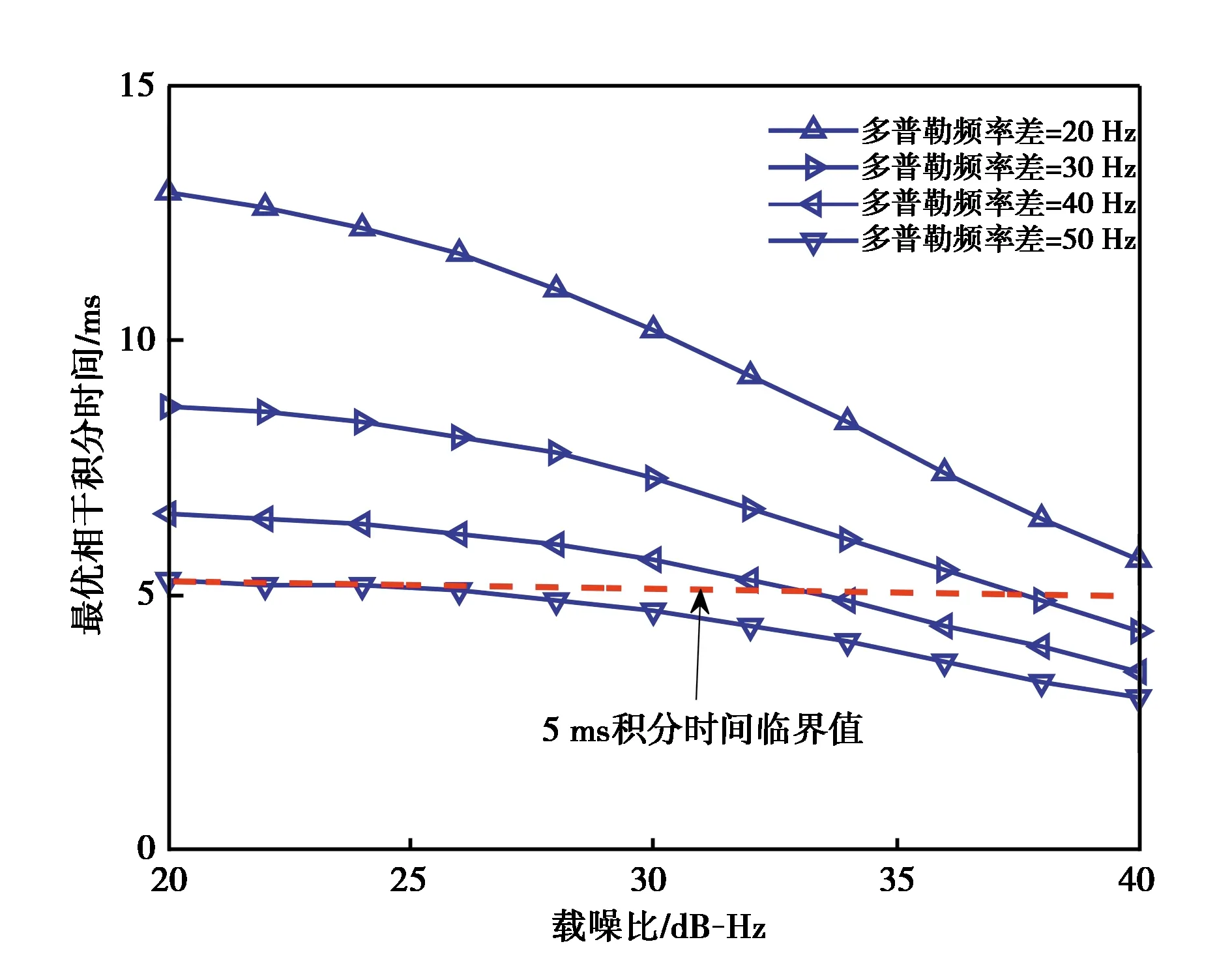
图5 不同多普勒频率差对应的最优相干积分时间

图5表明,当信号载噪比为20～40 dB-Hz时,多普勒频率差若大于50 Hz,数据和导频通道最优相干积分时间将不超过5 ms,此时应选择相干联合算法;若多普勒频率差为30～40 Hz,存在信号载噪比临界值以决定捕获算法的选择;多普勒频率差若小于20 Hz,导频通道最优相干积分时间可超过5 ms,此时非等长相干积分联合算法性能将更优.

下面采用蒙特卡洛仿真方法验证上述分析.给定虚警率为10-3,信号载噪比为20～40 dB-Hz,多普勒频率值分别取20、30、40、50 Hz. 信号总积分时间选取10 ms和20 ms进行比较,对应的捕获参数近似值则利用4.1节的设计方案进行选取. 得到检测性能曲线如图6所示.

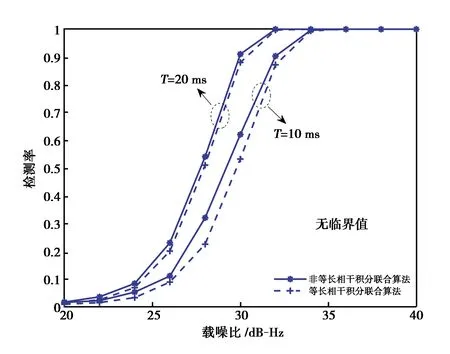
(a) 多普勒频率差20 Hz

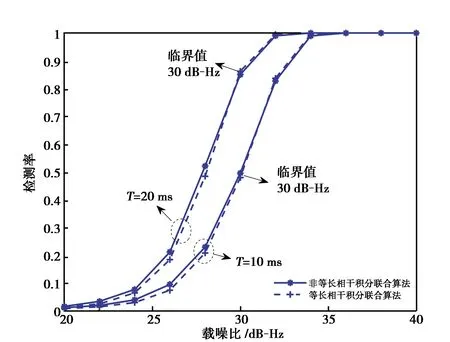
(b) 多普勒频率差30 Hz

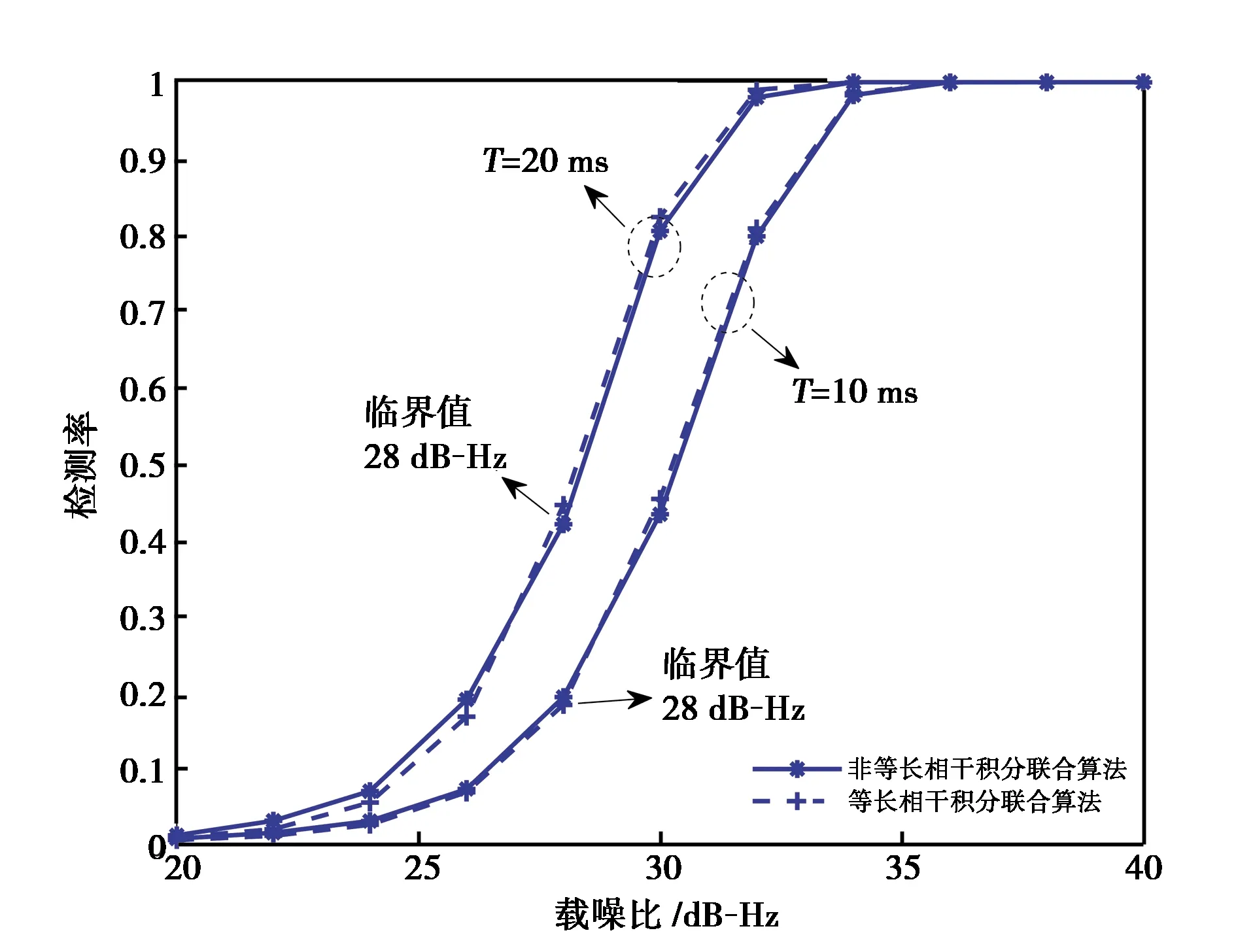
(c) 多普勒频率差40 Hz

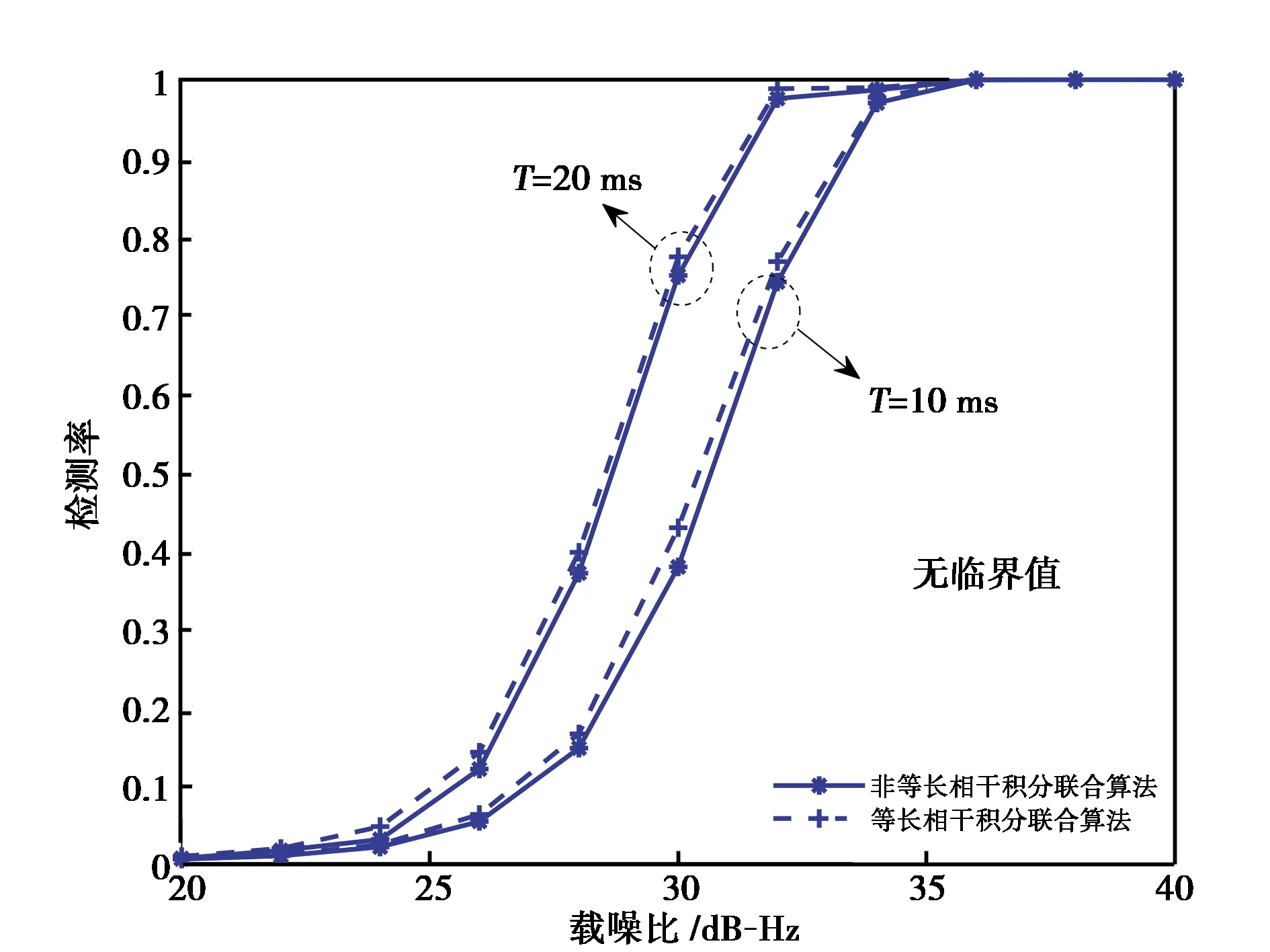
(d) 多普勒频率差50 Hz图6 等长与非等长相干积分联合算法的性能对比

根据图6的仿真结果,整理得到B1C信号捕获算法的选择策略如表2所示.

表2 B1C信号捕获算法的选择策略

在信号载噪比为20～40 dB-Hz的条件下,根据理论与仿真结果可得到B1C联合捕获算法选择策略为:当多普勒频率差小于20 Hz时,非等长相干积分联合算法具有更优性能;当多普勒频率差为30 Hz时,两种算法的载噪比临界值约为30 dB-Hz;当多普勒频率差为40 Hz时,两种算法的载噪比临界值约为28 dB-Hz;当多普勒频率差大于50 Hz时,选择相干联合算法性能更优.

5 结束语

本文围绕B1C信号的联合捕获问题,首先对三种等长相干积分联合算法展开深入分析,讨论了加权系数的问题,并解释了相干联合优于差分联合算法的内在机理,通过蒙特卡洛仿真验证相干联合具有更优的性能.

进一步,利用最优相干积分时间的理论,给出捕获参数设计方案. 在总积分时间相等的条件下,利用设计方案选择捕获参数,对比等长与非等长相干积分联合捕获算法的检测性能,给出算法选择策略. 通过理论分析和仿真验证,得到联合捕获算法选择策略为:在信号载噪比20～40 dB-Hz的条件下,当多普勒频率差小于20 Hz时,非等长相干积分联合算法具有更优性能;当多普勒频率差为30 Hz、40 Hz时,选择两种算法的载噪比临界值为30 dB-Hz、28 dB-Hz;当多普勒频率差大于50 Hz时,相干联合算法更优.

本文提供了捕获参数设计及联合捕获算法选择的方法. 实际工程中,可利用最优相干积分时间理论,根据实际的输入条件选择捕获参数与算法.