实现不围棋博弈程序的一种策略及关键算法

2020-09-18陈雪健张利群曹杨

现代计算机 2020年22期

陈雪健，张利群，曹杨

（辽宁石油化工大学计算机与通信工程学院，抚顺 113001）

0 引言

近年来，中国大学生计算机博弈大赛暨中国计算机博弈锦标赛开展得越来越好，主要表现在两个方面，一个是参加大赛的高校代表队越来越多，另一个是竞赛棋种越来越多，截止到2019 年，比赛棋种达到19 种。

在中国大学生计算机博弈大赛暨中国计算机博弈锦标赛中，不围棋是在2012 年引入的竞赛棋种，当年共有8 个代表队参加不围棋的比赛[1-4]。2019 年的中国大学生计算机博弈大赛暨中国计算机博弈锦标赛中共有12 个代表队参加不围棋的比赛，可见大学生对不围棋的参与度不高，原因是多方面的，其一是对不围棋的研究文献极少，可借鉴的内容不多，其次与不围棋本身具有的特点有重要关系，那就是行子策略复杂、棋局的复杂度高以及行子可行性判定算法实现困难[5-10]，这些特点限制了许多大学生组队参赛。本文介绍了不围棋博弈程序实现过程中的一种策略以及着法可行性的判定算法。

不围棋（No Go）也是国际计算机奥林匹克竞赛棋种，其棋盘、棋子和棋规定义如下。

（1）棋盘

不围棋棋盘同九路围棋棋盘，即9×9 围棋的棋盘，如图1 所示。

图1 不围棋棋盘

（2）棋子

黑、白两色围棋棋子。

（3）棋规

①黑子先手，双方轮流落子，落子后棋子不可移动；

②吃子：一个棋子在棋盘上，与它直线紧邻的空点是这个棋子的“气”。棋子直线紧邻的点上，如果有同色棋子存在，则它们便相互连接成一个不可分割的整体，它们的气也应一并计算。棋子直线紧邻的点上，如果有异色棋子存在，这口气就不复存在。如所有的气均为对方所占据，便呈无气状态，无气状态的棋子不能在棋盘上存在，应当提出盘外。当一方落子，使得对方的棋子为无气状态，就是吃子。

③对弈的目标不是吃掉对方的棋子，不是占领地盘，恰恰相反，如果一方落子后吃掉了对方的棋子，则落子一方判负；

④对弈禁止自杀，落子自杀一方判负；

⑤对弈禁止空手（pass），空手一方判负；

⑥每方用时15 分钟，超时判负；

⑦对弈结果只有胜负，没有和棋。

1 一种行棋的策略

从不围棋的棋规中可以看出，对弈的目标不是吃掉对方的棋子，不是占领地盘，取胜的关键是谁最后有位置可行棋，谁最后取得胜利。

虽然占领地盘大小不决定胜负，但是从实战经验来看，往往占用地盘多且眼多的一方在收官阶段行棋的位置就多一些，获胜的概率就大一些，因此在自己成眼的同时，破坏对方成眼，逼迫对方眼少，最终使对方无处可走，直至输棋。为阐述方便，所有图示当中，以黑子代表我方，白子代表对手方。在实现不围棋计算机博弈程序时，策略有很多，以下是自己采用的一种策略。

1.1 先占角、再占边，最后占中间

在不围棋的行子过程中，构成眼最少用两子，就是角，其次是边，最后是中间，如图2 所示。

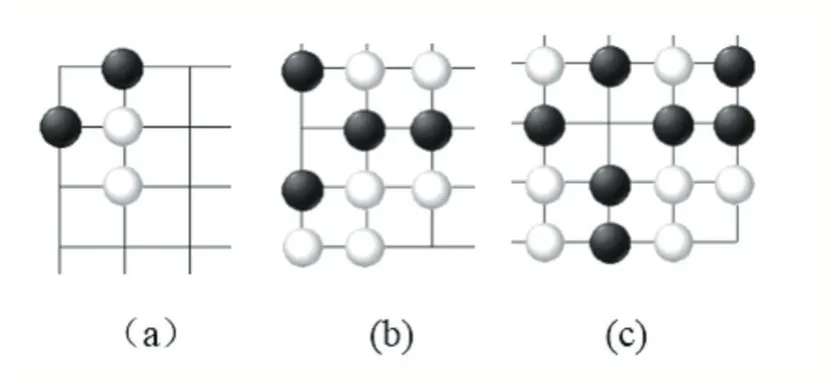
图2 三种类型的眼

事实上，由于不围棋棋规要求，即使构成上述眼的情况，确实限定了对方在眼处行棋，但是自己将来也不一定能在自己构成的眼处行棋，还要看周边的情况，也就是气的情况，这也是行棋过程中要注意的地方。

如图3 所示，黑方眼的位置，黑方自己也不可以行棋，因为行棋就是自杀棋。

图3 黑方无法在自己眼处行棋

最好将两个以上的眼连在一起，也就是围棋的做活，迫使对方在自己的眼处无法行棋，而自己在收官阶段，由于有两个眼，至少还有两口气在，就能在自己的眼处行棋，如图4 所示。

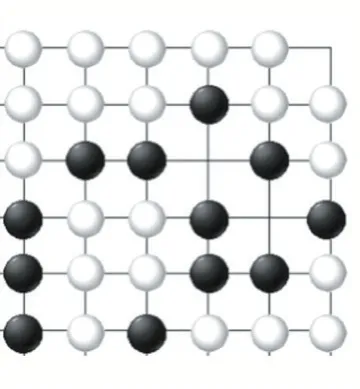
图4 在黑方眼处可以行一个黑子

1.2 攻击对手的策略

在对弈过程中，要极力破坏对手眼的形成，最好在行棋过程中既能自己形成眼，又能破坏对方眼的形成，这是最佳策略。在破坏对方成眼时，重点考虑如下几种情况，形成提前预判。由于各种情况的种类较多，这里仅举几个代表性的示例。

（1）行一子，欲形成四个眼，如图5 所示。

图5 行一子欲形成四个眼

（2）行一子，欲形成三个眼。

（3）行一子，欲形成两个眼，如图6 所示。

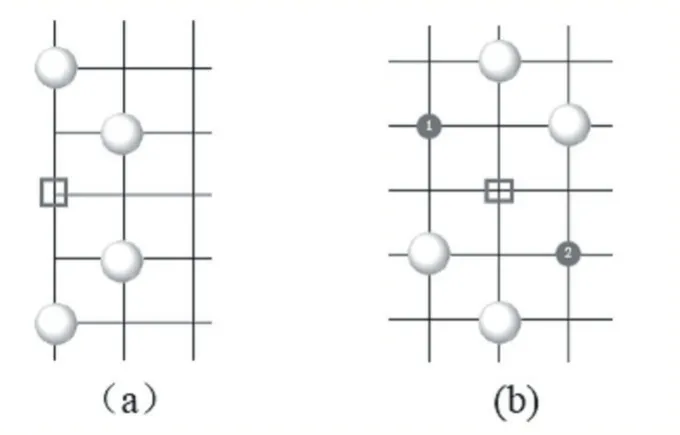
图6 行一子欲形成两个眼

（4）行一子，欲形成一个眼。

在行棋过程中，还要尽可能不让对方棋子做活，这样即使对方形成了单眼也无法在单眼处行棋。

2 不围棋的存储结构

针对不围棋棋盘行和列的特点，其棋盘的物理存储结构可以采用二维数组来表示，用C 语言描述如下：

int b[9][9];

不围棋就有黑白两种棋子，可以将黑子和白子分别用1 和2 来表示。

假设目前棋局如图7 所示，在计算机存储时，用二维数组表示如下：

图7 棋局状态图

b[0][0]～b[0][8]:0，2，0，1，0，1，0，1，0

b[1][0]～b[1][8]:1，0，2，2，0，0，1，0，2

b[2][0]～b[2][8]:0，2，0，2，0，0，0，0，0

b[3][0]～b[3][8]:0，0，1，0，0，0，0，0，0

b[4][0]～b[4][8]:0，0，0，0，1，0，0，0，0

b[5][0]～b[5][8]:0，0，0，0，0，0，0，0，0

b[6][0]～b[6][8]:0，0，0，0，0，0，0，0，0

b[7][0]～b[7][8]:1，0，0，0，0，0，2，0，1

b[8][0]～b[8][8]:0，2，0，0，0，0，2，1，0

也就是，棋盘上行棋位置有黑子的值是1，有白子的值是2，无子的位置为0。

后面算法需要将上述二维数组的位置存储到一个栈中，这就需要将二维坐标（i，j）转化为一维坐标k，转换方法如下：

k=i*9+j

反过来，将存储起来的一维坐标k 转换为二维坐标（i，j）的方法如下：

i=k∕9

j=k%9

3 着法可行性算法

在不围棋的“机-机”博弈过程中，对弈双方交替行棋，按照棋规，在行子过程中不能吃对方棋子，也不能自杀，因此，我方在某个位置准备行棋，就要判断该位置是否可以行棋，即要判断在这个位置行棋之后，是否我方连成一片的棋子有气，同时还要判断与我方行棋处邻接的对方棋子是否有气。

3.1 同色邻接棋子位置入栈递归函数

为了能够判断在b[i][j]处我方落黑子之后，是否吃掉了对方棋子，就要看这个黑子邻接的白子是否有气，没有气就是吃子了，如图8 所示，假设b[i][j]为b[5][3]。

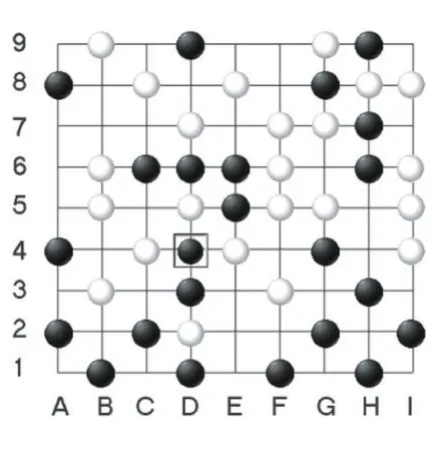
图8 黑子行棋位置

如何判断邻接的白子是否有气？这就需要把与黑子邻接的上下左右四个方向的白子块，存储起来，再计算其气数，只要有一个白子块的气数为零，则说明吃子发生了，这样我方在这个b[i][j]处就不能行棋。判断黑棋是否是自杀，道理与这个相同，不再赘述。用于存储白子块、黑子块的线性表如下，采用的是栈的存储方式[11-14]。

int wstack[81]，wtop=-1;

int bstack[81]，btop=-1;

采用深度优先算法将所有邻接的白子所在位置全部存储在一维数组wstack 中，且存储过程中，每一位置都不重复存储。函数int Isunique（int x）用于判定位置x 是否在栈中出现，若出现函数值为0，否则函数值为1，函数 Isunique（int x）实现简单，在此略去。

邻接白棋子的位置入栈递归函数如下：

与（i，j）处邻接的黑子入栈函数，与函数Adwpush（）的类型及参数一致，可参照函数Adwpush（）实现，不妨叫做 Adbpush（）。

3.2 气的计算算法

把邻接的白子块存储在了栈wstack[]中，该白子块是否有气，只需检查白子块中每个棋子的上下左右是否有空位置，只要有一个白色棋子邻接一个空位置，这个白子块就有气。

计算白子块气的算法如图9 所示，称之为Haswqi（）算法，返回值是1，就代表有气，算法返回值是0，就代表无气。

对于邻接b[i][j]的黑子，只有一个黑子块，其气的计算算法与此类似，不再赘述，称之为Hasbqi（）算法。

图9 Haswqi（）算法

3.3 着法可行性判定算法

有了上述算法，就可以给出我方在b[i][j]处着法可行性判定算法，如图10 所示。若在b[i][j]处可行棋，算法返回值为1，不可行棋，算法返回值为0。

当我方要在b[i][j]处行子，根据i、j 的值，最多需要判断四个白子块的气，这四个白子块是分别从b[i-1][j]、b[i+1][j]、b[i][j-1]及 b[i][j+1]处进行深度优先遍历得到的。其中Initwstack（）是白子块栈初始化函数，Initb⁃stack（）是黑子块栈初始化函数。