考虑最优转子动能的风电场自适应频率控制策略

杨立滨， 宗 鸣， 李春来

（沈阳工业大学 电气工程学院， 辽宁 沈阳 110870）

0 引言

风力发电通过电力电子型变流器并网运行，风电机组的有功功率与系统频率处于解耦状态，不具备常规火电机组的惯性和一次调频能力。 当大规模风力发电代替传统火电机组接入电网时会降低整个电网的惯性，且电网的一次调频能力有所弱化。在未来高渗透率风电并网运行的趋势下，电力系统的频率安全稳定问题面临着较大的挑

战[1]～[4]。

目前，风电机组的频率控制主要集中在转子动能和备用功率控制两方面。 在风电机组转子动能控制方面，其基本思想是将存储在风电机组的旋转动能转换为电磁功率，从而模拟同步发电机的惯性响应能力，在功率缺额瞬间能够释放该部分转子动能来响应电网的频率变化[5]～[7]。然而上述研究没有考虑合理利用风电场的可释放转子动能，会造成风电场转子动能的浪费，使得风电机组的惯性响应和一次调频能力难以得到有效的利用。在备用功率控制方面，其基本思想是控制风电机组处于减载运行，预留一部分的有功功率来响应电网频率的变化[8]～[10]。 实现风电机组备用功率控制的主要方法有转子转速控制和桨距角控制，该类方法通常在风电机组转子侧有功控制环增加一次调频下垂控制器，参与电网的频率控制。 然而该方法未考虑风电场内风电机组的控制特性，仅采用固定的下垂增益不能合理、充分地利用风电机组的备用功率。

本文提出了一种考虑最优转子动能的风电场自适应频率控制策略。在相同减载水平下，通过建立风电机组转子动能的优化模型， 最大化地利用风电场可释放的转子动能； 同时采用变下垂增益实现风电机组的一次调频功能， 有效地改善了系统的频率调节性能。最后，在PSCAD/EMTDC 仿真软件中建立大型风电场并网仿真模型， 对所提的控制策略进行了验证。

1 风电机组转子动能优化模型

1.1 风力机模型

变速恒频风电机组因其在机组结构、 控制方法等方面的灵活性和优势， 逐渐成为目前的主流风力发电机组。以双馈风电机组为例，主要由风力机、发电机以及全功率变流器等组成。双馈风力发电机组的数学模型为[11]

式中：Pm为双馈风力发电机组的输出机械功率；ρ为空气密度；A 为风力机风轮的扫风面积；VW为输入风速；Cp为风能利用系数；β 为风力机的桨距角；λ 为风力发电机组的叶尖速比； 系数c1=0.517，c2=116，c3=0.4，c4=5，c5=21，c6=0.006。

双馈风力发电机组的有功功率控制基本原理框图如图1 所示。 其控制系统主要包括风力机转速控制和桨距角控制，其中：风力机组控制系统的参考值主要为有功功率Pref以及桨距角β；而背靠背全功率变流器主要分为机侧变流器和网侧变流器， 机侧变流器的控制目标是风力发电机的输出功率， 网侧变流器的控制目标是变流器的直流侧电压和风力发电机的无功功率； 变流器控制系统均采用PI 控制。

图1 双馈风电机组有功控制基本原理Fig.1 Basic principle of active power control for doubly fed wind turbine

1.2 转子动能优化模型

对于双馈风电机组而言， 其转子转速和电网频率处于解耦状态，不能响应电网频率的变化。双馈风电机组的转子转速运行范围较宽， 能够存储大量的转子动能， 且能够通过附加控制来参与电网频率调节。为使风电场参与电网频率调节，通常使其处于减载运行，从而留有一定的备用容量。

依据风电机组的不同运行工况，风电机组可通过控制转子转速和桨距角实现减载运行[12]，从而使其运行在最优叶尖速比，也可使得风电机组转子动能达到最大。其中转子动能的大小可表示为

式中：J 为风电机组的转动惯量；ωr0为风电机组的初始转子转速。

风电机组的最大转子动能可表示为

实际风电场受尾流效应影响， 下游风机的实际输入风速低于上游风机[13]。 考虑尾流效应影响的下游风机的实际输入风速可表示为

式中：Vi为第i 台风电机组的输入风速；V0为自然风速；aj为第j 台风电机组的轴向感应系数；Dj为第j 台风电机组扫过面积的直径；k 为常数；xij为辐射距；βij为遮挡系数。

在尾流效应作用下， 风电场内每台风电机组的实际输入风速存在差异性， 在执行风电场频率调节时同样可以通过优化求解出风电场的最优转子动能， 即在相同的减载量下风电场能够输出更多的转子动能。 假设风电场的风电机组输入风速为Vw，i，根据风电机组有功运行曲线，能够求得该风电机组的最优转速ωopt，i以及最大运行有功功率Pmppt，i，且假设在优化算法控制后的风电机组转速和桨距角分别为ωdel，i，βi，则风电机组转子动能优化模型的目标函数可表示为

式中：ΔEk，i为第i 台风电机组的转子动能；N 为风电机组的数量；ωdel，i为第i 台风机降载运行时的转速；ωopt，i为第i 台风机最优转子转速。

式（7）优化的变量是风力发电机的转子转速，使其运行在转子旋转动能的最大运行点上。 由此可知， 当风电场内每台风电机组的输入风速不同时，在执行相同的减载水平下，能够找到风电场内各个风电机组转子旋转动能总和最大的运行点。

另外从约束条件来看， 风电场总的降载功率等于各台风电机组降载功率之和， 且各台风电机组的转子转速、桨距角、转子动能和降载功率均在规定范围之内。 对应的约束条件为

式中：ΔPd为风电场总的降载功率；ΔPd，i为第i台风电机组的降载功率；Pmppt，i为第i 台风电机组的最大运行有功功率；Pdel，i为第i 台风电机组的降载运行有功功率；βmin和βmax分别为风机桨距角的最小值和最大值；ΔEk，min和ΔEk，max分别为风电机组 转 子 动 能 的 最 小 值 和 最 大 值；ΔPd，min和ΔPd，max分别为风电机组降载功率的最小值和最大值。

2 风电机组变下垂控制方法

2.1 下垂参数整定方法

根据风电机组转子动能优化模型能够确定风电机组的降载运行点， 在此基础上本文制定了双馈风电机组下垂参数整定方法。

风电机组频率控制一般采用下垂控制策略，其基本目标是当电网频率发生变化时， 能够为系统提供一定的有功支撑。 图2 为传统的风电机组有功-频率下垂控制原理框图，其控制过程如下：

式中：iqref为风电变流器的有功电流参考值；kp和ki分别为PI 控制器的参数；Pref为风电机组的有功功率参考值；Rw为有功频率下垂控制系数；fref为电网频率参考值；fsys为检测到的电网频率。

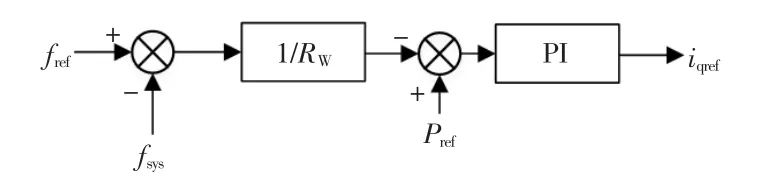
图2 风电机组有功-频率下垂控制Fig.2 Active-frequency droop control of wind turbine

风电场各台风电机组在相同减载水平下，系统频率的提升效果与风电场可释放的有功备用大小相关， 其中风电机组参与一次调频的备用功率通常包含转子动能和减载功率。 而风电机组的有功备用与一次调频下垂增益参数相关， 在相同减载水平下， 上游输入风速较大的风电机组通常具备更多的转子动能和减载功率， 因此上游风电机组的下垂增益可设置大一些，反之，下游风电机组设置较小的下垂增益。 设风电机组转子动能所转换的有功功率为

式中：Pi（ΔEk，i）为第i 台风电机组转子动能转换的有功功率。

则风电场的备用功率可表示为

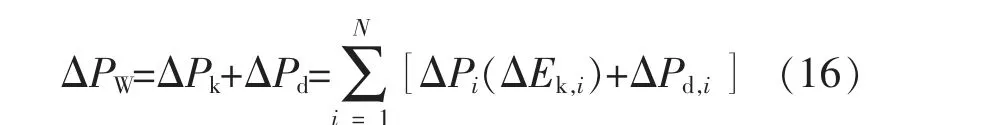
风电机组一次调频的下垂增益的整定原则是依据风电机组当前的备用功率。 当风电机组可释放的备用功率较大时， 其一次调频下垂增益可设置大一些；而当可释放的备用功率较小时，则设置较小的一次调频下垂增益。

2.2 变下垂控制方法

基于上述分析， 变下垂增益控制方法的原理框图如图3 所示。

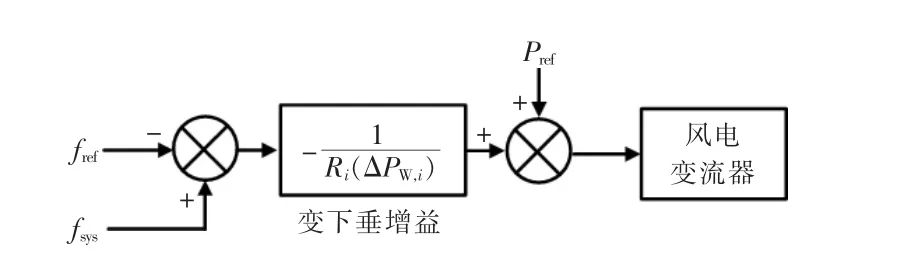
图3 风电机组变下垂控制方法Fig.3 Variable droop control method of wind turbine

变下垂控制环的有功电流输出可以定义为

为了获得更好的频率调节性能并确保稳定工作， 根据当前的备用容量来设定风电机组的变下垂增益，具体为

式中：RW，i为第i 台风电机组的变下垂增益；C 为常系数。

3 算例分析

为验证本文所提风电场自适应频率控制策略的正确性， 在PSCAD/EMTDC 软件中建立如图4所示的大型风电场仿真模型， 其中风电机组转子动能优化模型通过Matlab 软件编程进行求解。 风电场含有3 条集电线路， 每条集电线路上接有4个风电机组，每个风电机组容量为2 MW。 为了区分每列风电机组， 分别对不同集电线路上的风电机组的每列进行了编号。风电机组基本参数如下：容量为3 MV·A，机端电压为0.69 kV，惯性时间常数为5 s，风电机组变压器变比为0.69 kV∶10 kV。输电线路变压器变比为10 kV∶110 kV；系统负荷容量为100 MW。 本文分别采用风速不变以及风速时变两种场景进行算例验证。

图4 风电场仿真模型Fig.4 Simulation model of wind farm

（1）算例1：风速不变

假设仿真系统输入风速不变， 仿真中在第5秒投入一定的有功负荷， 系统由于有功功率缺额而发生频率跌落。 将本文所提频率控制策略与风电场不采取频率控制、 传统固定下垂增益的频率控制策略的控制效果进行了对比。 首先根据风电场站内不同风电机组的输入风速， 分别对每列风电机组的备用功率和下垂控制增益进行计算，系统频率响应和风电场有功功率响应结果分别如图5，6 所示。 本文所提频率控制策略和传统固定下垂增益的频率控制策略的减载水平相同。

图6 风电场有功响应曲线Fig.6 Active power response curve of wind farm

由仿真结果可知： 当风电机组不采取频率控制策略时， 在功率缺额瞬间会发生较大的频率偏移，频率最低值为49.76 Hz；当采用固定下垂控制策略时， 在频率跌落瞬间能够进行风电场的有功调节，但是由于没有合理利用风电场的转子动能，无法在系统频率跌落时进行有效的频率支撑，频率最低值为49.83 Hz； 本文所提控制策略由于充分利用了风电场以及每台风电机组的转子动能，能够在系统频率跌落瞬间释放更多的转子动能，且在频率响应过程中提供了更多的有功支撑，因而具备更好的一次调频能力，频率最低值为49.86 Hz。 相较于传统固定下垂控制策略，文中所提控制策略在相同减载水平下的最低点频率有效提升了0.03 Hz。

（2）算例2：风速时变

为了验证本文所提控制策略在实时风况下的频率控制效果， 选取我国某风电场实测风速数据拟合曲线作为实时输入风速， 风速曲线如图7 所示，仿真场景同算例1。 将本文所提控制策略和采用固定下垂增益的频率控制策略进行了仿真对比，仿真结果分别如图8，9 所示。

图7 实时风速曲线Fig.7 Real time wind speed curve

图8 风速时变下的系统频率响应曲线Fig.8 Frequency response curve of system with time-varying wind speed

图9 风速时变下的风电场有功响应曲线Fig.9 Active power response curve of wind farm with timevarying wind speed

由仿真结果可以看出， 在实时风速变化工况下，相较于传统的固定增益下垂控制策略，本文所提控制策略在相同减载水平下能够最有效地利用风电场的转子动能， 从而输出更多的有功功率来响应系统的频率变化， 使系统的频率波动范围以及有功变化波动都更小， 表现出更好的频率支撑性能。

4 结论

①风电机组最优转子动能优化模型通过协调转子转速和桨距角来控制风电机组的转子转速，使其在相同减载水平下具有更多的可释放转子动能， 从而具有更多的备用功率来响应系统频率变化。

②建立风电机组一次调频下垂增益和当前备用功率大小的函数关系， 输入风速大的风电机组因具有更多的备用功率而设置更大的下垂增益，而输入风速小的风电机组则设置更小的下垂增益。

③本文所提控制策略相较于传统的固定下垂增益的风电场一次调频控制策略， 能够更加充分地利用风电场的转子动能， 从而具有更好的一次调频控制性能。