关于光伏电池最佳风冷方案的模拟研究

2020-09-17郭玮，刘杰

可再生能源 2020年9期

郭玮，刘杰

（青岛理工大学环境与市政工程学院，山东青岛 266033）

0 引言

目前，光伏电池的发电效率仍然较低，这限制了光伏电池的发展[1]。标准测试条件下，常用的硅太阳能电池的发电效率只有12%～17%。与标准测试条件下相比，实际工作条件下，硅太阳能电池的发电效率降低了20%以上[2]。影响光伏电池发电效率的因素有很多，如光伏电池温度、晶体结构、光谱范围、负载阻抗和阴影遮挡等。其中，光伏电池温度是影响自身发电效率的主要因素之一[3]，[4]。有关研究表明，光伏电池温度每升高1 ℃，光伏电池输出功率约降低0.4%[5]。因此，为了提高光伏电池的发电效率，有必要对光伏电池进行冷却。

常见的光伏电池冷却方式有风冷方式和水冷方式。近年来，随着科技的进步，兴起了一些新型冷却技术（热管冷却、热电冷却等）[6]。从传热的角度看，当光伏电池采用水冷方式时，由于水具有较大的比热容，因此，光伏电池的散热效果较好，但是水冷系统管路复杂，存在介质泄漏和低温凝固等隐患[7]。当光伏电池采用风冷方式时，光伏电池与空气直接进行对流换热，与水冷系统相比，风冷系统中空气通道的施工更加方便，且该系统无液体介质泄露的风险[8]。新型冷却技术尚不成熟，还处于研究阶段，应用案例较少。因此，光伏电池的风冷系统成为国内外学者们的研究热点。 Mazón-Hernández 研究分析了空气通道截面、空气流速和面板温度对太阳能电池板电压、电流和输出功率等电学参数的影响，但在风冷通道强制对流研究过程中，没有考虑风机功率的影响[9]。邓鹏杰在光伏电池风冷通道中增加了翅片，实验结果表明，增加翅片后，能够增强光伏电池的冷却效果，并提高其发电性能，但翅片结构增加了冷却系统的复杂程度，也增加了施工难度和系统初始投资[10]。

本文基于光伏建筑一体化技术，以提高光伏电池发电效率为目的，以冷却系统结构简单、冷却效果有效为原则，设计了3 种易于实现的光伏电池风冷散热结构，这3 种结构充分考虑了风机耗功对光伏电池输出性能的影响，并利用Fluent 仿真模拟软件对光伏电池的风冷结构进行了优化计算，最终得到了最佳的光伏电池风冷方案。

1 计算模型

1.1 模型建立

图1 为3 种光伏电池风冷结构的示意图。本文以3 块光伏电池为一组，分别建立风冷模型并对其进行模拟计算。 3 种散热结构均主要由空气通道、光伏电池和导流板3 部分组成，不同之处在于导流板的位置。每组光伏电池朝向均为正南，背面均安装了长方体空气通道，空气由空气通道的下侧流入、上侧流出。每个光伏电池面板的几何尺寸为1 200 mm×600 mm，空气通道的几何尺寸为1 200 mm×1 844 mm×w（w 为通道宽度），导流板的几何尺寸为1 200 mm×30 mm×22 mm。图中：vin为空气通道进口速度；vout为空气通道出口风速。光伏电池侧的导流板既起到导流作用，又能够将光伏电池固定在建筑表面上，光伏电池侧导流板的位置固定不变；空气通道侧的导流板仅起到导流作用，通过调整该导流板在竖直方向上的位置改变空气的流向。

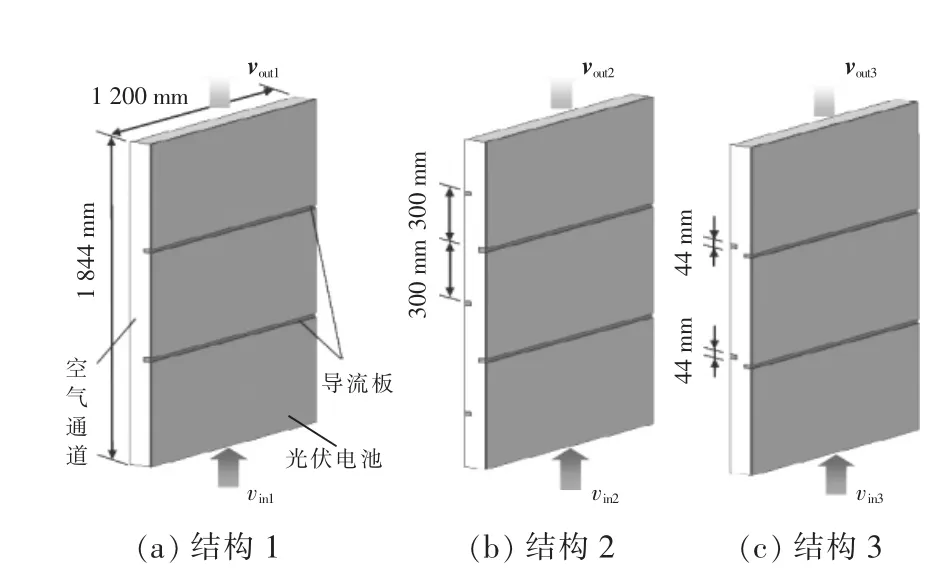
图1 3 种光伏电池风冷结构示意图Fig.1 Schematic diagram of three types of air-cooling structures for photovoltaic cells

由图1 可知：结构1 仅在光伏电池侧布置了2 块导流板，分别位于3 块光伏电池的连接处，起到扰流作用；结构2 布置了5 块导流板，其中，2块导流板位于光伏电池侧，位置与结构一相同，另外3 块导流板位于空气流道侧，其中，1 块导流板位于空气流道的中间，其他2 块导流板与空气流道中间的导流板之间的距离均为300 mm；结构3布置了4 块导流板，光伏电池侧的2 块导流板在竖直方向比空气流道侧导流板略低了44 mm，以形成冲刷光伏电池面板的空气流向。

当光伏电池发电时，会有一部分太阳能转化为热能。这些热能一部分通过对流换热的方式散失到环境中，另一部分传递至空气通道，被流道内的空气所吸收。

本文在模拟过程中对光伏电池进行了结构简化，只考虑了2 层透明面板以及光伏电池片。简化后，环境侧透明面板、光伏电池片和空气通道侧透明面板的厚度分别为3.20，0.75，3.00 mm。

1.2 模拟方法及边界条件

本文基于Fluent 软件进行模拟计算。利用Fluent 软件自带的能量方程、湍流模型进行自然对流和强制对流的模拟计算。本文使用Gambit 软件建立三维模型，采用结构化网格对模型进行网格划分，选择Fluent5/6 求解器进行计算。

在自然对流模型的计算过程中，须开启重力项和浮力项，并采用Boussinesq 假设。空气进口为压力进口边界，空气出口为压力出口边界。在强制对流模型的计算过程时，空气进口为速度进口边界，空气出口为压力出口边界。其他边界条件的设置：环境空气温度为303.15 K；环境侧透明面板与空气进行对流换热，对流换热系数为8 W/（m2·K）。根据测试数据可知，12：00，太阳辐照度为500 W/m2，此时光伏电池的光电转化效率约为10%，即大约10%的太阳辐射能被转化为电能，此外，大约10%的太能辐射能被反射，大约80%的太能辐射能（400 W/m2）转化为热能。本文将这部分热能作为光伏电池的内热源加载到模型中进行计算。

根据测试数据可知，当光伏电池平均温度T0为323.15 K 时，3 块光伏电池串联后的输出功率为110 W。以自然对流条件下光伏电池平均温度为基准，按照光伏电池温度每升高1 ℃，光伏电池输出功率降低0.4%进行计算[5]。当光伏电池工作温度为T 时，3 块光伏电池串联后的输出功率WT与光伏电池工作温度T 的线性关系式为

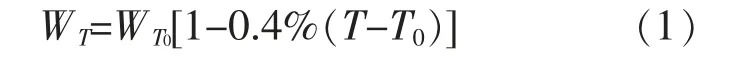
式中：T0为光伏电池的平均温度，取323.15 K；WT0为T0条件下，光伏电池的输出功率，W。

根据自然对流条件下的模拟结果可知，在不同空气通道宽度w 下，光伏电池的平均温度为337～337.4 K。本文取337 K 作为光伏电池的基准温度，则该条件下光伏电池的输出功率WT=337K为103.9 W。强制对流条件下的光伏电池输出功率与自然对流情况下光伏电池输出功率的增量△W为

实际工况下，强制对流须要消耗一定的引风机功率。引风机功率△P 的计算式为

我与王述金是在2005年相识的，那年，我到他家去调查巫音，申报省、市非遗保护名录。我说：“沮水巫音有可能被列为国家级非遗保护名录，说不定还能代表保康，出国表演呢？”六十多岁的王述金，听我这么一说，开心得像个孩子。没想到这句话，他却牢牢地扎在心里。

式中：V˙为引风机的体积流量，m3/s.

因此，强制对流带来的净发电功率增量为△WT与△P 的差值。

1.3 模拟验证

本文将模拟结果与实验结果进行对比，以验证模拟的可靠性。实验系统的示意图见图2。

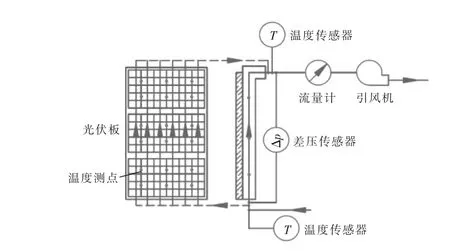
图2 实验装置系统图Fig.2 System diagram of the experimental setup

实验过程中，利用引风机抽取环境空气，使空气从底部流入空气通道，并与光伏电池进行对流换热，然后从顶部流出。本文在空气通道进、出口截面几何中心处分别布置了热电偶，以测量空气进、出口处的温度；在透光面板表面上均匀布置了18 个热电偶测点，以测量透光面板的温度；在空气通道内均匀布置了9 个测点（3×3），以测量空气通道内空气的平均温度。引风机的流量可以调整，本文利用流量计测量空气流道的空气流量，利用压差计测量空气流道的进、出口压力差，从而计算出引风机的功率。

实验过程中，空气通道的宽度为30 cm，其他几何尺寸与图1（a）相同。空气流道的进口温度为环境温度（306.55 K），出口流速为4.75 m/s。测量时间为12：20-15：20，太阳辐照强度为462.32 W/m2。

根据测量结果和模拟结果可知，透光面板平均温度的测量值为325.55 K，模拟值为329.75 K，模拟误差约为8%；空气通道内空气平均温度的测量值为307.95 K，模拟值为308.65 K，模拟误差约为2%。综上可知，模拟误差均在8%以内，因此本文模型模拟结果的准确性较高。透光面板平均温度的模拟值比实验值略高，这是由于模拟过程中忽略了接触热阻和内部细微结构（胶膜等）热阻而造成的。此外，实际测试过程中，散热结构侧表面保温层不可能达到绝热状态，尤其是在室外环境相关参数波动剧烈（环境风速波动等）的情况下，会对透光面板温度产生极大影响。

2 模拟结果及分析

图3 为当空气通道宽度为6 cm 时，3 种散热结构的光伏电池的平均温度随空气通道进口速度的变化情况。

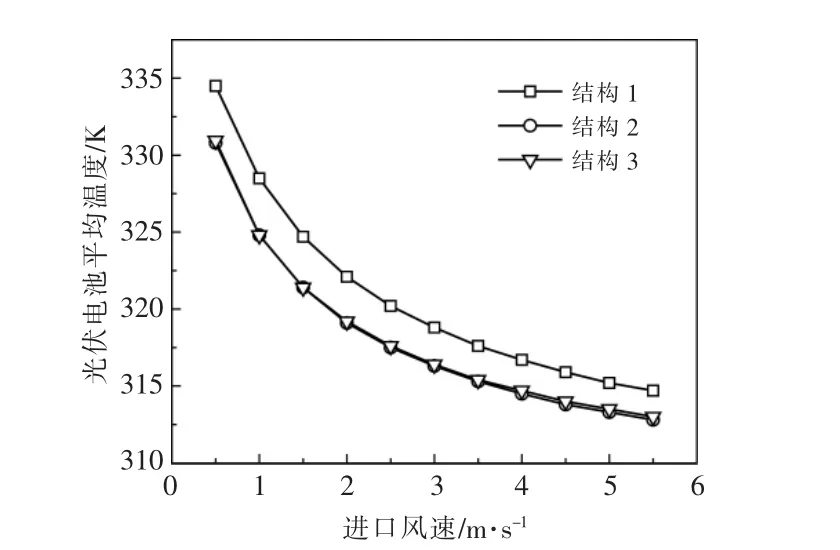
图3 3 种散热结构光伏电池的平均温度随空气通道进口速度的变化情况Fig.3 Temperature variation of photovoltaic cells of three types of air-cooling structures with air inlet velocity

由图3 可知：随着空气通道进口速度逐渐增大，光伏电池平均温度逐渐降低，且降低速度逐渐减小，这是由于随着空气通道进口风速逐渐增大，光伏电池与空气之间的对流换热不断增强，但是，当风速大于5 m/s 时，空气通道内的换热强度逐渐趋于极限，因此，光伏电池平均温度的降低速度逐渐减小。

图4 为当光伏电池风冷结构（以下简称为风冷结构）为结构1 时，不同空气通道宽度w 条件下，光伏电池平均温度随空气通道进口速度的变化情况。

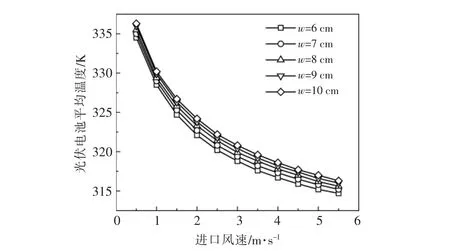
图4 风冷结构为结构一时，不同w 条件下，光伏电池平均温度随空气通道进口速度的变化情况Fig.4 Temperature variation of photovoltaic cells with air inlet velocity in structure 1 with different w

由图4 可知，随着空气通道进口速度逐渐增大，光伏电池平均温度逐渐降低，且降低速度逐渐减小。当空气通道进口速度由0.5m/s 逐渐增大至2.5m/s 时，光伏电池平均温度迅速降低，约降低了14 K；当空气通道进口速度由2.5 m/s 逐渐增大至5.5m/s 时，光伏电池平均温度仅降低了约6 K。由图4 还可看出，随着空气通道宽度逐渐减小，光伏电池平均温度也逐渐降低。当空气通道宽度由10 cm 逐渐减小至6 cm 时，同一空气通道进口速度下，光伏电池的平均温度降低1.6～2.1 K。

综上可知，增加空气通道进口速度、减小空气通道宽度均可以获得光伏电池板温度降低的有益效果，从而可以提高光伏电池的发电效率，但是同时也会增加引风机的功率。

图5 为当风冷结构为结构1 时，不同空气通道宽度条件下，引风机功率ΔP 与光伏电池发电功率增量ΔW 随空气通道进口速度的变化情况。图中：ΔP11～ΔP15分别为空气通道宽度为6～10 cm时，引风机的功率；ΔW11～ΔW15分别为空气通道宽度为6～10 cm 时，光伏电池发电功率的增量。

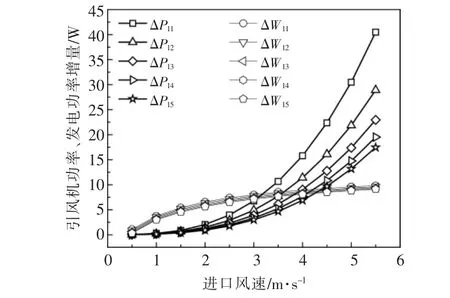
图5 当风冷结构为结构1 时，不同w 条件下，引风机功率和光伏电池发电功率增量随空气通道进口速度的变化情况Fig.5 The variation of power generation increase of photovoltaic cells and power consumption of fan with air inlet velocity in structure 1 with different w

由图5 可知，引风机功率和光伏电池发电功率增量均随着空气通道进口速度的增加而增加，但引风机功率的增速先慢后快，光伏电池发电功率增量的增速先快后慢，因此引风机功率曲线和光伏电池发电功率增量曲线存在交点。交点处，引风机功率和光伏电池发电功率增量相等。在相同空气通道宽度条件下，当空气通道进口速度小于发电功率增量曲线与引风机功率曲线交点处所对应的空气通道进口速度时，光伏电池发电功率增量大于引风机功率，则系统发电功率净增量（光伏电池发电功率增量与引风机功率之差）为正；反之，当空气通道进口速度大于光伏电池发电功率增量曲线与引风机功率曲线交点处所对应的空气通道进口速度时，光伏电池发电功率增量小于引风机功率，系统净发电功率为负。由图5 还可看出：不同空气通道宽度条件下，光伏电池发电功率增量变化很小，这说明空气通道宽度对光伏电池发电功率增量影响较小；空气通道宽度对引风机功率的影响随空气通道进口速度的增加而增大。此外，空气通道宽度越小，使得系统发电功率净增量为正值的空气通道进口速度的变化范围越小，因此，针对不同的散热结构，应确保空气通道进口速度在合理范围内，从而使系统发电功率净增量为正值。

图6 为当风冷结构为结构1 时，不同空气通道宽度条件下，系统发电功率净增量随空气通道进口速度的变化情况。

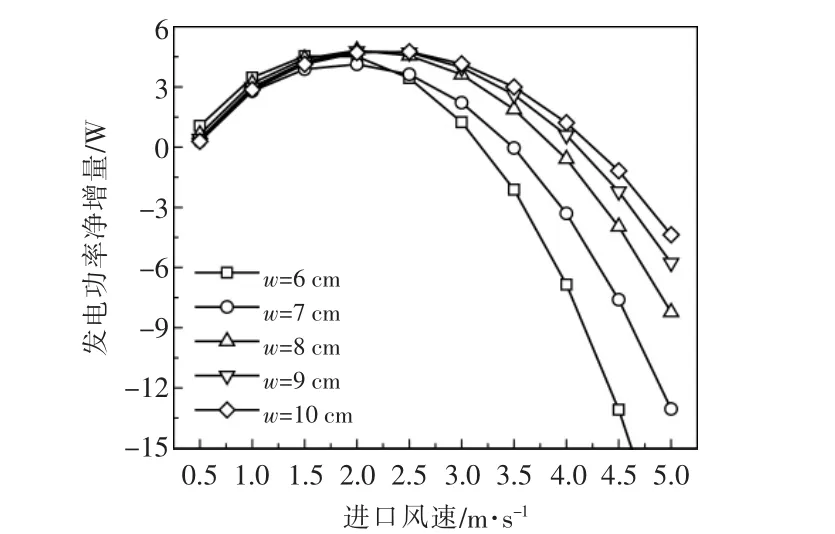
图6 当风冷结构为结构1 时，不同w 条件下，系统发电功率净增量随空气通道进口速度的变化情况Fig.6 The variation of net power generation increase with air inlet velocity in structure 1 with different w

由图6 可见，随着空气通道进口速度逐渐增大，系统发电功率净增量呈现出先增大后减小的变化趋势，使得系统发电功率净增量为正值的空气通道进口速度变化范围随着空气通道宽度的增大而增大。当空气通道宽度为6，10 cm 时，使得系统发电功率净增量为正值的空气通道进口速度分别为0.5～3.2 m/s 和0.5～4.3 m/s。由图6 还可看出，当风冷结构为结构1 时，空气通道的宽度宜选取8～10 cm，可以获得较大的系统发电功率净增量，在此条件下，与自然对流条件下光伏电池的输出功率相比，当空气通道进口速度为1.75～2.25 m/s 时，光伏电池输出功率至少增加4.30%。

图7 为当风冷结构为结构2 时，不同空气通道宽度条件下，系统发电功率净增量随空气通道进口速度的变化情况。

由图6，7 可知，当风冷结构为结构2 时，系统发电功率净增量随空气通道进口速度的变化趋势与结构1 时相同，但使系统发电功率净增量为正值的空气通道进口速度变化范围整体上有所减小。由图7 可知，当空气通道宽度为6，10 cm 时，使得系统发电功率净增量为正值的空气通道进口速度分别为0.5～2.1 m/s 和0.5～2.8 m/s。当空气通道宽度为6 cm 时，空气通道进口速度宜选取0.75～1.25 m/s，与自然对流条件相比，该空气通道进口速度条件下，光伏电池输出功率至少增加了3.45%；当空气通道宽度为8～10 cm 时，空气通道进口速度宜选取1.25～1.75 m/s，与自然对流条件相比，该空气通道进口速度条件下，光伏电池输出功率至少增加了3.78%。

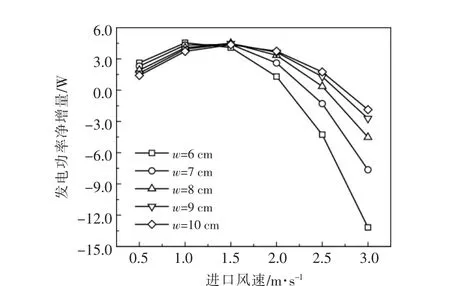
图7 当风冷结构为结构2 时，不同w 条件下，系统发电功率净增量随空气通道进口速度的变化情况Fig.7 The variation of net power generation increase with air inlet velocity in xtructure 2 with different w

图8 为当风冷结构为结构3 时，不同空气通道宽度条件下，系统发电功率净增量随空气通道进口速度的变化情况。

图8 当风冷结构为结构3 时，不同w 条件下，系统发电功率净增量随空气通道进口速度的变化情况Fig.8 The variation of net power generation increase with air inlet velocity in structure 3 with different w

由图6～8 可知，当风冷结构为结构3 时，系统发电功率净增量随空气通道进口速度的变化趋势与风冷结构为结构1，2 时相同，但在结构3 条件下，使系统发电功率净增量为正值的空气通道进口速度变化范围整体上小于结构1，2。由图8可知，当空气通道宽度为6，10 cm 时，使得系统发电功率净增量为正值的空气通道进口速度分别为0.5～1.7 m/s 和0.5～2.3 m/s。当空气通道宽度为6～9 cm 时，空气通道进口速度宜选取0.75～1.25 m/s，与自然对流条件相比，该空气通道进口速度条件下，光伏电池输出功率至少增加了2.80%；当空气通道宽度为10 cm 时，空气通道进口速度宜选取1.25～1.75 m/s，与自然对流条件相比，该空气通道进口速度条件下，光伏电池输出功率至少增加了2.98%。