计及备用容量的光伏发电系统等比例减载调频控制技术研究
2020-09-17王利猛孙珮然许成哲姜鸿儒
王利猛, 孙珮然, 韩 凯, 许成哲, 姜鸿儒
(1. 东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室, 吉林 吉林 132012; 2.国网吉林省电力公司长春供电公司, 吉林 长春 130000; 3. 国网山东省电力公司费县供电公司, 山东 临沂273400)
0 引言
近年,光伏(Photovoltaic, PV)、风电等可再生能源被广泛应用。 由于PV 系统通常在最大功率点(Maximum Power Point, MPP)运行,不能向电网提供惯性响应或频率响应[1]~[3],因此,相关规定明确要求可再生能源发电机组必须具备一定的电网调 频能力[4],[5]。
在PV 系统的研究领域内,文献[6]提出了一种无任何储能装置的光伏-柴油混合调频策略,但其需要光照数据和复杂的控制系统来实现。 文献[7],[8]采用离线拟合和在线跟踪相结合的方式提高减载控制的容错性,在此过程中,其可以与现有最大功率跟踪方法无缝融合, 进而能够同时参与向上、向下的电网频率调节,但该控制器不考虑PV 中的备用功率,可能导致频率调节不均匀。 文献[9]用减载PV 取代了蓄能电池,并对其成本效益进行了优化研究。目前,以惯性响应控制和加储能的方式参与风力发电机系统调频策略已有相关研究[10]~[12],但还未将相关技术应用在PV 系统领域内。 本文提出了一种基于等比例减载控制光伏调频的策略,能够有效地调节PV 系统的频率。 该方法将减载控制器和备用功率相结合, 提高了减载控制的调频能力,并对其成本进行了分析。基于Power Factory 软件对PV 系统进行建模与仿真,并采用IEEE399-1997 系统验证了本文所提控制策略的有效性。
1 光伏发电机建模
为提高PV 系统额定电流, 须要并联多个电池板;为获得更高的电压,须串联多个单元。 其中输出电流Ipv为
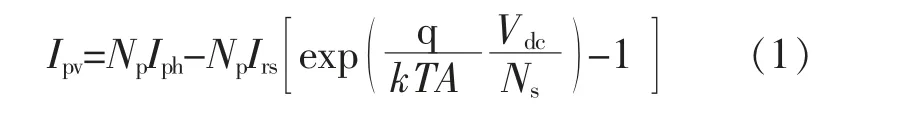
式中:Np为并联单元个数;Ns为串联单元个数;Irs为反向饱和电流;q 为电子电荷,q=1.602×10-19C;k为玻尔兹曼常数,k=1.380 650 3×10-23J/k;A 为理想因子;T 为开尔文温度;Vdc为输出直流电压;Iph为光伏电池的短路电流。
温度T 和光照S 的函数,其表达式为
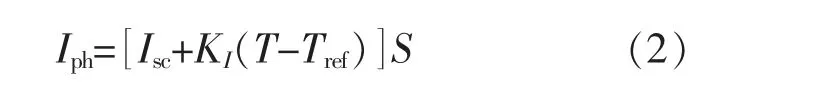
式中:Tref为参考温度;KI为温度系数。
不同环境下MPP 的电压VMPP须要光照强度E 和初始标准电压VMPP0给定,即:
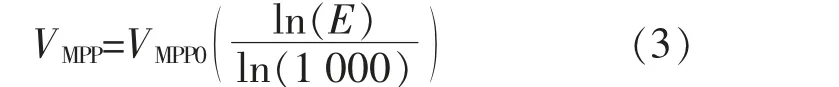
另外, 为了解决PV 发电机受温度影响的问题,模型中引入了校正因子。 采用温度校正系数av

2 光伏发电系统等比例减载运行
2.1 PV 减载控制
通常,PV 系统功率不会随负载而变化, 如果环境条件保持不变,PV 输出固定的有功功率,没有多余的输出功率为电网调节频率, 其原理如图1 所示。
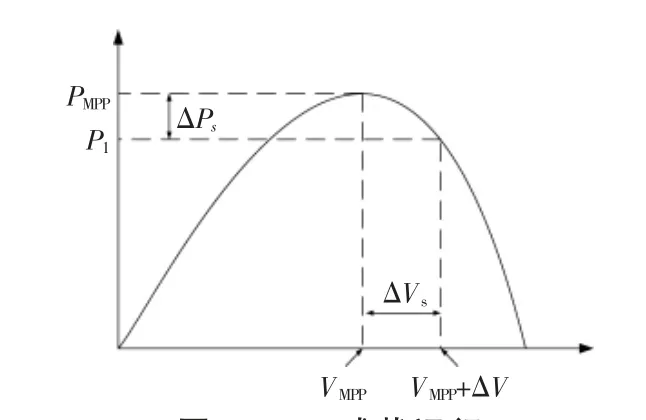
图1 PV 减载运行Fig.1 PV deloading operation
由图1 可知,PV 发电系统为MPP 运行时,直流母线电压为VMPP,输出最大功率为PMPP。 如果运行电压高于VMPP, 则输出功率为P1。 在这种情况下, 因为储备了部分有功功率ΔPs,PV 则处于减载运行状态,其表达式为

本文光伏发电机组控制策略采用分层控制,如图2 所示。分成逆变器控制层、功率控制层和频率控制层三层。
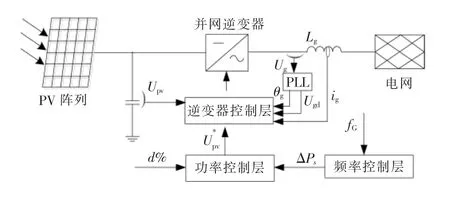
图2 光伏发电分层控制策略Fig.2 Structure block diagram of the proposed controlstrategy
频率响应模块根据电网频率改变光伏阵列的功率输出, 使光伏发电系统能够产生与传统发电机组类似的调频响应,其控制框图如图3 所示。

图3 频率响应控制框图Fig.3 Structure block diagram of frequency response control
图中:f0为额定电网频率;kd为下垂系数;(d%)0为初始减载率;(d%)ref为减载率参考值,作为下一层控制的参考输入。 减载率d%为
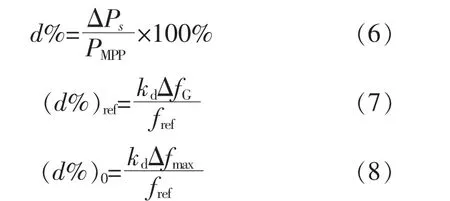
减载控制模块的核心功能是将频率响应的输出(d%)ref转换为光伏阵列直流电压参考值vdcref,本文采用离线数据拟合和在线功率跟踪相结合的方法,其流程如图4 所示。
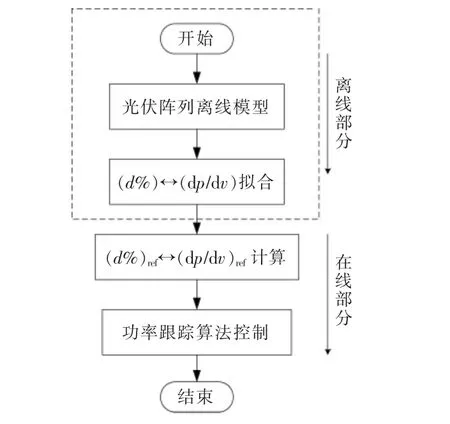
图4 减载控制流程图Fig.4 Flowchart of de-load control
离线部分主要对光伏阵列模型的数据进行分析,进而获得(d%)↔(dp/dv)的关系式为
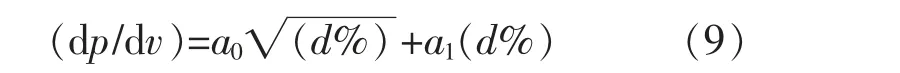
式中:a0,a1为拟合系数[7]。
在线部分通过频率响应模块输出(d%)ref,代入式(9)后获得与(d%)ref对应的(dp/dv)ref。 通过功率跟踪算法, 在线跟踪 (dp/dv)ref所对应的vdcref。最终实现PV 发电系统随频率的变化而减载运行。
2.2 等比例减载模型
若不考虑PV 发电系统的备用功率, 当频率扰动时,不同备用容量的PV 发电系统出力相同,因此, 较少备用的PV 发电系统将无法对系统频率的再次扰动而出力, 这将导致频率调节的分布不均衡。 为使同一机组的所有PV 发电机相互协调,防止部分PV 机组过度调节,本文提出了一种考虑备用功率的等比例控制方法, 使各PV 机组的有功功率分配更加合理。
①根据频率偏差计算光伏电站的有功功率输出值,即:

式中:Pref为光伏电站有功功率的参考值;Pmeas为光伏电站有功功率的测量值;fref为电网系统的参考值;fmeas为电网连接点频率的测量值;kl为光伏发电厂的频率-有功调节系数。
第i 个PV 模块的可调容量占比Pi为

式中:Pmaxi为第i 个PV 模块的最大输出;Pmini为第i 个PV 模块的最小输出;Pbi为第i 个PV 模块的基本输出。
在这种模式下, 每个PV 模块具有相同的可调容量比例Pi,0≤Pi≤1。
②根据可调节容量等比例的模式, 假设光伏电站中有N 个独立的PV 模块, 光伏模块的可调容量比例应满足:

假设光伏电站在扰动发生前的总有功输出为Pzs,第i 个PV 模块的有功输出为Pzi,光伏模块的最大有功输出之和为Pmaxs。第i 个PV 模块所承担的功率变化量为ΔPi,ΔPi为由协调控制系统给出的功率调节命令。 假设光伏电站的总功率变化为Ps,可得到约束条件为

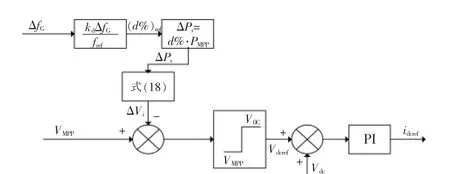
图5 考虑备用等比例减载控制框图Fig.5 Deloading controller considering standbyproportional control
2.3 算例分析
基于Power Factory 平台并采用IEEE399-1997 系统进行仿真,如图6 所示。 系统主要包括2台同步发电机、29 台电动机和12 个PV 发电机组, 其中每个PV 发电机组额定容量为448.5 kW,并分别连接在18,35,37 和49 母线上。
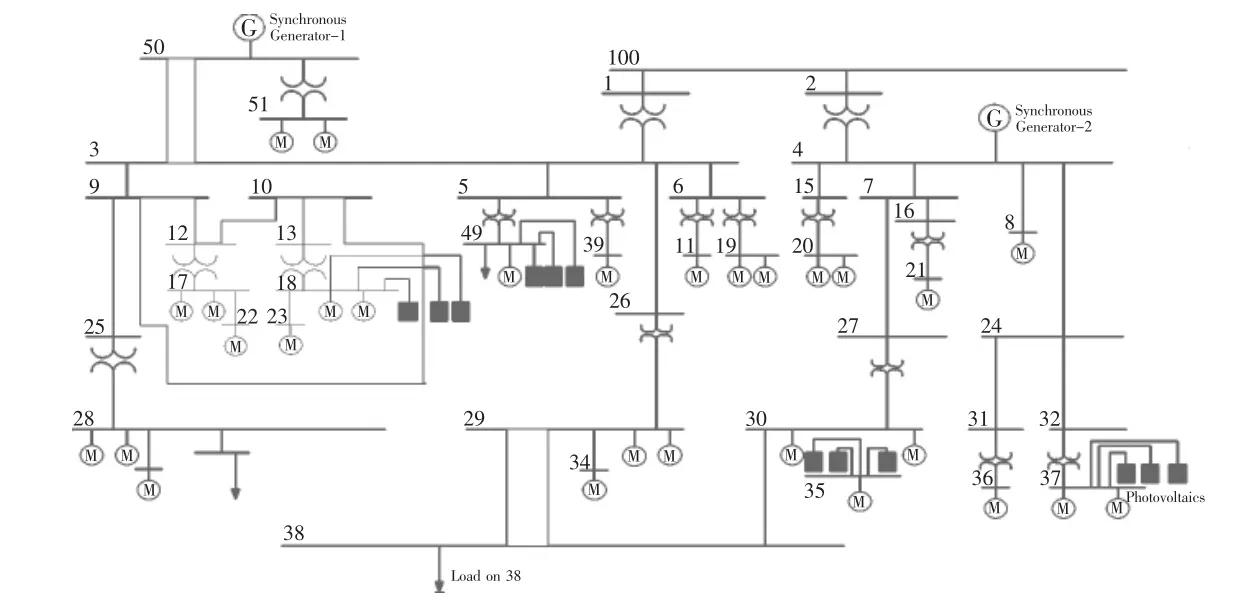
图6 IEEE 399-1997 系统Fig.6 IEEE 399-1997 system
2.3.1 控制参数对PV 功率的影响
仿真中, 每个PV 发电机组均减载18%,而12 个PV 发电机减载后的总备用则为0.972 MW(81 kW×12)[14]。不考虑备用的减载控制器,在50 s时增加负载,并观察PI 控制器的比例增益(KP)和积分增益(Ki)对PV 发电机组及常规发电机输出的影响,如图7,8 所示。
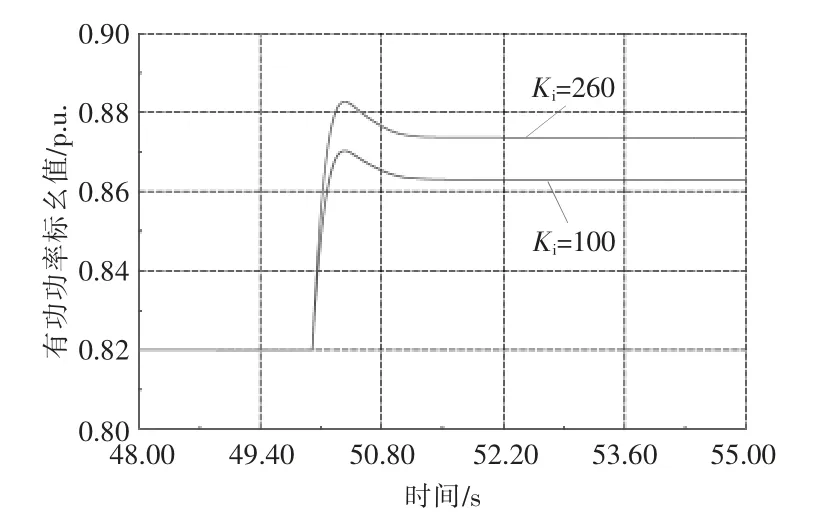
图7 PV 发电机组的有功功率Fig.7 Active power of PV generators
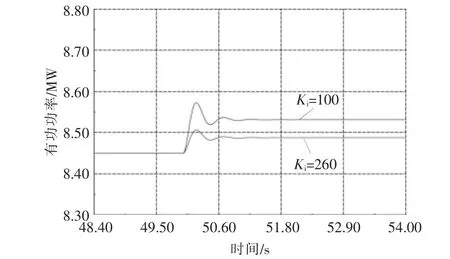
图8 发电机1 的有功功率Fig.8 Active power of generator 1
由于KP对系统输出变化的影响较小,本文仅考虑Ki的影响。 由图7,8 可知,Ki从100 增至260[15],PV 发电机组输出的功率随之增加,而常规发电机的输出功率增量相应减少。 为了调节系统频率,PV 发电机组和常规发电机增加功率输出,其变化情况如图9 所示。
由图9 可知,Ki=260 比Ki=100 时的频率变化曲线波动较小, 且恢复标准频率的时间更快。 因此, 本文所设计的PV 减载控制器对其有功输出和系统频率调节都有较好的效果。
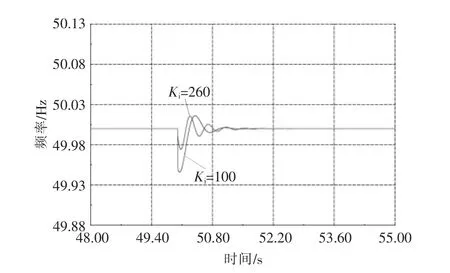
图9 37 母线的频率Fig.9 Frequency of bus 37
2.3.2 两种控制方法的性能比较
在系统频率调整的过程中,当仅考虑频率偏差控制器的作用时,基于减载率为8%,18%情况下的PV 发电机组有功出力如图10 所示。 考虑了有功备用时,PV 发电机组有功出力如图11 所示。
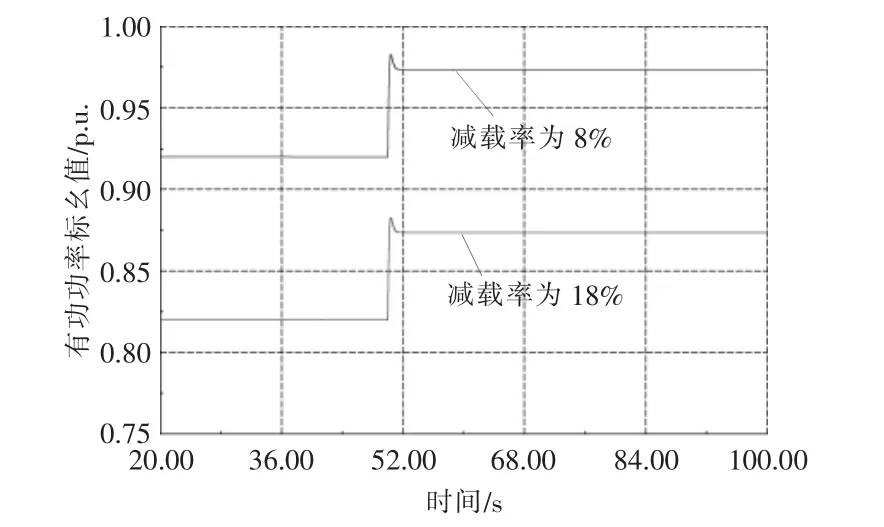
图10 考虑频率偏差PV 有功功率Fig.10 Consider frequency deviation PV active power
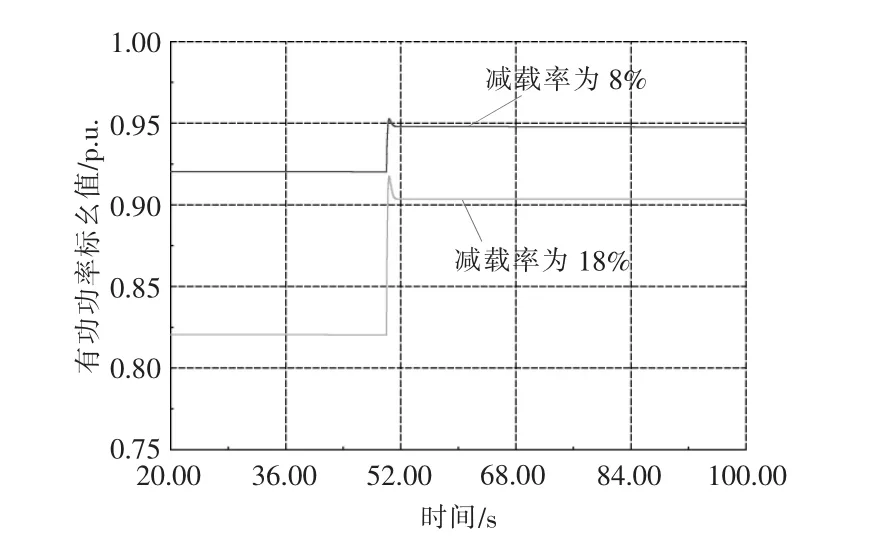
图11 考虑有功备用PV 有功功率Fig.11 Consider active standby PV active power
由图10,11 可知,在控制器运行过程中(不考虑备用功率),面对相同负载的变化,基于两种不同减载率的PV 发电系统输出功率的增量相等。在改进控制器运行过程中(考虑备用功率),面对相同负载的变化, 基于两种不同减载率的PV 发电系统输出功率的增量不等, 且增量按照功率的备用量进行等比例变化。因此,在实际的系统调频过程中, 频率调节控制系统将考虑各PV 机组的实时运行情况, 并按可调容量进行等比例分配有功功率,进而提高了频率控制的精度,有效地避免了PV 发电系统的重复调整运行。
2.4 不同工况下的仿真结果
2.4.1 方案1 仅PV 系统参与频率调节
由于光伏储备足以调节频率,在高光照和小负荷变化的情况下,常规发电机不需要增加出力,PV 发电机组与常规发电机的出力情况如图12,13 所示。
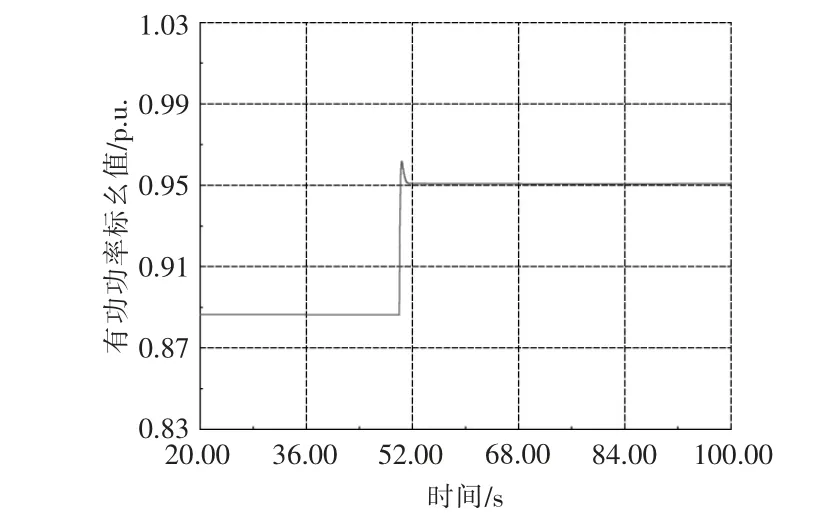
图12 PV 发电机组的有功功率Fig.12 Active power of PV generators
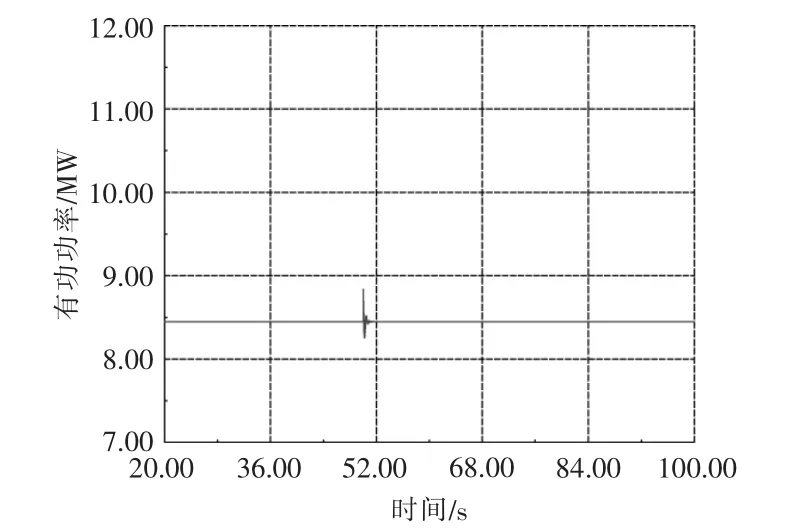
图13 常规发电机的有功功率Fig.13 Active power of the conventional generator
2.4.2 方案2 PV 系统备用耗尽, 常规发电机参与频率调节
在高负荷变化的情况下, 即使PV 发电机光照强度与方案1 相同,PV 发电机也将达到MPP,在此情况下,其有功功率出力如图14 所示,而常规发电机增加出力以达到平衡负荷的要求, 其具体情况如图15 所示。
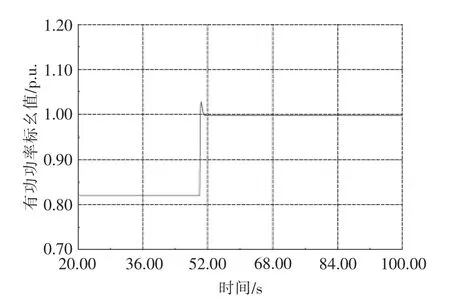
图14 PV 发电机组的有功功率Fig.14 Active power of PV generators
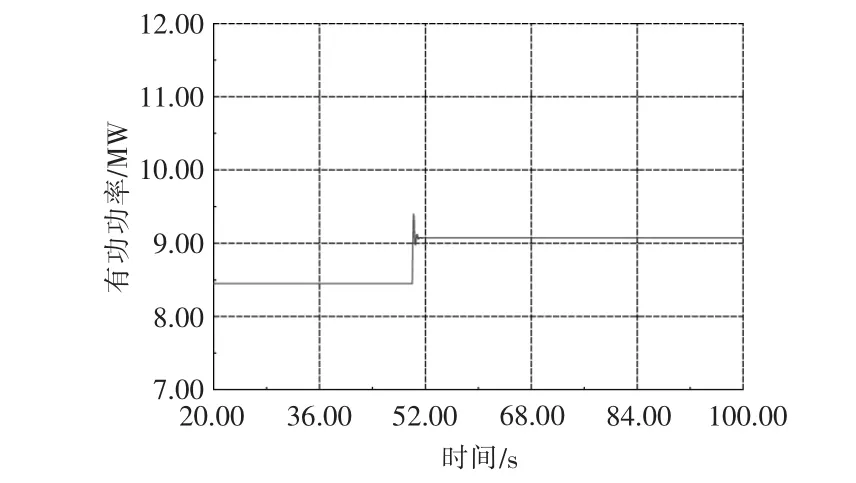
图15 常规发电机的有功功率Fig.15 Active power of the conventional generator
3 成本分析
PV 减载将导致其利用率下降,而经济成本与加电池储能调频相比显得尤为重要。 两种频率调节方案的成本差异在于, 一是需要增加PV 的面板尺寸,二是需要额外的储能电池。 因此,本文将对增加的面板尺寸所需成本与加储能电池的成本进行比较。
在模拟系统中,提供的备用容量接近1 MW。其造价成本将被视为额外支出。 根据近两年的光伏产业行情,1 MW 的总费用约为525 万元。
如果PV 在MPP 工况下增加储能电池,则电池的成本取决于电池容量大小。 如果减载光伏的频率调节储备为1 MW, 则其成本将与1 MW 大小的电池进行比较。 由于每个地理位置的光照强度不同, 因此PV 发电机可能会提供较低的输出功率。 对于这样的系统,对增加PV 面板的成本与容量较小的电池进行对比则更为合理。例如,如果只有0.5 MW 备用可用于频率调节, 则须要将其成本与仅为0.5 MW 的电池进行比较。 因此,本文以不同的蓄电池容量作为备用, 对1 MW 及以外的PV 发电容量进行了成本效益分析。 表1 计算了每2 a 更换一次铅酸电池的电池成本, 并假设标准光照强度下的PV 面板的预期寿命约为24 a。 其中材料成本a、运营成本b 和回收价值c 分别为
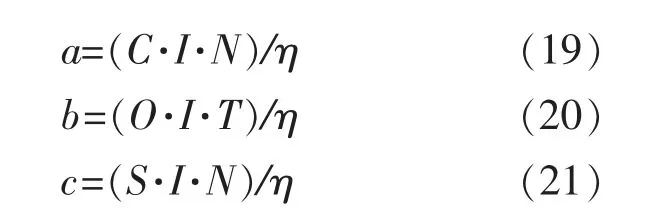
式中:C 为单位材料成本,C=1 540 元/kW;I 为单位装机容量;N 为电池更换的次数;O 为单位运行成 本,O=140 元/kW;S 为 单 位 回 收 成 本,S=14元/kW;T 为使用寿命;η 为电池效率,取0.85。
由表1 可知: 由1 MW 面板提供的备用成本比1 MW 储能电池节省2 025 万元。 随着电池容量的减小,电池的效益也随之降低,进而节省费用的多少取决于所选择的电池容量; 当光照稳定在标准强度时,系统增加1 MW PV 面板的成本相当于0.205 91 MW 电池的成本, 因而PV 备用成本与储能电池成本均处于盈亏平衡点。
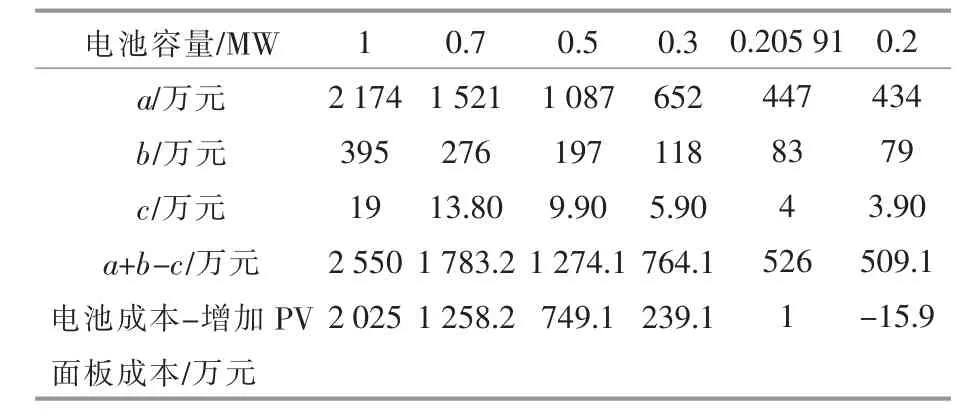
表1 不同容量电池的成本Table 1 Cost of batteries with different capacities
与蓄电池备用相比,PV 发电机组为频率调节提供备用功率是较合理的解决方案,在此基础上,就光照水平较强的地区而言, 通过PV 减载调节系统频率是一种更加经济的选择。
4 结束语
为使PV 系统能主动参与电力系统频率的调节,本文提出了一种基于等比例减载的控制策略,该方法在传统的减载控制基础上, 考虑了备用功率对光伏输出的影响, 使不同备用容量的PV 参与频率调节,进而对减载控制器进行优化,最终使系统频率稳定。 在Power Factory 环境下对IEEE399-1997 系统进行仿真,验证了本文所提方法优于考虑储能的频率控制方法。
