3段式集成DFB激光器微波信号仿真
2020-09-16乔丽君张明江张建忠
孟 洁,乔丽君,张明江,张建忠,王 涛
1)太原理工大学新型传感器与智能控制教育部与山西省重点实验室,山西太原 030024;2)太原理工大学物理与光电工程学院,光电工程研究所,山西太原 030024
微波因具有似光性、穿透性及非电离性等特点,主要应用于雷达、卫星传输及移动通信等领域.在光域中产生的微波信号具有操作带宽大、高频、功耗低及抗电磁干扰等优势[1-6],受到广泛研究关注.产生微波信号的光学方法包括光学外差法[7]、光注入锁相法[8]、光学倍频法[9]、光学非线性法[10]及外调制法[11]等.沈颖等[12]利用环形腔结构产生多级布里渊散射信号,并利用马赫-曾德尔调制器产生4阶边带信号,通过将多级布里渊散射信号对4阶边带信号进行放大后与载波信号拍频,得到高频微波信号,该方法倍频效率高,但微波信号生成系统较复杂;熊锦添等[13]利用分布反馈(distributed feedback, DFB)激光器放大探测光2级边带,产生基于二倍频本地振荡信号的微波信号;RASHIDINEJAD等[14]基于光电振荡器与相位调制器构成的环形腔结构产生微波信号,但该方法的可调频带仅为500 MHz;张鹏等[15]提出一种8字型结构光纤激光器,利用布里渊多波长光纤激光器产生高频微波信号,但该结构中光纤长度较长,容易增加微波信号线宽;李玲等[16]基于双波长激光器件,利用非线性偏振旋转产生光学微波信号;JAIN等[17]利用外调制法改变强度调制器的调制深度产生微波信号,但该方法插入损耗较大、系统较复杂;梁卿等[18]基于垂直腔面发射激光器,在平行偏振光注入条件下引入光电负反馈,得到微波信号;庞海越等[19]基于光注入半导体激光器,引入光电环路结构,优化微波信号的性能,得到可调谐微波信号;尚海燕等[20]则基于光学外差法利用掺铒光纤激光器,使3束波长不同的光信号拍频得到微波信号,该方法易出现信号功率被抑制的现象.上述方法皆基于分立式器件搭建而成,易受环境影响,性能不稳定,限制了微波信号的应用范围.
本研究基于光注入方法,利用麦克斯韦方程,结合DFB激光器载流子变化规律,建立3段式单片集成DFB激光器的行波速率方程模型并搭建仿真结构,成功生成微波信号,通过研究集成激光器中各段结构偏置电流及光波导失谐量对微波信号的影响,对微波信号时序、光谱和频谱等特性进行模拟分析,结果发现信号频谱随着右侧DFB激光器偏置电流的增加进入强注入锁定状态,最终不再存在拍频分量;由于右侧DFB激光器的注入锁定现象,波导偏置电流对微波生成影响较小;对波导失谐量进行调节,可对微波信号实现14.29 GHz的调谐范围.
1 器件仿真结构
单片集成半导体激光器芯片具有尺寸小、成本低及稳定性好等特点,适用于大批量生产.DFB激光器内置了布拉格光栅,其单色性好、线宽窄、边模抑制比高.因此,本研究从单片集成层面设计3段式DFB激光器芯片结构,仿真分析微波信号的产生及特性.
图1为基于单片集成的3段式DFB激光器芯片结构,沿光轴方向由左至右依次为半导体激光器DFB1、无源光波导WG(waveguide)、半导体激光器DFB2,3段结构之间电学隔离理想.仿真中DFB激光器利用布拉格光栅进行模式选择,由于单片集成结构两端面(DFB1左端面与DFB2右端面)采用理想无损耗端面,且激光器与波导耦合端面(DFB1右端面、WG两端端面与DFB2左端面)无损耗传输光,则6个端面的反射率均为0.设定单片集成3段式DFB激光器总长为 1 050 μm,其中,两段DFB半导体激光器长度与WG长度均为350 μm.

图1 3段式单片集成DFB激光器器件结构示意图
2 仿真原理及模型
单片集成DFB激光器的腔长较短,俄歇效应不可忽略,同时考虑DFB激光器腔内载流子密度等参数的影响,本研究基于行波速率方程对多段式单片集成DFB激光器进行数值模拟,分析其相关动态特性.
行波速率方程的基本数学模型是麦克斯韦-布洛赫方程,从光场、载流子密度和极化函数方面进行数值分析.由于仿真模拟的量变化相对缓慢,因此,忽略快速振动因素所产生的影响,添加外部泵浦激光项和阻尼振荡因素项,从而得到缓变包络近似下的麦克斯韦-布洛赫方程为
(1)
(2)
(3)
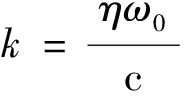
依据上述麦克斯韦-布洛赫方程,结合DFB激光器中载流子的变化规律,推导出缓变包络近似条件下的行波速率方程组为
(4)
(5)

Un=An+Bn2+Cn3
(6)
其中,A为非辐射复合系数,表示由非辐射俘获(反射和吸收)所引起的内部光损耗;B为双原子辐射复合系数;C为俄歇复合系数.
3 实验结果分析
利用行波速率方程对上述3段式单片集成DFB激光器输出信号的时序、光谱及频谱特性进行数值模拟.模拟中DFB激光器的参数值如表1.

表1 仿真模拟的DFB激光器参数值
3.1 DFB2激光器偏置电流对微波信号产生的影响
3段式单片集成器件中DFB1和DFB2激光器区布拉格光栅参数相同,当DFB2和DFB1之间的失谐量为5 GHz时,DFB1激光器偏置电流设为1.5Ith(Ith为阈值电流),将DFB2激光器的偏置电流分别设置为2Ith、4Ith及6Ith,同时波导区偏置电流值设为0,分析集成激光器的时序、光谱及频谱特性,结果如图2.
由图2可见,当DFB2激光器的偏置电流为2Ith时,互耦合激光器出现频率锁定,光谱中有2个主要模式激射,频率分别为458 GHz和462 GHz,频谱中能量最高的频率分量为2个模式的差频(4.105 GHz).时序为周期0.24 ns的脉冲输出,与差频频率对应;当DFB2激光器偏置电流为4Ith时,由拍频导致的频率分量减少;当DFB2激光器偏置电流为6Ith时,形成强注入锁定状态,其频谱中不再存在拍频分量.
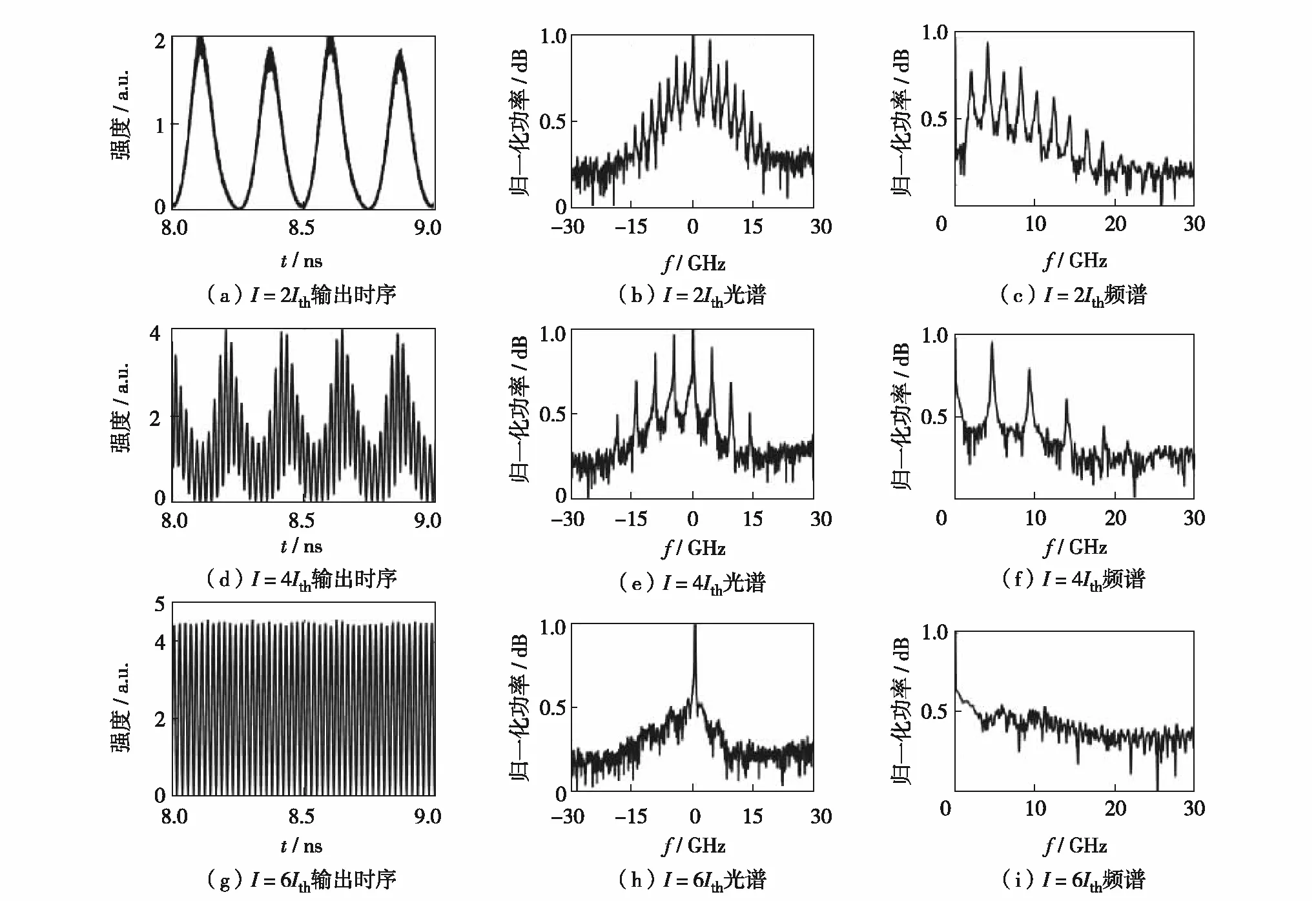
图2 不同DFB2激光器偏置电流下的集成激光器时序、光谱及频谱特性
3.2 波导区偏置电流对微波信号产生的影响
将3段式单片集成DFB激光器中的两段激光器内部布拉格光栅设置为周期相同的光栅,DFB2和DFB1激光器之间的带隙失谐量设为800 GHz,DFB1激光器偏置电流设为1.5Ith,DFB2激光器偏置电流设为5Ith.WG段的失谐量为0,将WG段偏置电流分别设置为2Ith、3Ith、4Ith及5Ith时,集成激光器的时序、光谱及频谱特性如图3.
由图3可见,当波导区偏置电流为2Ith时,得到频率为11.76 GHz的微波信号,与光谱中主模式之间差频相吻合.DFB2和DFB1激光器间的失谐量与所得到的差频不同,认为是集成激光器腔模式与光栅共同作用的结果.逐渐增大波导的偏置电流,集成激光器输出微波的频率基本保持不变,表明在波导区无失谐时,其偏置电流对微波产生的影响很小,由DFB2激光器的注入锁定所引起.
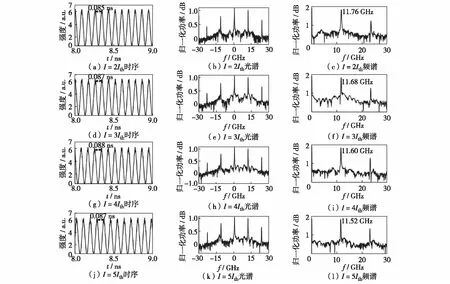
图3 不同WG偏置电流下的集成激光器时序、光谱及频谱特性
3.3 WG带隙失谐量对微波信号产生的影响
将3段式单片集成DFB激光器中的两段激光器内部布拉格光栅设置为周期相同的光栅,DFB1和DFB2激光器的带隙失谐量分别为0和800 GHz,DFB1激光器偏置电流设为1.5Ith,DFB2激光器偏置电流设为5Ith,WG段偏置电流设为4Ith.当WG段带隙失谐量分别设为0、5及24 THz时,集成激光器的时序、光谱及频谱特性如图4.

图4 WG段不同带隙失谐量下的集成激光器时序、光谱及频谱特性
由图4可见,当波导区失谐量为0时,类似于之前的分析,研究得到11.60 GHz的微波信号;当波导区的失谐量为5 THz时,其对集成激光器的光场有较强的调制作用,DFB1激光器的主模式被抑制,相应得到25.02 GHz的微波信号;当波导区的失谐量增大到24 THz时,波导区对光场基本没有调制作用,频谱中除了2个主模式差频25.89 GHz的频率分量,还可以看到激光器的弛豫振荡频率为4.5 GHz.因此,不同失谐量的波导区对该集成激光器的光场具有不同的调谐,通过调节失谐量,可以实现14.29 GHz的调谐范围,这一结果为实验研究提供必要的理论指导.
结 语
设计面向微波信号生成的3段式单片集成DFB半导体激光器,并对生成的微波信号特性进行研究分析.基于光注入法,设计由激光器DFB1、WG及DFB2依次排布的3段式单片集成激光器仿真结构,以此结构结合DFB激光器中载流子变化规律,在麦克斯韦-布洛赫方程的数学模型基础上,确定集成激光器的行波速率方程组.利用该方程组仿真3段式单片集成DFB激光器,对其生成微波信号的时序、光谱及频谱进行数值分析.结果表明,微波信号的时序周期与频谱差频频率对应,当DFB2的偏置电流增大到6Ith时,集成激光器形成强注入锁定状态,频谱中不再存在拍频分量;在激光器形成注入锁定后,微波频率随WG偏置电流的增大基本保持不变;通过调节波导失谐量最终可实现对微波信号14.29 GHz的调谐范围.所取得结论为集成器件生成可调谐微波信号提供了理论支持.
