叶片脱落诱发的转子-盘片系统不平衡响应分析
2020-09-16陈雪莲范晓宇
陈雪莲,曾 劲,马 辉,4,范晓宇
(1.辽宁省交通高等专科学校信息工程系,沈阳110122;2.中国科学院沈阳自动化研究所,沈阳110014;3.东北大学机械工程与自动化学院,沈阳110819;4 东北大学航空动力装备振动及控制教育部重点实验室,沈阳110819;5 中国航发沈阳黎明航空发动机有限责任公司,沈阳110043)
0 引言
航空发动机通常运行在高速、高温等恶劣工作环境中,在复杂的周期性交变载荷作用下,譬如气动力、碰摩力等,极易导致叶片因发生疲劳失效而产生飞失现象[1-3]。叶片飞失是航空发动机遭遇的1 种典型恶劣载荷工况,为此,美国联邦航空管理局、欧洲航空安全局和中国民航局均对航空发动机中叶片丢失工况下的安全性设计提出了要求[4-6]。
很多学者以叶片飞失事件为背景开展了大量研究工作。Shmotin 等[7]和Cosme 等[8]进行了机匣的包容性研究,其主要关注断叶-机匣间的短时冲击响应;Ortiz 等[9]基于显式有限元分析软件Europlexus 分析了低压涡轮叶片在部分和整体飞失条件下对涡轴发动机系统动响应的影响;Carney 等[10]和Jain 等[11]基于LS-DYNA 分析软件模拟了断叶-机匣/断叶-动叶间的相互作用过程;Heidari 等[12]基于MD Nastran 分析软件,采用隐式-显式-隐式的分析流程讨论叶片飞脱导致的碰摩动力学特性;He 等[13-15]基于LS-DYNA分析软件开展了某型航空发动机断叶-机匣的包容性仿真工作,并进行了试验验证;Sarkar 等[16]基于Dyna3d 显示有限元分析软件对T58 转子分别进行了单叶片和3 叶片飞失下的机匣包容性仿真和试验。
以上研究多借助显示有限元分析软件开展断叶飞失条件下的机匣包容性研究,更多关注的是断叶-机匣间的瞬态冲击过程,较少涉及讨论叶片丢失事件对失衡转子动力学特性的影响规律。基于此,本文主要借助ANSYS 和LS-DYNA 2 款分析软件,建立了弹性支承下转子-盘片系统的有限元模型,同时考虑叶片飞失效应的影响,进一步研究了转子转速、不平衡量、盘偏置量和弹性支承刚度等参数对失衡转子系统动力学特性的影响规律。
1 显式动力学有限元法基本理论
转子-盘片系统单元离散化后的动力学方程为
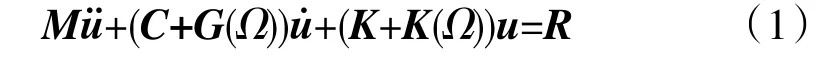
式中:M、C 和K 分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;K(Ω)为由于旋转效应导致的附加刚度矩阵;G(Ω)为与转速相关的陀螺矩阵;和u 分别为系统加速度向量、速度向量和位移向量;R 为外载荷向量。
系统阻尼矩阵C 采用瑞利阻尼进行计算

式中:α 和β 为瑞利阻尼系数,本文研究中定义频带在[30,600] Hz 内的阻尼比为0.01,依此确定α 和β。
对式(1)采用中心差分法进行求解[17]。
2 转子- 盘片- 弹簧阻尼支承系统的有限元模型
出于计算分析的需要,本文对系统进行如下简化:
(1)实际轴承支承结构过于复杂,本文采用弹簧阻尼单元近似模拟;
(2)在分析过程中忽略重力对系统振动响应的影响;
(3)忽略扭形叶片和轮盘、轮盘和转轴之间的接触关系,采用共节点方式连接;
(4)忽略叶片飞失过程中裂纹的扩展过程,断叶被假定是瞬断的;
(5)忽略负载的影响。
转子-盘片-弹簧阻尼支承系统的有限元模型如图1(a)所示,缺陷叶片如图1(b)所示,转轴的具体尺寸参数以及轮盘偏置量d 如图1(c)所示。需要指出的是,本文将距左、右端面各5 mm 的区域(图1(c)中紫色区域)设置为刚性体,仅保留刚性体沿x 轴和y 轴的平动自由度和绕z 轴的转动自由度。驱动转速n 施加于刚性体上,以驱动系统运转。
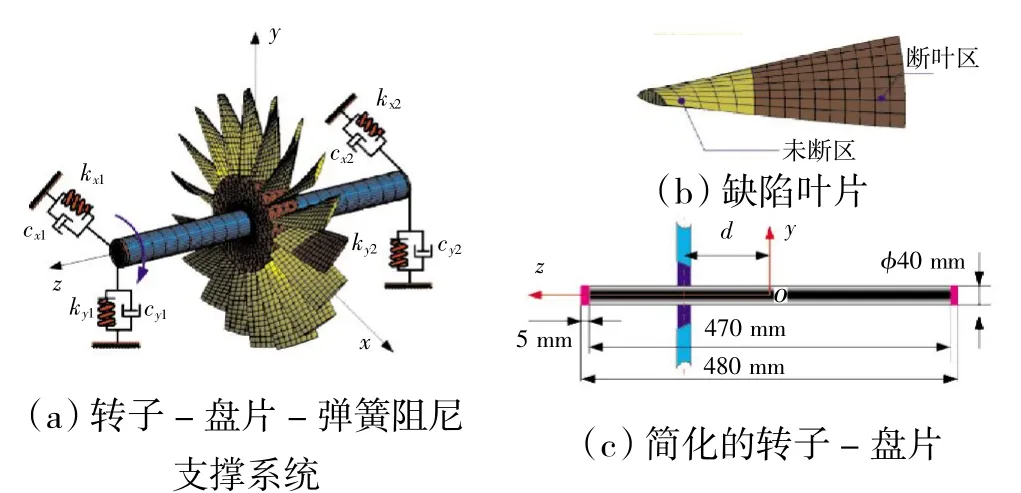
图1 转子-盘片-弹簧阻尼支承系统
系统相关材料参数设置见表1。叶片选用双线性随动强化材料模型(Bilinear Kinematic Model,BKIN),且忽略动态应变率效应的影响,而转轴和轮盘则采用各向同性的线弹性材料模型(Isotropic Elastic Model)。此外,叶片飞失模拟通过对断叶区指定一特定的飞失时刻tf,当求解时间t≥tf,处于断叶区内的单元自动被删除,从而模拟叶片飞失。
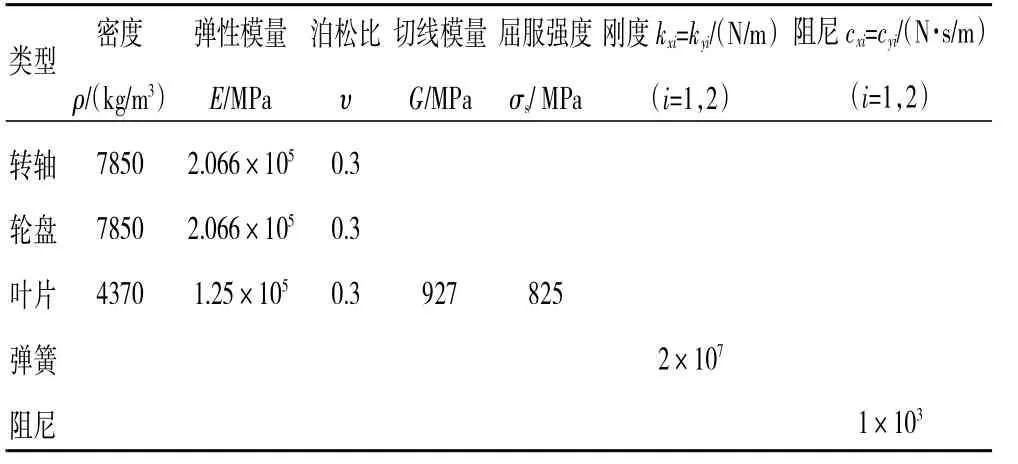
表1 转子-盘片-弹簧阻尼支承系统参数
3 叶片丢失激励下系统的振动响应分析
本章分析转子-盘片-弹簧阻尼支承系统在叶片飞失情况下的动力学响应,重点分析转速n、不平衡量e(缺陷叶片中考虑断叶区飞失引入的不平衡量,图1(b))、盘偏置量d和轴承支撑刚度kxi、kyi(i=1,2)对系统振动响应的影响。此外,为了考虑转速这一预载荷对系统振动响应的影响[18],本文采用隐式- 显式序列进行系统振动响应的求解,其分析流程如图2 所示。
数据提取包括盘心在x 和y 方向的振动位移(x(t)、y(t))以及左端和右端轴承在x 和y 向的弹簧力、阻尼力Fkxi(t)和Fkyi(t)为弹簧力,Fcxi(t)和Fcyi(t)为阻尼力),并根据所提取的数据通过合成进一步得到盘心的径向位移r(t)和轴承支承总反力F(t),相应的计算表达式为

图2 隐-显式分析流程
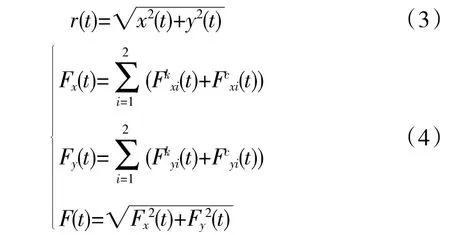
此外,为便于描述,分别定义瞬态无量纲幅值比βmax和稳态无量纲幅值比βmean
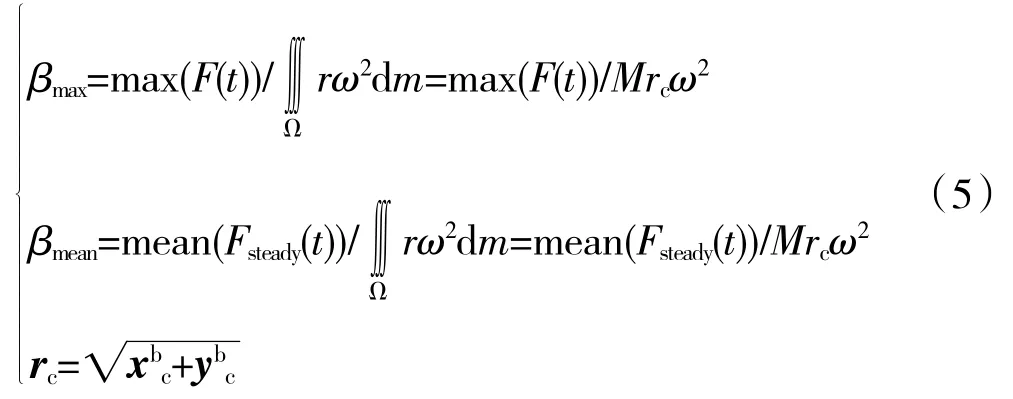
式中:max(·)和mean(·)分别为取最大值和均值函数;(Fsteady(t)为轴承支承总反力的稳态部分时域曲线;M 为单叶片的总质量,M=0.13517 kg;为单个叶片质心距z 轴的距离;ω 为转子转速,ω=πn/30 rad/s;xbc和ybc分别为单个叶片质心在x 和y 方向的坐标,xbc=120.33 mm,ybc=9.08 mm。
3.1 转速对系统振动响应的影响
在工况1 下盘心在x 和y 方向的振动响应以及轴心轨迹(仿真参数见表2)如图3 所示。从图中可见,叶片飞失前盘心的振动幅值较小,轴心轨迹为1个较小的椭圆,这主要是由于系统结构为周期对称结构且受力均衡所致;在叶片飞失瞬间,x 和y 向振动幅值以及轴心轨迹出现明显放大现象,这主要是由于断叶飞失引入的突加不平衡力对系统造成瞬时冲击。在不同转速下的盘心运动轨迹如图4 所示(仿真参数见表2)。从图中可见,在工况4 下的轴心轨迹较其他工况下的明显放大,这主要是由于此转速接近叶片飞失后系统的固有频率而发生的共振现象。

表2 转速n 的仿真参数
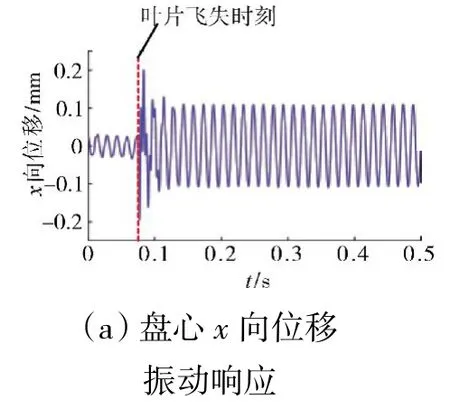
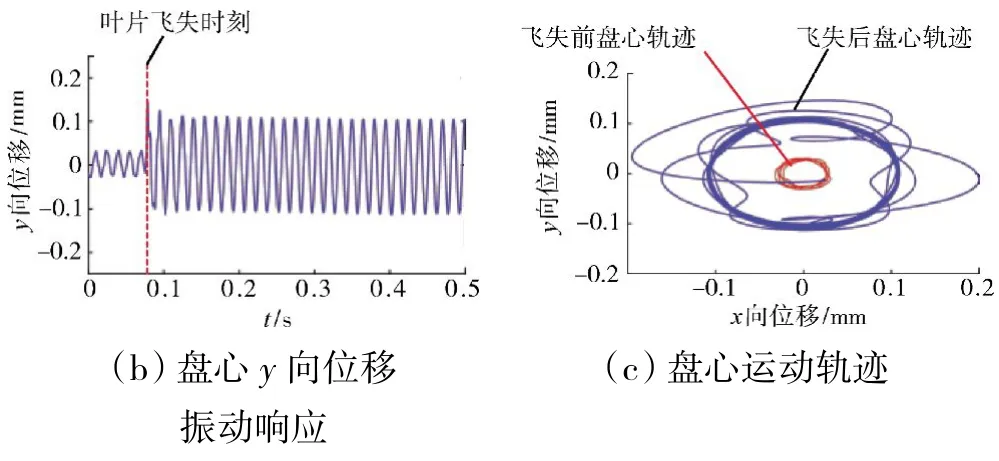
图3 工况1 下盘心振动响应及运动轨迹
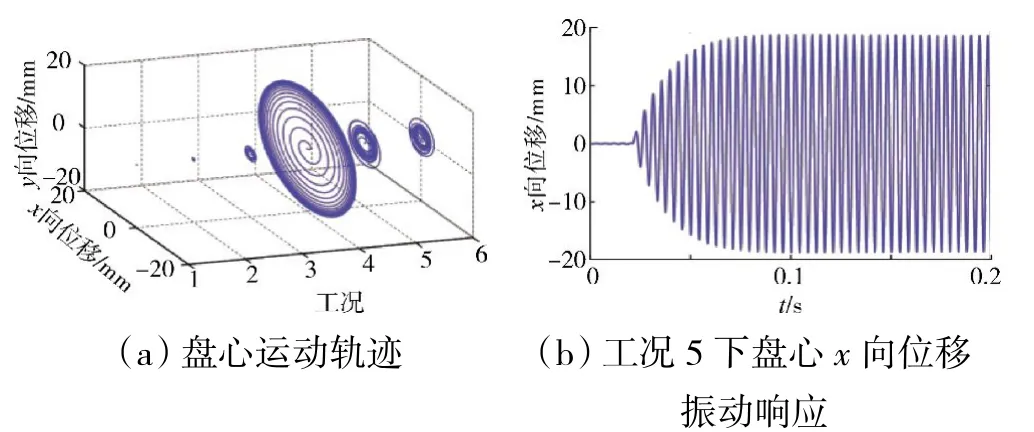
图4 不同转速下的盘心运动轨迹
径向位移rmax和rmean随转速的变化规律如图5(a)所示。从图中可见,径向位移以近共振转速为界,往两边呈现出递减的趋势。其中,rmax为径向位移时程曲线中的最大值,rmean则为稳态响应中的均值(如图5(b)所示)。
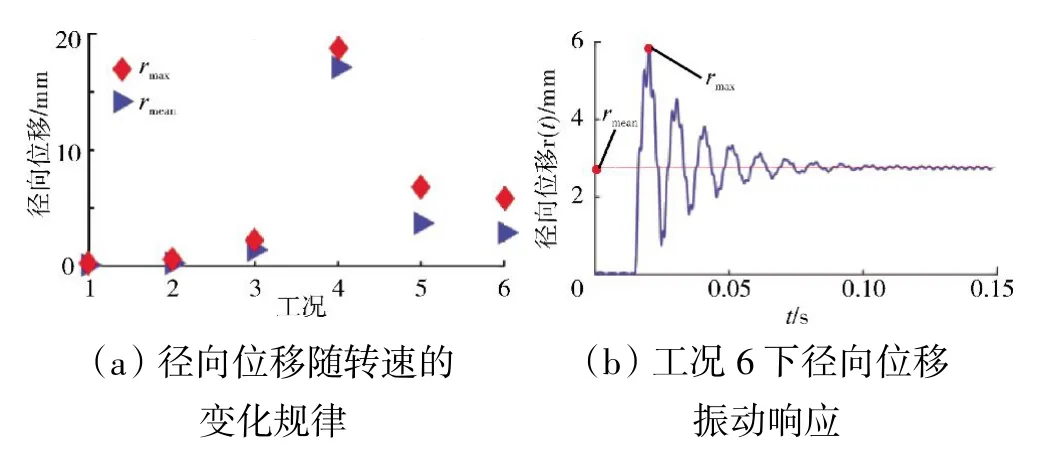
图5 径向位移幅值随转速的变化规律
系统的轴承支承总反力时域曲线和无量纲幅值比变化规律如图6 所示。从图6(a)中可见,断叶飞失会对系统产生1 个瞬时冲击,此外,在近共振转速下轴承支承总反力最大。不平衡力幅值比随转速的变化规律如图6(b)所示。从图中可见,在低转速区,轴承支承总反力和断叶飞失引入的不平衡力(eω2)近似相等;随着转速的升高,轴承支承总反力呈现出先增大后减小的趋势,在近共振处达到最大值。
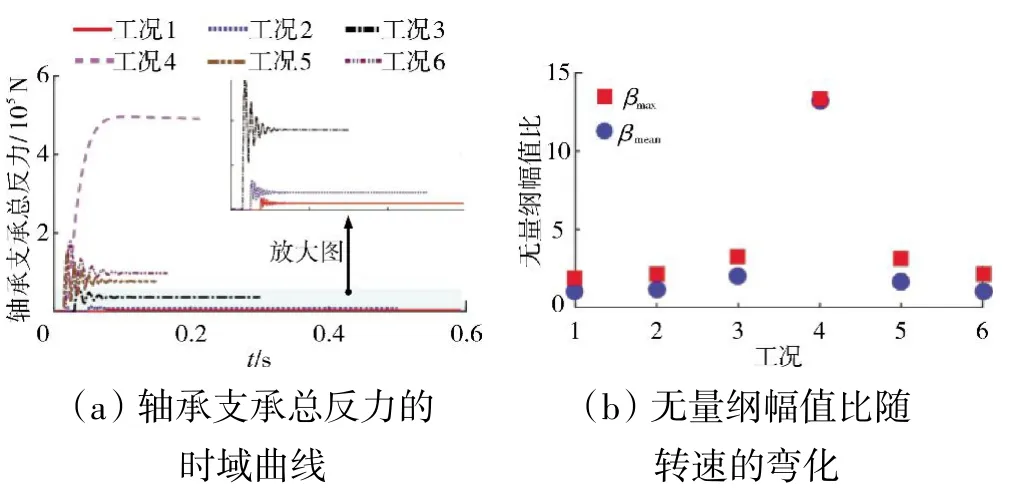
图6 轴承支承总反力时域曲线及无量纲幅值比
在不同转速下,取左端轴承x 方向支承反力的稳态响应部分得到的3 维谱如图7 所示。从图中可见,谱图中只出现了明显的转频成分,且在近共振转速处(工况4)出现了明显的幅值放大现象(系统在14400 r/min 时的1 阶正进动频率约为237.85 Hz)。
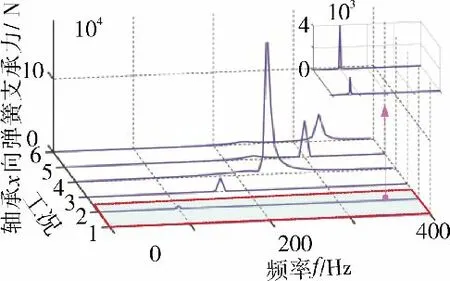
图7 左端轴承x 方向支承反力的3 维谱
3.2 不平衡量对系统振动响应的影响
盘心运动轨迹和径向位移(rmax,rmean)随不平衡量e 的变化规律如图8 所示(仿真参数见表3)。从图中可见,不平衡量e 的增加导致盘心运动轨迹增大以及rmax和rmean间差距更加明显。这主要是由于不平衡量e越大,系统引入的突加不平衡力越大,叶片丢失瞬间对系统冲击振动响应的影响越明显。图9(a)、(b)中轴承支承总反力的变化规律同样证明这一现象。图9(c)、(d)表明轴承支撑总反力的变化主要取决于系统的不平衡量。在不同不平衡量e 下,取左端轴承x方向支承反力的稳态响应所作的3 维谱如图10所示。从图中可见,谱图中仅存在转频成分,且转频幅值与不平衡量e 成正相关关系。

表3 不平衡量e 的仿真参数
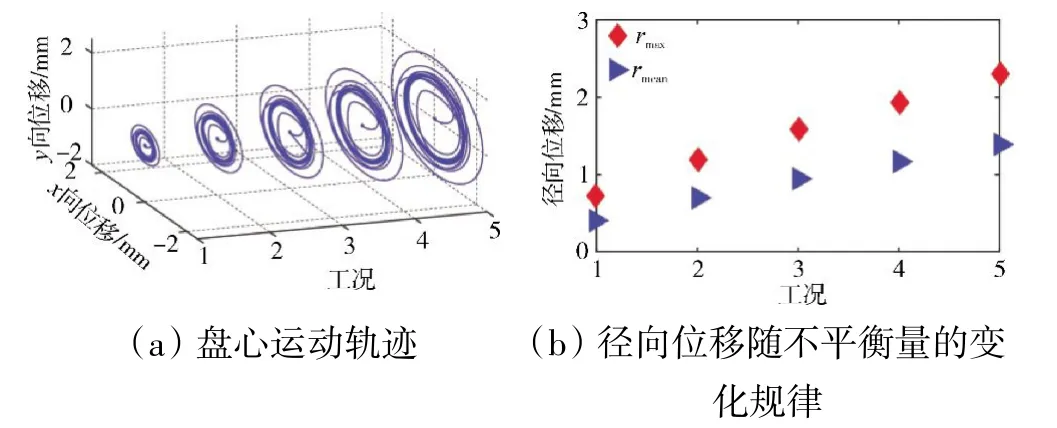
图8 不同不平衡量e 下的盘心运动轨迹及径向位移
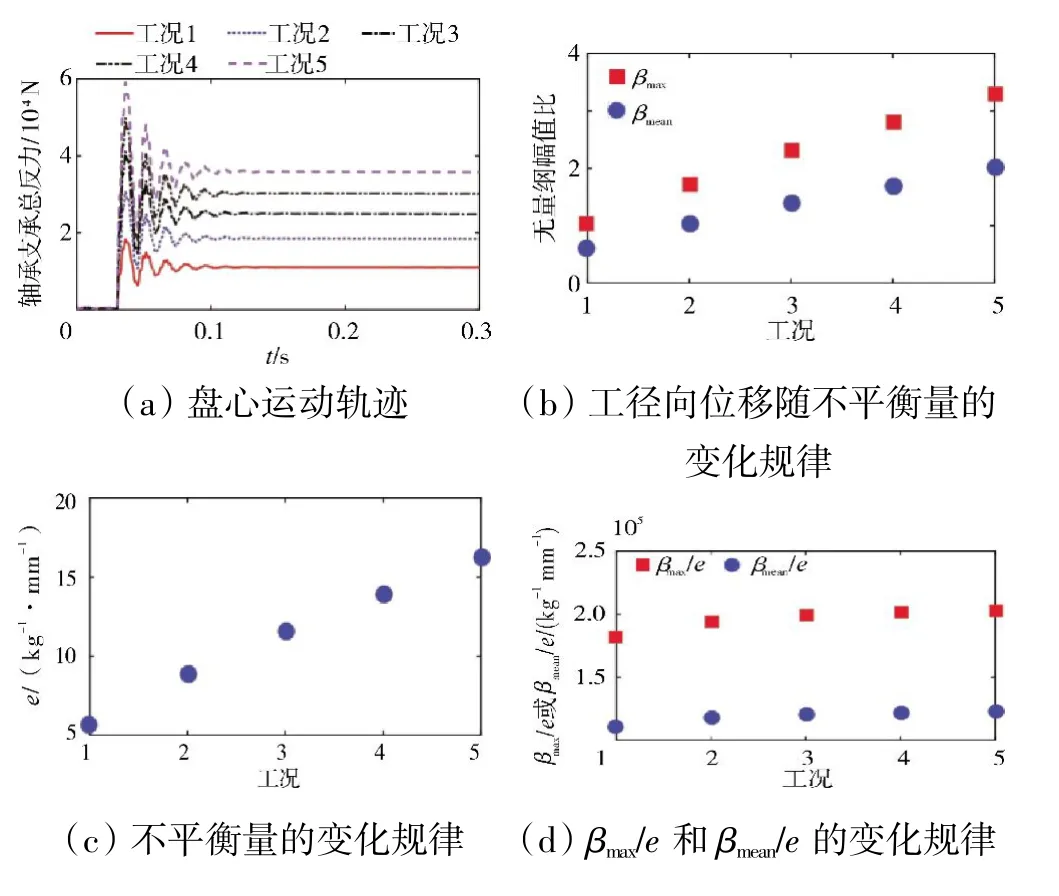
图9 不平衡量e 对系统振动响应的影响
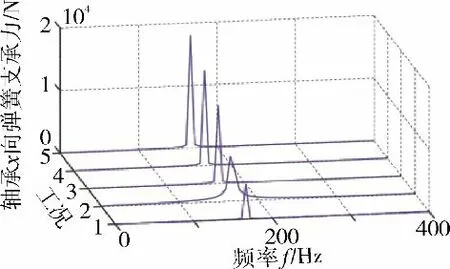
图10 左端轴承x 方向支承反力的3 维谱
3.3 盘偏置量对系统振动响应的影响
不同盘偏置量d 对盘心运动轨迹及径向位移(rmax,rmean)的影响规律(仿真参数见表4)如图11 所示。从图中可见,当d=0 mm 时,所得轴心运动轨迹和径向位移(rmax,rmean)最大。轴承支承总反力以及无量纲幅值比的变化规律如图12 所示。由图中可见,在d=-100 mm 和d=100 mm 时的轴承支承总反力时域曲线和无量纲幅值比几乎相同,而在d=-50 mm 和d=50 mm 时的轴承支承总反力时域曲线和无量纲幅值比存在一些差别。在d=0 mm 时,系统的轴承支承总反力和无量纲幅值比达到最大值。左端轴承x 方向支承反力的3 维谱(如图13 所示)同样反映了这一规律。造成这种现象的原因主要是由于轮盘结构的锥度特征(图1)和盘偏置耦合所致。

表4 盘偏置量d 的仿真参数

图11 不同盘偏置量下的盘心运动轨迹以及径向位移
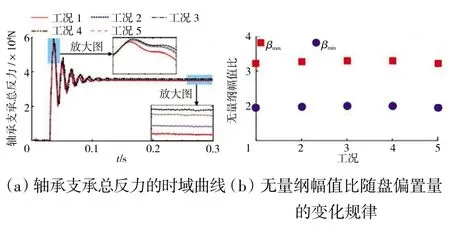
图12 轴承支承总反力的时域曲线以及无量纲幅值比
3.4 支承刚度对系统振动响应的影响
支承刚度对盘心运动轨迹和径向位移(rmax,rmean)的影响规律(相关仿真参数见表5)如图14 所示。图14(a)表明轴承支承刚度对转轴的瞬态涡动轨迹影响最为明显;图14(b)则说明系统的瞬态径向位移rmax与弹簧支承刚度成反相关关系,且在大支承刚度下,瞬态径向位移rmax和稳态径向位移rmean几乎相同。在较大的轴承支承刚度下(工况4),轴承支承总反力的时域曲线波动较为剧烈,如图15 所示。左端轴承处x 方向支承反力在不同支承刚度下的3 维谱如图16 所示。在支承刚度为2×107N/m 下的轴承反力较其他支承刚度下的大。
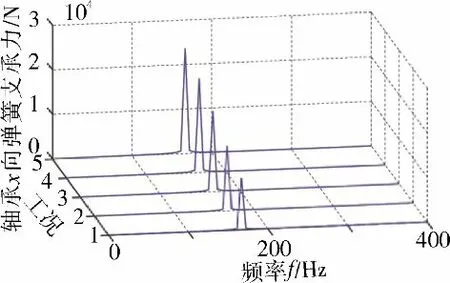
图13 左端轴承x 方向支承反力的3 维谱

表5 支承刚度的仿真参数
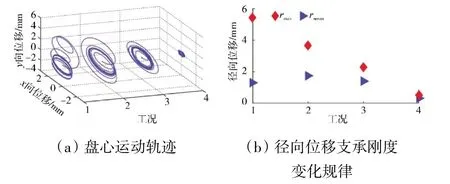
图14 不同支承刚度下的盘心运动轨迹以及径向位移
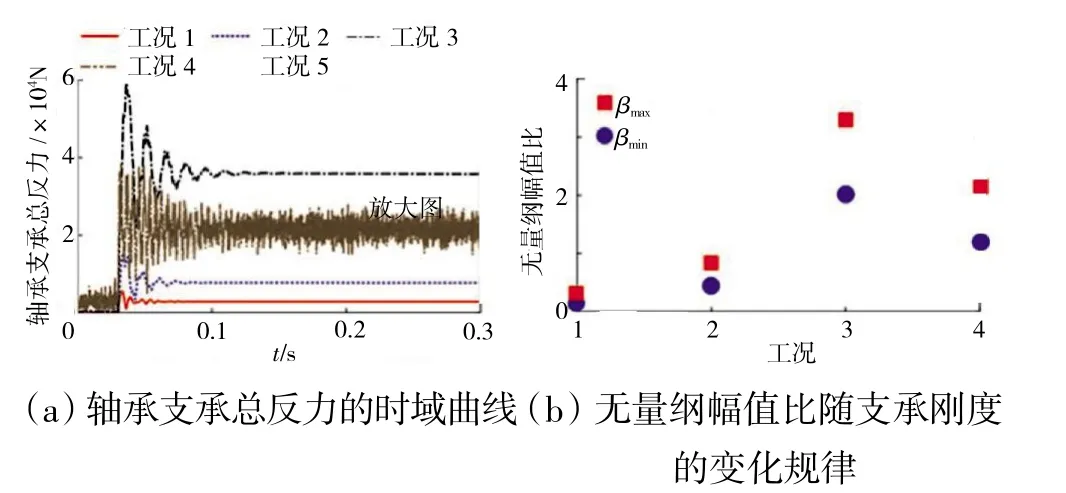
图15 轴承支承总反力的时域曲线以及无量纲幅值比
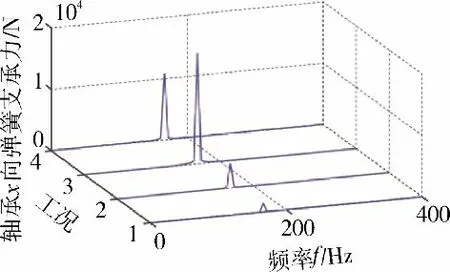
图16 左端轴承x 方向支承反力的3 维谱
4 结论
本文基于ANSYS 和LS-DYNA 软件仿真模拟平台,采用隐式-显式序列相结合的分析方法,建立了弹性支承下转子-盘片系统的有限元模型,并基于此模型讨论分析了转速、不平衡量、盘偏置量和支承刚度对系统振动响应的影响,得到的主要结论如下:
(1)转速越远离系统的近共振区,轴承支承的总反力越小。针对本文所研究的系统,在近共振区的支承总反力幅值放大倍数最高达10 倍以上;
(2)轴承支承总反力的变化趋势与系统不平衡量的变化趋势相同,即随着不平衡量的增加,轴承支承总反力逐渐增大;
(3)轮盘越靠近轴承支承端,叶片飞失引入的轴承支承总反力越小,在转轴中部达到最大值;
(4)在刚性支承下叶片飞失引入的轴承支承总反力较柔性支承的偏大。
