羧酸酯分子结构有限元分析及液体热导率估算

2020-09-15刘万强陆海霞刘凤萍陈冠凡仇明华

高校化学工程学报 2020年4期

刘万强, 陆海霞, 刘凤萍, 陈冠凡, 岳明, 仇明华

(湖南科技大学化学化工学院, 理论有机化学与功能分子教育部重点实验室, 湖南省高校QSAR/QSPR 重点实验室, 湖南湘潭 411201)

1 前言

化学品和材料热导率备受化学化工[1-2]、材料科学[3-4]等领域关注。羧酸酯是羧酸衍生物中的一类化合物，广泛存在于自然界，是香料[5]、油脂[6]、涂料[7]、食品[8]、医药[9]、农药[10]等各领域的原料或产品，其生产加工过程中的温度高低对其性能的影响十分明显。因此，对羧酸酯分子液体热导率数据的掌握有着十分重要的意义。液体热导率较难实验测定，通常多以估算方法获取[11]。如著名的Latini 法[12]、Sastri法[13]、Teja 法和Rice 法等[14]，都只有在对比温度条件下才能进行估算，而Klass 法[15]等都是以基准温度下热导率实验值为前提的。如文献[11]中介绍的Arikol 和Gurbuz 方法，需要以温度、临界温度、临界压力、分子量和标准沸点条件下的液体热导率为前提条件。JAMIESON 和CARTWRIGHT 等[16-17]基于分子结构分析，给出了一个适用温度范围较广的通用估算方程。此后，张克武等[18]基于气体不平衡理论方程推导了液体热导率估算方程。这些方法虽然都将液体热导率的估算与分子结构紧密地联系，但要准确地定量描述分子结构，给出物理意义明确的具体参数值仍然是液体热导率估算方法中的难题[19]。本文将优化构型后的羧酸酯分子结构隐氢图看作是一个无阻尼多自由度振动系统，然后用空间刚架元模型对其进行有限元分析，提取基频、总频、电荷-位移和温度等4 参量构建羧酸酯分子液体热导率估算模型，并由746 个羧酸酯分子液体热导率实验数据得出一个新的估算方程。新方法与著名的Sastri 方法和Latini方法比较，不仅减少估算热导率为前提条件，而且估算值(或预测值)与实验数值之间都表现出很好的一致性，标准误差也都在实验误差范围内。

2 理论与方法

2.1 分子结构空间刚架元模型

图1(a)为邻苯二甲酸二甲酯分子隐氢图，其中包括14个化学键空间刚架元，14个重原子或基团节点。

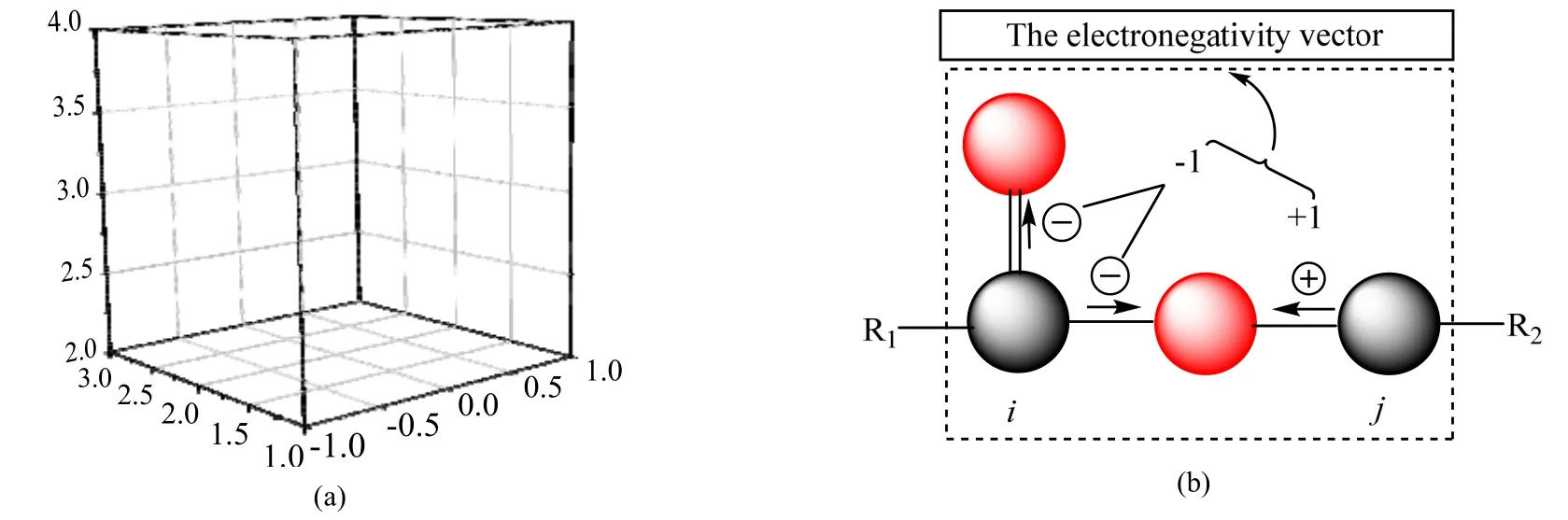
图1 羧酸酯分子结构弹性空间刚架元模型 Fig.1 The space frame element model for the elastomer of carboxylic esters

由文献[20]可知，每个空间刚架元有7 个系数，它们分别是弹性模量E、剪切模量G、惯性矩Ix、惯性矩Iy、极惯性矩J、横截面积A 和长度L，见表1。有关它们的具体计算可参见文献[21-22]。

分子结构空间刚架元分析及模型参量的求解路线如图2 所示。

表1 化学键空间刚架元的6 个系数值 Table 1 Values of elasticity coefficients of chemical bond space frame elements

图2 分子结构空间刚架元分析及模型参量求解路线 Fig.2 Route of model parameters solving for space frame element of molecular structures

2.2 求解分子结构固有频率

从文献[23]可知，当无阻尼多自由度自由振动系统微振方程有非零解时，都对应于一个特征方程，即[K－ω2M]＝0。该方程为矩阵方程，其中K，M 分别是系统的刚度矩阵和质量矩阵。解此方程可确定ω2的n 个正实根ωi2，并按ωi≥ ωi+1排列，i=1, ……., n。这里的ωi就是系统的i 阶固有频率。其中不等于零的最小固有频率称为基频，用“ω0”表示，各阶固有频率之和称为总频，用“∑ωi”表示。有关分子结构固有频率的计算方法和步骤可参考文献[22]，表2 列出了48 个羧酸酯分子结构的振动基频和总频值。

表2 羧酸酯分子结构的基频和总频 Table 2 Fundamental and sum frequencies of the molecular structures of carboxylic esters

2.3 求解电负性差外加载荷下的位移矢量

如图1(b)所示，假设“电负性差”[24]作为外加载荷仅作用于酯基中的i 碳原子和j 碳原子节点上，并指定双键氧原子(C=O)和单键氧原子(C-O)以不同方向作用在i 碳原子上的外加载荷总矢量值为-1，单键氧原子 (O-C)作用在j 碳原子上的外加载荷分矢量值为+1，且i、j 两碳原子节点上的各角度分矢量值均为氧原子的相对质量16。所以i 和j 两碳原子节点上的矢量可用“｛Qi｝”表达，即

式(1)有6 个值，因为每个空间刚架元有6 个自由度，即(x、y、z、α、β、γ)，其中x、y、z 为方向坐标，α、β、γ 为角度坐标。

假设分子中除节点i、j 外，其他不与氧原子有化学键连接的各原子节点均不受“电负性差”外加载荷的影响，即各节点的矢量均为0 矢量，这样就可以写出任何一个分子结构的整体载荷矢量，即

式(2)中省略的都是0 矢量节点。

当弹性体在外力作用下发生变形时，可在所有满足边界条件和协调要求的可能位移中，使总势能为最小[25]，即：

式(3)中：δ 为泛函变分符号，П 为物体的势能，U 是单位体积内总应变能，W 是外力在虚位移上所做的虚功。当单元上受有边界载荷{Z}作用于部分边界时，则按单元计算其应变能和载荷势能，再将两者合起来计算结构总势能[25]，即

式(4)中：∏是离散化后成为节点位移{ }δ 的多元函数；{Q}是全部载荷矢量；[K]是总刚度矩阵，可由式(2)解得；T 为转置矩阵符号。由泛函极值条件可转化为一般多元函数的极值条件，即

若将前已述及的矩阵[K]和载荷矢量{Q } 代入式(5)，即可求出各羧酸酯分子结构在“电负性差”外加载荷作用下的位移矢量{δi}。例如，甲酸甲酯分子的“电负性”外加载荷矢量的表达式为：

{Q}=[-1 -1 -1 16 16 16,0 0 0 0 0 0,0 0 0 0 0 0, 1 1 1 16 16 16]′

其整体刚度矩阵需用Matlab 程序表达和求解[20,22]。

2.4 分子结构电荷-位移参量的定义和计算

当有机分子结构中的重原子是由电负性不同的原子构成时，各重原子的Mulliken 原子电荷矩阵与位移矢量的乘积，即：

式中：qe为分子结构的电荷-位移参量；{δ}为整体分子结构位移矢量；[e]为分子结构各重原子的Mulliken 原子电荷总和。即

式(7)中的ei值来源于分子结构最优化构型的Mulliken 电荷集居分析结果。如甲酸甲酯的Mulliken电荷分布值见表3。

表3 甲酸甲酯分子隐氢重原子Mulliken 电荷总和 Table 3 Sum of Mulliken charges with hydrogens summed into heavy atoms of methyl formate

根据表3的Mulliken电荷总和值可写出甲酸甲酯分子电荷行矩阵，即可求得其电荷-位移参量的值，即：

qe= [e]{δ}= 0.037 0

同理可求得其他羧酸酯分子的电荷-位移参量值，见表4。

表4 羧酸酯分子结构电荷位移参量值 Table 4 Values of charge displacement parameters of the molecular structures of carboxylic esters

2.5 建立羧酸酯液体热导率估算模型

已有的研究结果表明[26]，固有频率中的基频和总频是建立各种定量分子结构-性质/活性相关性(QSAR/QSPR)模型的基础，即

如果在模型(8)的基础上再考虑特定分子结构类型特征，即可得到更理想的QSAR/QSPR 模型，可大大提高羧酸分子定量结构-性质估算模型的相关性，即

式(9)中的λL表示羧酸酯分子的液体热导率；A0表示模型方程的回归常数；A1、A2、A3、A4分别为参量ω0、Σωi、(qeΣωi)和(qeT)的回归系数。

3 结果与讨论

3.1 定量羧酸酯分子结构-性质相关性分析

将表2 和表3 中48 个羧酸酯分子在不同温度条件下的746 个液体热导率实验值及其4 参量值用于模型(9)的回归分析，可得到相应的估算方程，即

式(10)表明，其相关系数r 为0.981 9；标准误差s 为3.778 2 mW·(m·K)-1；样本数n 为746 个；F 检验值为5 000；各参量的灵敏度p 值分别为3.21×10-60、0.000 0；0.000 0 和2.90×10-280。这里的p 值为0 说明该变量与其他变量的关联度非常小，但不是绝对的无关联，因为p 值是一个概率性问题，不是一个确定性问题。各参量的高灵敏性，在估算值与实验值之间存在着良好的一致性，如图3 所示。

图3 计算值和实验值散点图 Fig.3 Scatter plot between calculated and experimental values

3.2 交叉验证与稳定性分析

为进一步考察估算方程(10)的稳定性和可靠性，用留1 法予以交叉验证，其相关性系数为0.981 4，标准误差为3.793 2 mW·(m·K)-1，与回归方程(10)的结果比较，其相关系数仅下降0.000 5，由0.981 9下降到0.981 4，其标准误差由原来的3.778 2上升为3.793 2 mW·(m·K)-1，增大了0.015 0 mW·(m·K)-1。由此可以看出，新方法得到的估算方程(10)不仅具有较高的相关性，而且具有很好的稳定性。

3.3 温度对羧酸酯液体热导率的影响

从模型方程(10)中可以看出，(qeT)项的系数虽然为负数，但不能表明羧酸酯的液体热导率随温度的升高而直线下降。因为大多数液体在接近熔点、沸点、特别是临界点时的热导率随温度的变化会明显变缓，所以严格来说，液体的热导率随温度变化的线性关系只能在相对温度范围内近似成立，如熔点到沸点之间较宽的温度范围内，可近似地满足线性关系。因此，用模型方程(10)估算羧酸酯的液体热导率时，在接近熔点或沸点温度10～20 ℃，可能会产生一定的误差。

3.4 电荷-位移参量的定义及其对羧酸酯液体热导率的影响

电荷-位移参量qe在模型方程(9)中是以各阶固有频率之和(Σωi)与绝对温度T 的乘积(qeT)的形式出现，在估算方程(10)中可以看出，参量(qeΣωi)的运算符号为“+”，而参量(qeT)的运算符号为“-”，且其中的T一般来说总是会大于Σωi，两者的共同结果应该是同温同压下，羧酸分子的液体热导率数值的大小似乎与qe值的大小成反比。但实际上并不是如此，因为估算方程(10)中总频参量(Σωi)的运算符为“-”，这与复合参量(qeΣωi)中参量Σωi的运算符号是相反的。所以在考虑qe的影响时要与总频Σωi参量综合考虑。