高速铁路轮轨声辐射特性研究

2020-09-15步青松周卫军伍向阳陈迎庆

铁路节能环保与安全卫生 2020年4期

步青松，周卫军，伍向阳，陈迎庆，邵琳

（1. 中国铁道科学研究院集团有限公司节能环保劳卫研究所，北京 100081；2. 中国国家铁路集团有限公司发展和改革部，北京 100844）

国内外高速铁路噪声源识别结果表明，轮轨区域噪声源，尤其是轮轨滚动噪声是最重要的噪声源之一[1-3]，车轮和钢轨是轮轨滚动噪声最主要的发声部件，直接决定着轮轨滚动噪声的辐射水平。KURITA T 等[4]、BENDER E K 等[5]、TOMPSON D J 等[6-9]、REMINGTON P J[10-12]从车轮和轨道的简化模型出发，建立计算模型，预测轮轨振动和声辐射，并逐步发展成为TWINS工程化应用软件；徐志胜[13-14]、翟婉明[15]、杨新文等[16-17]结合轮轨垂向动力学和声辐射理论，采用半解析振动-声辐射效率公式计算轮轨系统的振动声辐射特性，逐步建立轮轨滚动与冲击噪声预测的统一模型(WRNOISE)。本文针对高速列车运行时的典型工况，即径向激励下的车轮和钢轨动力特性进行仿真分析，通过建立有限元-边界元混合模型，研究径向激励下轮轨声辐射特性。

1 建模分析

轮轨滚动噪声既与列车运行速度、运行线路类型等工况参数有关，又与轮轨接触区导纳特性、车轮悬挂参数、钢轨支撑特点和轮轨本身结构特性等多体动力学拓扑特点有关。

1.1 车轮有限元-边界元模型

以某型号动车组拖车车轮为研究对象，建立车轮有限元模型，车轮模型采用三维实体单元，在轮毂孔位置施加固定约束。车轮为直辐板结构，名义滚动圆直径为920 mm，轮毂孔直径为186 mm，弹性模量为210 GPa，密度为7.85 kg/m3，泊松比为0.3。车轮有限元模型共建立实体单元数为15 330个，对应的节点数为17 123个，定义车轮竖直径向为X轴、水平径向为Y 轴、车轮轴向为Z 轴，车轮边界条件及有限元模型如图1所示。

将车轮位移导纳结果作为声学分析的位移边界条件，建立车轮边界元模型如图2 所示。采用直接边界元法求解边界封闭外声场的Helmholtz 波动方程，计算车轮的振动声辐射特性。计算中，空气中的声速为344 m/s，空气密度为1.21 kg/m3；边界元网格中最大单元边长小于计算频率波长的1/6，以达到要求的分析精度，为避免轮毂孔位置产生声泄露，将轮毂孔位置采用单元封闭。

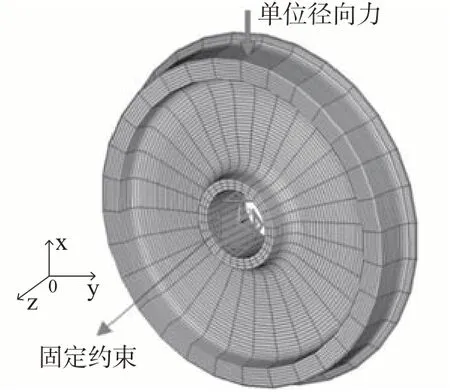
图1 车轮有限元模型

图2 车轮边界元模型

1.2 轨道有限元-边界元模型

以设计速度为350 km/h的某高速铁路无砟轨道直线区段参数为研究对象，构建包括钢轨、扣件系统、轨道板的合理简化有限元-边界元分析模型，考虑轨道结构的纵向对称特征，取轨道结构的一侧建立长度为6.5 m 的轨道系统模型，根据动力计算的效率和稳定性对各部分网格尺寸进行匹配。钢轨和轨道板采用三维实体单元模型，扣件系统采用非线性弹簧单元模拟，以等间隔离散支撑方式连接钢轨和轨道承轨台，以沿钢轨纵向中部为基准，以转向架轴距2.5 m 为间隔施加单位简谐力。钢轨离散支撑有限元模型共建立实体单元数为52 380 个，对应的节点数为68 523 个，定义轨道竖直方向为X轴、纵向为Y轴、垂直于钢轨的水平方向为Z轴，有限元模型如图3所示。

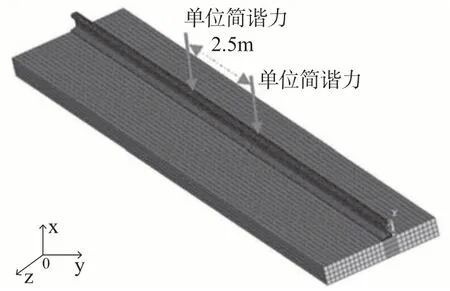
图3 钢轨离散支撑有限元模型

采用包络网格建立钢轨的声学网格，与有限元模型计算得到的钢轨表面振动数据建立耦合关系，轨道结构周围空气介质参数、单元网格参数和计算设置与车轮边界元分析模型一致，构建声学边界元模型如图4所示。

图4 钢轨离散支撑边界元模型

2 数值计算和结果分析

2.1 车轮声辐射特性

以高速列车在直线区段运行为典型工况，在车轮滚动圆位置施加径向单位正弦力激励，计算高速列车车轮的频响特征，对显著频率下的车轮声辐射功率进行分析，各频率下车轮声功率级和1/3 倍频程声功率级如图5所示。

由图5 可见，在单位径向力激励下车轮声功率随激励频率变化波动较大，这主要与车轮柔体模态在不同频率下本征特征有关；车轮声功率在中低频随频率提高快速增大，但总体在800 Hz 以内声级水平较低，800 Hz以上声级水平较高。主要原因在于车轮声辐射效率，车轮属于小尺度发声部件，低频辐射效率低，声辐射效率总体而言随频率提高而提高，高频声辐射效率趋近于1。

车轮作为高速铁路对周围环境产生影响的重要噪声源，以往研究车轮噪声传播特性时，一般将车轮简化为点声源，仅能近似用于远场噪声预测，而近场、远场界定通常需结合声源尺寸、所关注声波波长及距离确定。对于车轮和钢轨而言，钢轨通常可视为直径为钢轨高度的系列声源组成，因而车轮和钢轨声源辐射面半径a均小于0.5 m，而轮轨辐射噪声主要峰值频率一般为200~2 000 Hz，对应声波波长λ约为0.2~1.7 m，声波波数k=2π/λ，声源至预测点的距离为r。基于波动声学研究表明：ka≪1时，可以忽略声源尺寸的影响，kr≫1时可以忽略近场声源指向特征。因此，本文对应不同声波频率统一界定距离声源5 m 内视为近场，大于5 m的范围视为远场。

由于车轮自身结构拓扑结构特点，在各响应频带存在不同的结构体振动特征，尤其是近场声辐射特性与车轮结构振动特点密切相关，通过建立车轮声辐射三维平面场，研究车轮近场声辐射特性。以车轮为原点，车轮运行方向为参照线，分别建立XY 竖直垂直平面、XZ竖直纵向平面和YZ水平平面，平面长宽皆为5 m，分析结果如图6所示。

由图6 可见，随着激励频率升高，车轮声辐射在3 个平面内的主旁瓣特征显著增强，在图6 中表现为以车轮为圆点的同一圆周方向的颜色波动剧烈程度加强，这与车轮结构体表面振动的模态特征随频率升高振动形态更加复杂相关；同时，随着距车轮距离的增加，其声场云图分布颜色越来越均匀，车轮声辐射指向性减弱。由此可见，车轮声辐射在近场分布与其振动形态密切相关，近场主旁瓣特征和指向性较为明显。

在高速铁路车轮各向辐射声场中，距线路不同距离的声场分布特性对环境噪声的影响最大。因此，为了进一步研究车轮远场声辐射特性，更好地支撑高速铁路环境噪声预测，建立与轨道面平齐的距线路中心线30 m、沿线路方向5 m的声场水平平面分布，如图7 所示，图中横坐标为距线路水平距离(从右至左30 m)，纵坐标为沿线路长度方向5 m。

由图7可见，在所给出的100 Hz、500 Hz、1 000 Hz、2 000 Hz、3 000 Hz 和5 000 Hz 激励频率下车轮声场分布云图中，车轮噪声在近场主旁瓣颜色波动变化显著，表明近场噪声具有较强的指向性；随着距车轮距离增大，辐射噪声的指向性逐渐减弱；在距车轮水平距离30 m处(图中最左侧)其声场分布基本达到均匀状态。因此，在高速铁路轮轨滚动噪声远场预测中，将单个车轮简化为点声源的做法可行。

综上，随着激励频率升高，在3 个平面内车轮声辐射主旁瓣特征显著增强，主要原因在于车轮结构体表面振动模态特征随频率升高振动形态更加复杂；同时，随着距离增加，车轮噪声强指向特性明显降低。由此可见，车轮近场声辐射与振动形态密切相关，近场主旁瓣特征和指向性较为明显，因而基于点声源预测计算轮轨滚动噪声源是不合理的，但用于预测远场不同距离噪声衰减量是可行的。

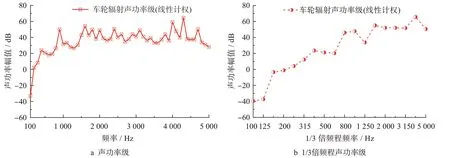
图5 车轮声功率级

2.2 钢轨声辐射特性

与车轮的声辐射特性分析工况类似，以高速铁路无砟轨道的有限元-边界元模型为基础，对离散支撑的6.5 m 长钢轨进行振动计算并导入声学软件进行声辐射分析，在钢轨中部单侧转向架的2 个车轮对应位置施加单位正弦简谐激励(见图3)，计算单块轨道板上的钢轨声辐射特性，各频率下钢轨声功率级和1/3 倍频程声功率级如图8所示。

由图8 可见，两点单位简谐力激励下钢轨声功率随激励频率提高波动也较大，与钢轨自身结构特点和约束支撑参数导致的振动模态特征密切相关；在250 Hz 以内钢轨声辐射水平较低，之后随频率逐渐升高，1 600 Hz 及以上频率声功率保持在相对较高水平。

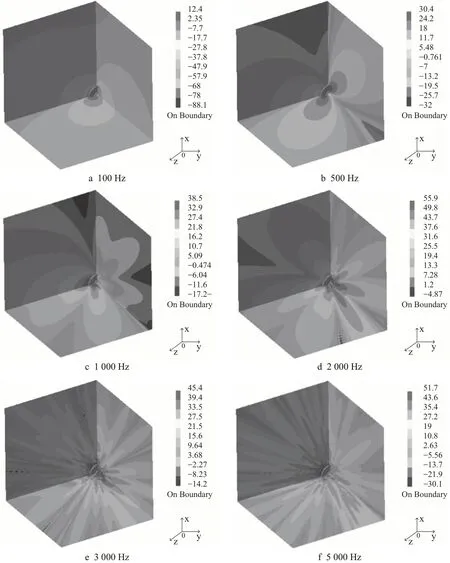
图6 单位径向力作用下车轮辐射三维声场近场分布

由于高速铁路钢轨可视为无限长，与车轮近似移动点声源特征不同，钢轨受到激励后振动会沿钢轨自身纵向传递。高速列车通过前后，在一些敏感频带存在振动纵向传递产生、持续时间较长的声辐射现象，从声源尺度和持续时间角度对环境噪声的影响可能比车轮更严重。对钢轨在三维声场中的声辐射特点进行研究(如图9 所示)，以钢轨中部为原点，钢轨纵向为参照线，分别建立XY竖直纵向平面、XZ竖向垂直平面和YZ 水平平面，平面长宽皆为5 m，针对典型频率，分析钢轨近场三维声辐射特点。

由图9 可见，钢轨近场声场分布主旁瓣波动特征在竖直纵向XY 平面内最显著，主要是由于钢轨离散支撑于轨道板之上，XY 平面内钢轨沿纵向刚度不均匀性最大引起。波动特征在水平平面YZ 内次之，对应于钢轨横截面XZ 平面内波动最小。这充分表明钢轨近场声辐射同样存在较强指向性，计算钢轨声源声功率直接采用无指向性线声源显然是不合适的；随着距离增加，声辐射指向性减弱。

为了进一步研究钢轨远场声辐射特点，与车轮远场声辐射特性分析一致，建立与轨道面等高、距线路中心线30 m(横向)、沿线路方向5 m(纵向)的声场水平平面分布，如图10所示。

图7 单位径向力作用下车轮辐射声场远场分布

图8 钢轨辐射声功率级

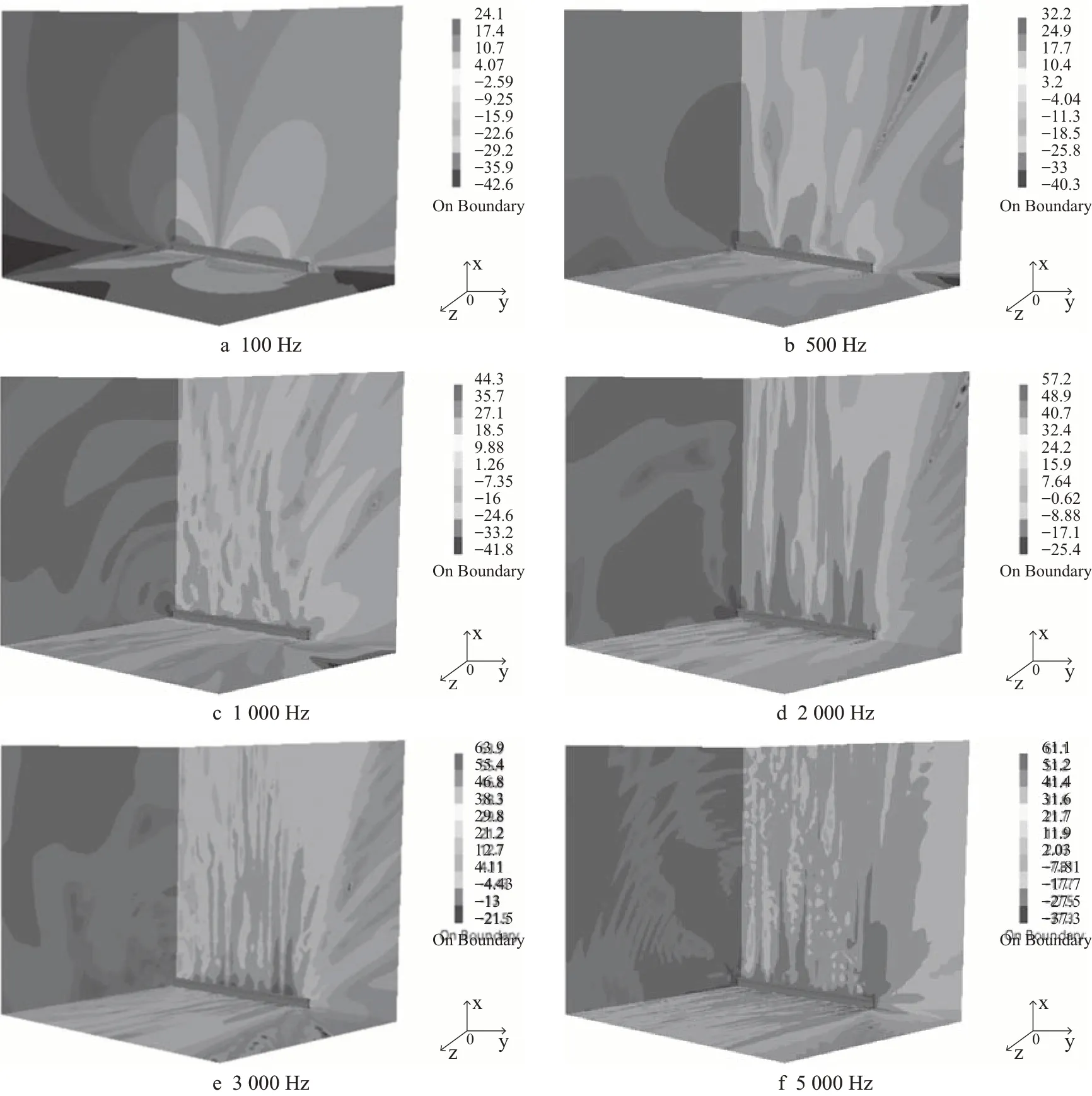
图9 钢轨辐射三维声场近场分布

由图10可见，激励频率为100~5 000 Hz时，钢轨辐射噪声在近场指向性显著，随着距线路水平距离增加，辐射噪声的指向性明显减弱，在距钢轨水平距离30 m 处(图中最左侧)声场分布也基本达到均匀状态。因此，在高速铁路轮轨滚动噪声远场预测中，将钢轨噪声简化为线声源计算不同距离噪声衰减量的方法也是可行的。