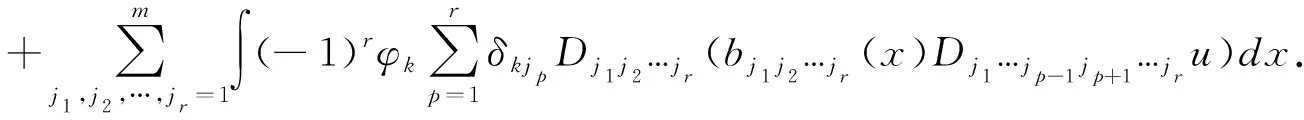高阶一致椭圆型算子第二特征值上界估计的不等式

赵晓苏，钱椿林

(苏州市职业大学数理部，江苏 苏州 215104)

1 本文主要结果

设Ω⊆Rm(m≥2)是有界区域，Ω具有逐片光滑的边界∂Ω，考虑下列特征值问题：

(1.1)

μ1≤ai1i2…is(x)≤μ2，i1,i2,…,is=1,2,…,m

(1.2)

v1≤bj1j2…jr(x)≤v2，j1,j2,…jr=1,2,…,m

(1.3)

其中0<μ1≤μ2，0

关于问题(1.1)的等号两边都是调和算子的第二特征值估计，目前已有结果，问题(1.1)的等号左端是一致椭圆型算子，等号右端是调和算子的第二特征值估计，也已有结果，问题(1.1)的等号左端是四阶一致椭圆型算子，等号右端是二阶一致椭圆型算子的第二特征值估计，可参见文献。问题(1.1)的等号左端是高阶一致椭圆型算子，等号右端r是二阶一致椭圆型算子的第二特征值估计。在本文中，研究问题(1.1)的等号左端是高阶一致椭圆型算子，等号右端是r阶一致椭圆型算子。将文献[1]中的问题进一步推广，并文献[2]中的方法加以改进，对于问题(1.1)得到了可由第一特征值来估计第二特征值上界的估计不等式，并且估计的系数与区域度量无关，所得结果在力学和微分方程的研究中有着广泛的应用。

定理 设λ1，λ2是问题(1.1)的两个第一、第二特征值，且0<λ1<λ2，则有

(1.4)

2 定理的证明

(2.1)

利用分部积分和(2.1)，得

(2.2)

利用分部积分和(2.2)，有

(2.3)

利用(1.2)和(2.3)，得

(2.4)

利用(1.3)和(2.2)，有

(2.5)

设

φk(x)=(xk-qk)u

其中

式中

利用分部积分，直接计算得

(2.6)

(2.7)

从(2.7)知，φk与u带权正交，且满足

利用Rayleigh定理，成立着

(2.8)

计算得

(2.9)

式中

利用分部积分和φk(x)=(xk-qk)u，有

(2.10)

结合(2.9)和(2.10)，得

(2.11)

设

利用式(2.11)，有

(2.12)

利用(2.8)和(2.12)，有

(2.13)

设

引理1：设u是问题(1.1)所对应第一特征值λ1的特征函数，则

证：对于(a)，利用数学归纳法，当t=1时，等式(a)显然成立。假设对t=k等式(a)也成立。

当t=k+1时，由归纳假设，可得

故引理1(a)成立。

对于(b)，继续使用归纳法，t=1时，利用(2.5)的右端，不等式显然成立。假设t=k时，不等式成立，即有：

当t=k+1时，利用分部积分、Schwarz不等式和归纳假设，得

化简整理，有

即引理1(b)成立。

对于(c)，反复运用引理1(b)及(2.4)式，得

由引理1(a)及(2.4)式，有

(2.14)

引理2：设u是问题(1.1)属于第一特征值λ1的特征函数，则

证：关于(a)，由引理1(a)、(c)及(2.5)式和Schwarz不等式，可得

整理后引理2(a)成立。

对于(b)，利用(1.3)，引理1(a)和Schwarz不等式，有

即引理2(b)成立。

对于(c)，利用(1.3)，引理1(a)和引理2(a)，当p≠q时，有

同样的，当p=q时，得

故，有

故引理2(c)得证。

引理3：在引力2的假设下，有

证：对于(a)，利用(1.2)和Schwarz不等式，得

当p≠q时，利用引理1(a)和引理1(c)，取t=s-1，有

类似地有

当p=q时，同样可得

所以，得

对于(b)，利用Schwarz不等式，引理1(a)和引理1(c)，类似地，有

引理4：设是问题(1.1)的第一特征值，则

证：利用分部积分和φk(x)=(xk-qk)u，得

(2.15)

利用分部积分，得到

(2.16)

(2.17)

利用(2.15)、(2.16)和(2.17)，有

(2.18)

利用(2.18)，引理2和引理3，得

引理5：对于φk与λ1(k=1,2,…,m)，有下列不等式成立

证：利用分部积分和φk(x)=(xk-qk)，得

(2.19)

利用(2.19)，有

(2.20)

利用(2.20)和(2.5)，有

(2.21)

利用(2.21)、(1.3)、引理1(c)和Schwartz不等式，得

由上式引理5得证。

定理的证明：由引理4、引理5及(2.13)，可得

经整理即得定理。