基于零膨胀模型的高速公路事故形态影响因素分析
2020-09-15王羽尘马健霄刘宇航白莹佳
王羽尘,陆 涛,马健霄,刘宇航,白莹佳
WANG Yuchen, LU Tao, MA Jianxiao, LIU Yuhang, BAI Yingjia
(南京林业大学 汽车与交通工程学院,江苏 南京 210037)
(College of Automobile and Traffic Engineering, Nanjing Forestry University, Nanjing 210037, China)
0 引 言
高速公路由于其同向性、便捷性以及舒适性等优势[1],在国家公路网中起着至关重要的作用。据统计,2018 年我国高速公路里程达到14.26 万公里,每年有近5%左右的增幅[2]。由于高速公路的行驶要求、复杂的路况环境等因素,一旦发生事故,易造成交通拥堵,产生次生事故,带来更大的伤亡和损失。通过研究不同因素对事故形态的影响程度[3],可以从不同角度分析事故成因,对于减少轻微交通事故和降低重大事故的人员伤亡、财产损失具有重要的意义。
由于交通事故数据大多具有离散度不足(低扩散)、低密度(数据的样本均值较低) 等特征[4],国内外学者利用数学模型围绕事故发生的道路、环境及车辆等因素与交通事故形态的关系进行系统研究,通过分析数据分布特征并选用与之匹配的模型,可以降低参数估计的误差,精确刻画不同因素对事故形态的影响。通过整理不同文献,得到不同模型以及其适用条件和不足,归纳总结如下:
(1) 当数据特征为非负整数时,常采用泊松分布模型和负二项/泊松-γ 分布模型,此类模型易于估计,且后者可以应用于过度离散的情况,但无法描述离散度不足、低密度、样本量少的情况。Xie 利用贝叶斯Logit 模型研究驾驶人特征、碰撞车辆以及道路条件对事故形态及严重程度的影响[5]。马聪从事故发生地点、道路条件、车辆类型3 个方面改进非线性负二项预测模型[6]。
(2) 当数据特征为大量零值时,常采用零膨胀泊松和零膨胀负二项,后者可以处理0,1 的数据集,但无法应用低密度、小样本的情况。李蕊选取道路、环境、驾驶员及车辆等因素,将零膨胀模型应用于高速公路交通事故严重程度分析[7]。
(3) 当数据特征为多组因变量时,常采用二元模型和多元模型,后者因变量范围更广,估算过程复杂。
(4) 任何数据类型都可以使用机器学习进行分析,但估算过程复杂,没有可解释的参数,无法转移其他数据集。Li 选择事故发生地点、车辆类型、道路条件作为影响因素,比较SVM 和多元模型的适用性[8]。
综上所述,国内外学者大多集中于不同数据及模型的适用性,但是对因素本身的关注不够,未考虑影响因素作为模型的自变量,在周期内的潜在变化可能导致重要信息的丢失。因此,本研究收集了连续4 年的高速公路事故数据,选取道路、环境及车辆指标,通过分析数据的分布类型,选取合适的模型,探究影响因素的年时变特征。
1 数据描述
本文所用高速公路事故数据来自沪蓉高速(G42 江苏段),桩号为k36+000-k192+000,每起事故均包含事故发生的时间、地点、事故形态、道路线形及车辆等信息,剔除信息记录不完整的事故,最终用于本研究的事故总数为2 098 起。根据事故记录数据,从高速公路道路条件、环境、车辆信息3 个等方面选择了4 个自变量,具体说明如表1 所示。
根据4 年内的统计数据,选取事故形态作为因变量。将碰撞、刮擦、翻车作为主要事故形态,碾压、坠落、爆炸和失火作为其他事故形态进行研究,如图1 所示。
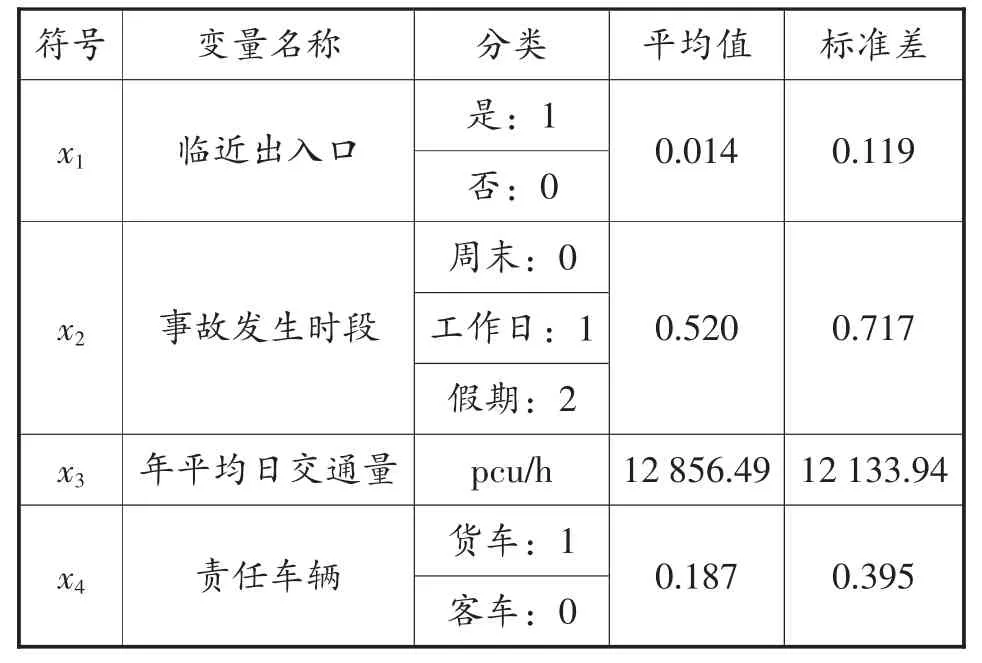
表1 自变量统计及符号
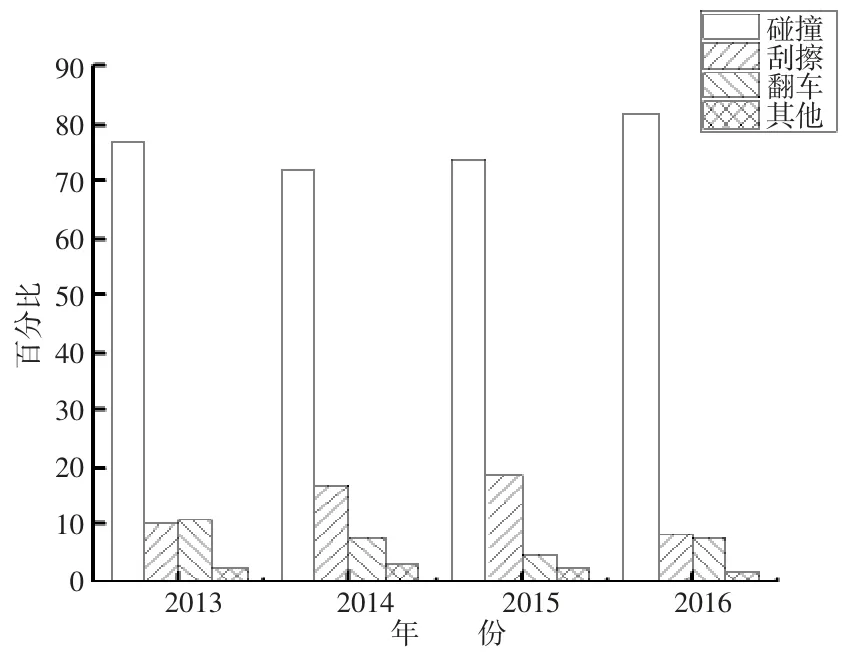
图1 事故形态频率分布柱形图
2 模型建立
由于数据中零值居多,相比于传统的数学计算模型,零膨胀模型可以更加准确地描述此类数据。陈颖雪、曾平将零膨胀模型分别应用于轨道触网故障频次[9]、心肌缺血节段数的研究中[10]。因此,本文采用零膨胀模型中运用最广泛的零膨胀泊松(ZIP)和零膨胀负二项(ZINB) 模型分析不同事故形态的主要影响因素,选用似然比(LR) 检验比较两个模型的拟合程度。
2.1 零膨胀模型
零膨胀模型是由伯努利分布和普通计数分布按照一定比例组成的混合分布[11],当零膨胀模型应用于事故形态研究时,可以理解为发生n起交通事故中,若第i种事故形态事故发生的次数Yi服从结构零权重为φi的零膨胀模型,其概率分布函数为:

式中:Ki为基本计数分布,φi为第i起事故中出现过多0 所占的比例,其取值为0<φi<1。

式中:νi=(νi1,νi2,…,νiq)为q×1 协变量向量,表示第i起事故中q个影响因素的取值,α=(α1,α2,…,αq)为q×1 参数向量,q为协变量个数。
对零膨胀模型中结构零权重φi作回归,得到式(3):

式中:φi,νi,α 意义同上。
2.1.1 零膨胀泊松模型
当Ki服从Poisson 分布,选取影响因素作为分布均值λi的自变量[12],即:
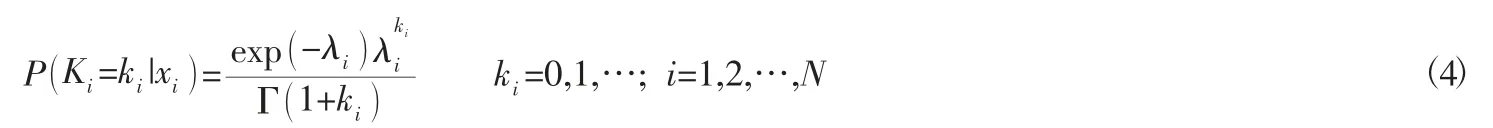
其对数似然函数为:
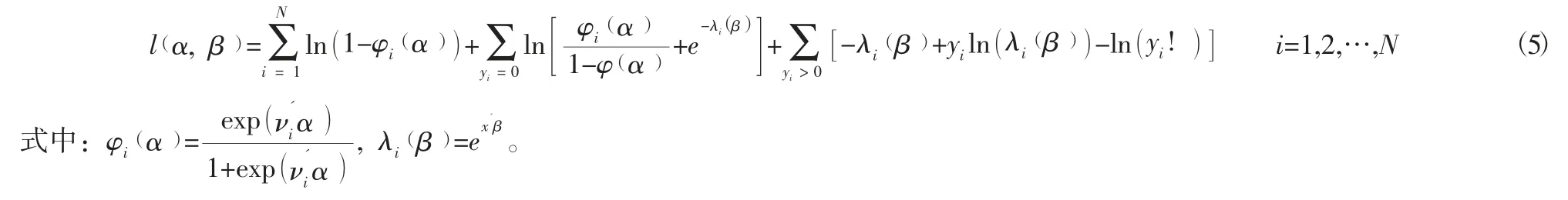
分别对 α=(α1,α2,…,αq),β=(β1,β2,…,βp)求偏导,并令其等于零可求得参数估计值
2.1.2 零膨胀负二项模型
当Ki服从负二项分布,选取主要影响因素作为分布均值μi的自变量,即:
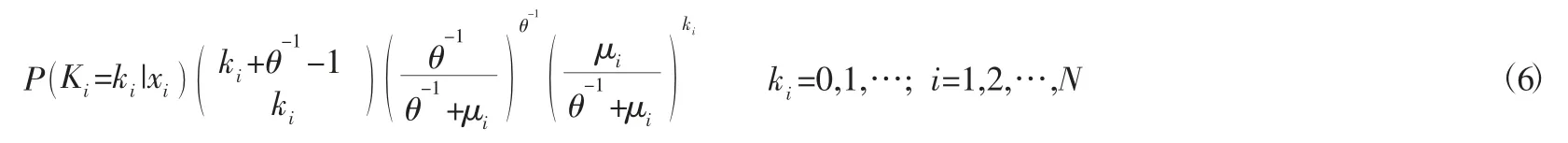
其对数似然函数为:
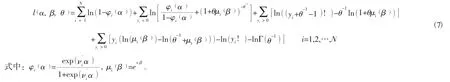
分别对 α=(α1,α2,…,αq),β=(β1,β2,…,βp),θ 求偏导,并令其等于零可得到参数估计值
2.2 模型检验方法
若两个模型的全部自由参数都是相同的,并且其中一个模型可通过限定部分参数为固定值而得到另一个模型,则称其中一个模型嵌套另一个模型[13]。当零膨胀负二项模型中的离散参数θ=0 时,模型即退化为零膨胀泊松模型。
因此,可以使用似然比检验的方法对模型进行选择,先假设零膨胀泊松模型嵌套零膨胀负二项模型,对应的似然比统计量为:

式中:LR服从自由度为ν 的卡方分布,L1为零膨胀泊松模型,L2为零膨胀负二项模型ν=df1-df2为受限参数的个数,在这里为1。若则可表明零膨胀负二项优于零膨胀泊松模型[14]。
3 结果分析
将不同事故形态作为因变量,影响因素作为自变量,建立零膨胀泊松模型和零膨胀负二项回归模型。根据LR指标来判断模型拟合的优劣,采用Python 编程得出各影响因素的估计系数和显著度指标P值,如表2~5 所示。
3.1 模型比较与选择
3.2 影响因素分析
3.2.1 显著度分析
根据显著度指标p值是否小于0.05 可以得出不同因素对事故形态的影响,若小于0.05,则说明该因素对模型影响显著,当p值越接近零,说明检验程度越好。因此,得出以下结论:
以2016 年的事故数据为例,事故发生时段对碰撞和翻车这两类事故形态影响显著,临近出入口和年平均日交通量对所有事故形态影响显著,当交通量发生变化时,交通流状态和车辆间的相互影响也随之改变,导致交通冲突和事故的发生。相比于责任车辆为小型车辆,货车等大型车辆对碰撞、刮擦、翻车这3 类事故形态影响更为显著。
3.2.2 时变特征分析
通过模型结果得到各影响因素系数随时间变化趋势图,如图2 所示。
对比图2(a) 可以看出:事故发生时段对翻车和其他事故起着反向作用,潜在原因是:工作日期间,驾驶人警惕性提高,车辆减速行驶;假期期间,交通量激增,交通流达到稳定反而降低了事故的严重程度。
临近出入口对碰撞和翻车和其他事故起到反向作用,如图2(b) 所示。可能原因是隧道等特殊路段存在着视距不足、平面线形指标较差等原因,导致安全事故发生。近年来对路段的出入口段进行排查和整治,降低了车辆相互碰撞、撞击隧道洞口和翻车的概率。但是,该研究结果尚需进一步验证和研究。
从图2(c) 可以看出,随着年平均日交通量的递增,碰撞、刮擦、翻车这3 类事故形态的系数也在整体增长。特别的是,刮擦事故自2013 年系数递减之后,在2015 年开始递增。这是由于交通流达到稳定前,较小交通事故或行车障碍的影响容易消除,而突破稳定流范围下限之后,交通流稍有增加就会导致服务水平显著降低。
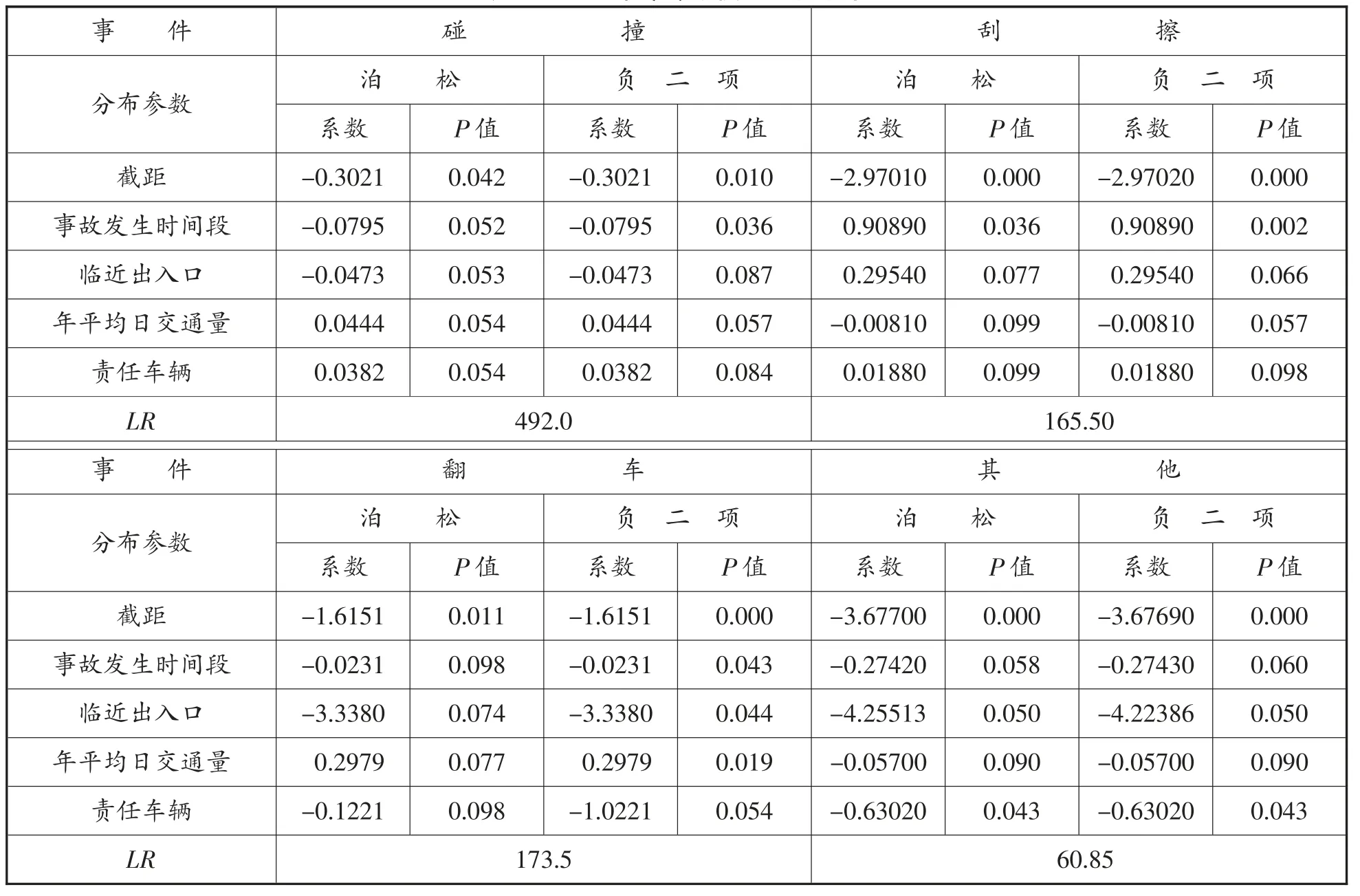
表2 2013 年零膨胀模型分析结果
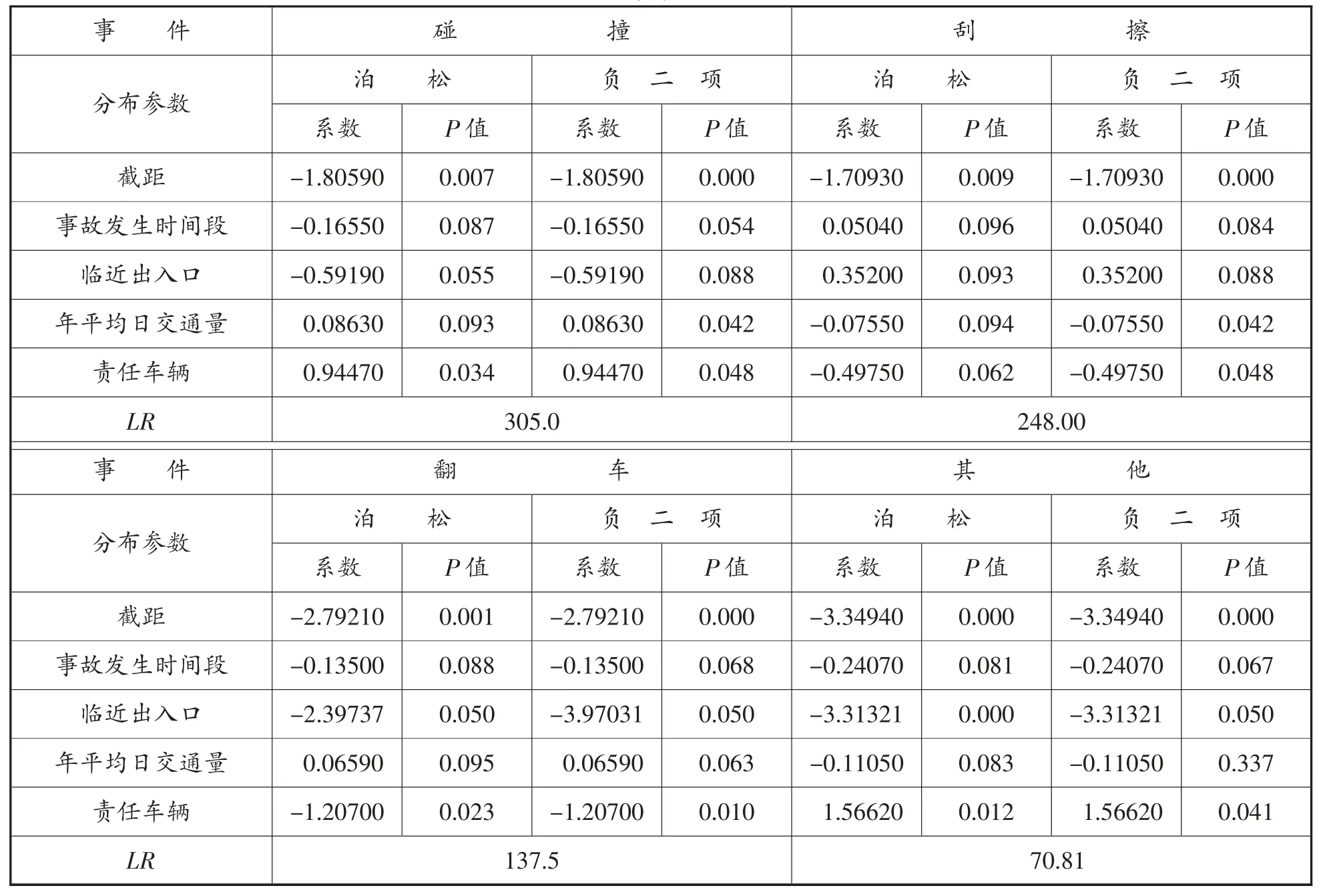
表3 2014 年零膨胀模型分析结果
责任车辆为大型车时,各类事故呈现上升趋势,如图2(d) 所示。潜在原因是大型车受到动力和车辆性能的影响,其初始运行速度未能短时间内达到设计速度,小型车因其功率和重量的比值较大,能够短时间内达到道路的设计速度,两种车型之间存在速度差,从而造成不同类型的交通事故频发。
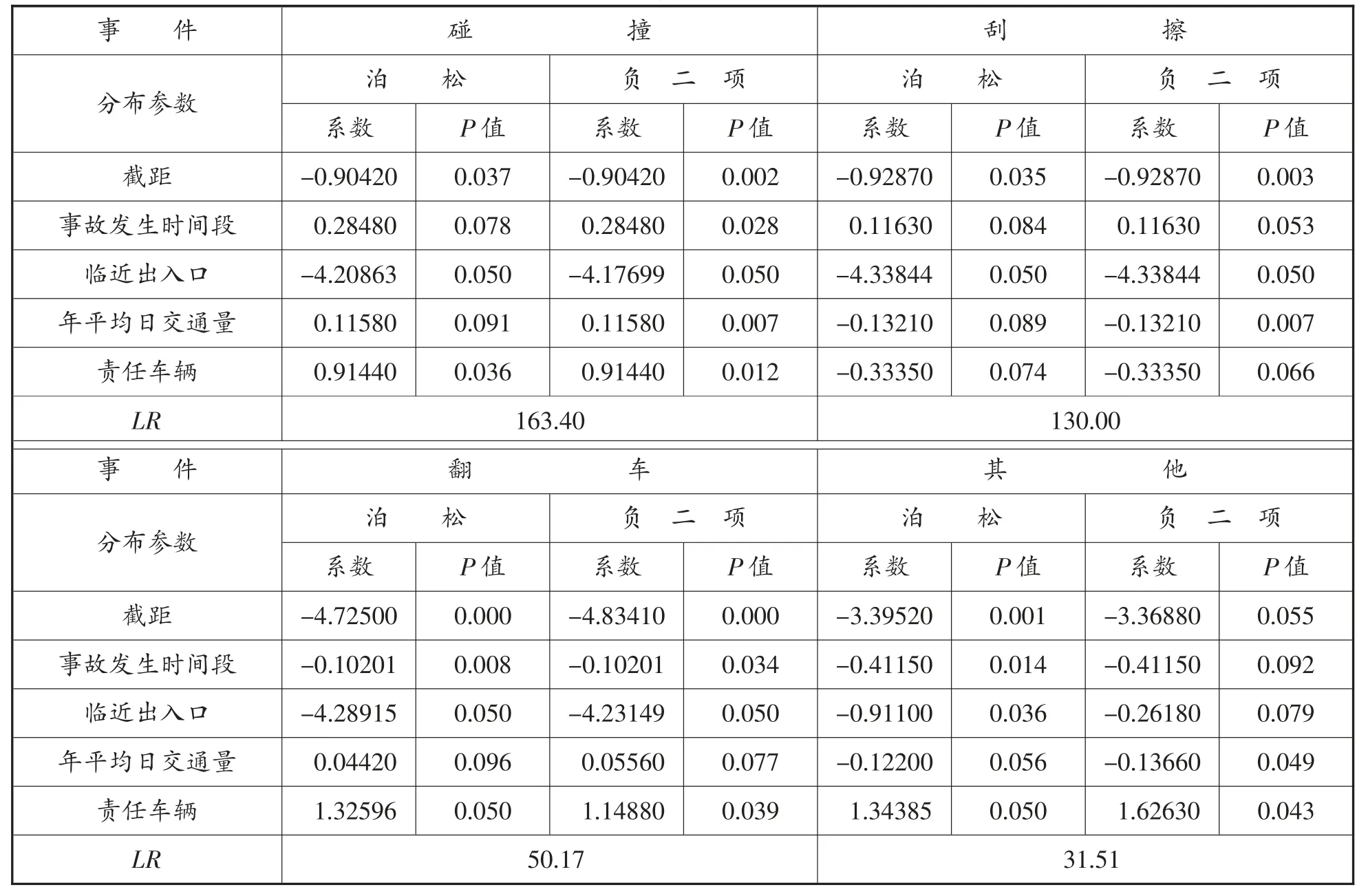
表4 2013 年零膨胀模型分析结果
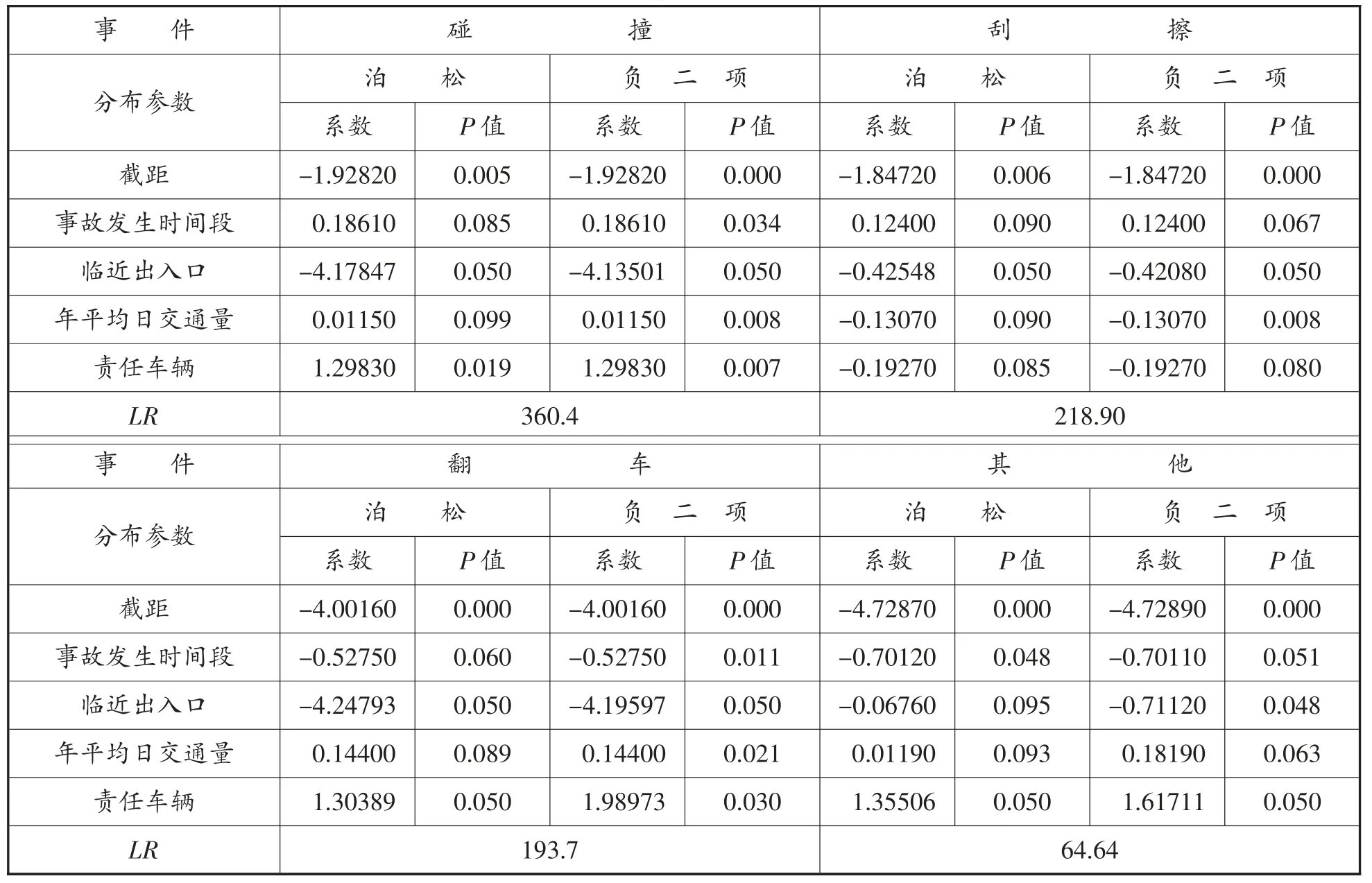
表5 2016 年零膨胀模型分析结果
4 结 论
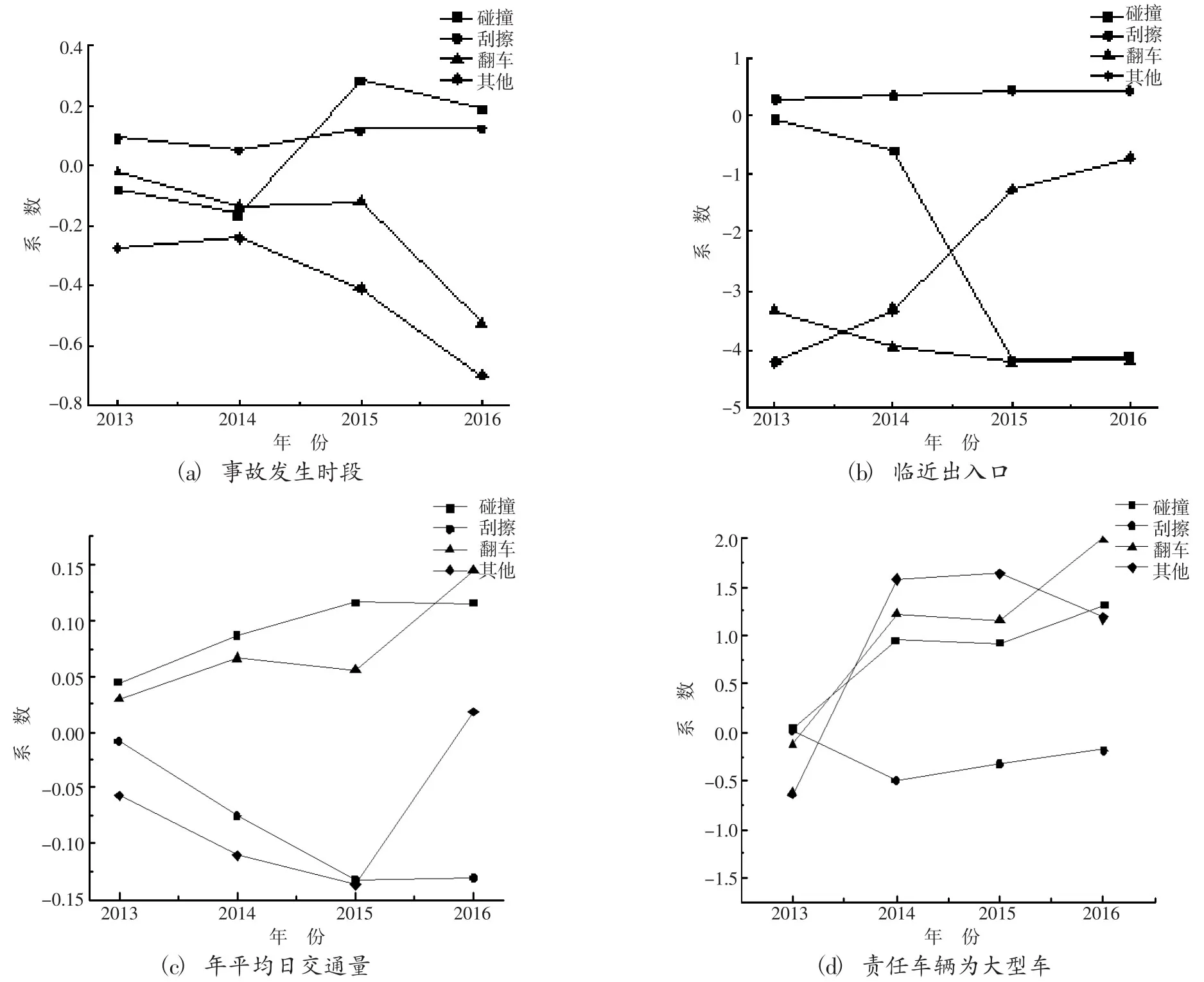
图2 影响因素的时间变化
(1) 基于2013~2016 年沪蓉高速(G42 江苏段) 的事故数据得到影响事故形态的各因素,建立零膨胀模型,并用似然比验证零膨胀泊松和零膨胀负二项模型的拟合程度。从显著度和时间变化趋势两个角度分析不同因素对事故形态的影响。结果表明,零膨胀负二项模型拟合度更好。
(2) 研究结果可以为相关管理人员降低不同事故形态风险提供理论依据,由于数据来源有限且存在部分数据缺失的情况,本研究仅考虑4 个因素对事故形态的影响,后续可针对不同路段研究其他因素对发生事故形态的影响。
