考虑灾民有限理性的应急物资分配模型及算法

陈 刚 （贵州大学 管理学院，贵州 贵阳 550025）

CHEN Gang (School of Management, Guizhou University, Guiyang 550025, China)

由于近十几年来突发性自然灾害的频繁发生，应急物流受到国内外学者的广泛关注，其中应急资源分配问题又是研究的热点之一。例如Yu 等[1]以总成本最小为目标，构建了一个多阶段的应急物资分配模型，其中成本包括可达性成本、损失成本以及惩罚成本；Ransikarbum 等[2]在考虑物流网络部分设施被毁情况下，构建了一个以公平最大、未满足需求最小、成本最小为目标的应急资源分配模型；宋晓宇等[3]以最小化总成本和最大化受灾点满意度为目标，构建了一个多受灾点、多出救点和多阶段的非线性连续消耗应急物资调度模型；黄辉等[4]研究了灾害初期多品种应急物资配比包装调运的两阶段模型，第一阶段以时间效益最大为目标，第二阶段以满意度最大为目标；陈刚等[5]构建了同时考虑应急物资分配公平与效率的多目标优化模型。

综上所述，学者们大多采用经典的运筹学方法，建立以成本最小、时间最短或需求满足率最大等效用函数为目标的优化模型。但事实上，实证研究和仿真实验已经证实人是有限理性的[6]，存在参考依赖、公平关切等行为[7]。随着移动互联网的普及，灾民能够迅速获得应急救援的相关信息，如果灾民对资源分配结果存在质疑，有可能引起舆论效应，甚至影响社会稳定。鉴于此，本文构建考虑灾民感知满意度的效用函数，在此基础上运用前景理论的价值函数对灾民的有限理性进行刻画，以总价值最大为目标，建立供不应求情况下的整数非线性规划应急物资分配模型，设计相应的求解算法，通过实际案例分析验证模型和算法的可行性和实用性。

1 灾民有限理性行为分析

应急救援初期所能利用的应急资源有限，应急物资往往供不应求，灾民不清楚何时能得到救助，以及分配得到的应急物资是否满足需求。对此，灾民表现出有限理性行为，对获得救援的时间以及应急物资的分配数量十分敏感[8]，同时存在参考依赖及公平关切等行为。因此，本文以时间参考点和需求参考点的加权效用作为价值函数的参考点，运用前景理论的价值函数来描述灾民有限理性条件下的效用感知满意度。

假设所有灾区的参考点价值都一样，为V0，且V0＞0，则灾区i的参考点的价值函数为：

其中：表示灾区i的参考点效用，由于各灾区的受灾程度不同，其对参考点的选择也不同，这也体现了个性化的差异，对最优分配方案的选择至关重要。

根据Kahneman 等[7]的研究，灾区i在应急物资分配方案中的价值函数计算公式为：

其中：Ui表示分配方案对灾区i的效用，α 和β 分别表示收益与损失区间的风险偏好水平，λ 表示对损失的规避程度。由于人们在面对相对不确定性的风险和相对确定性的收益时，体现出风险厌恶；而面对相对不确定性的风险和相对确定性的损失时，体现出风险追求。因此，参数取值范围为0＜α, β＜1，λ≥1。

2 应急物资分配模型

2.1 符号说明

I表示灾区的集合，I=｛1,2 , …,n｝，i∈I；J表示中央救灾物资储备库 （以下简称“储备库”） 的集合，J=｛1,2 , …,m｝，j∈J；di表示灾区i的应急物资需求量，可根据受灾程度（如受灾人口数、房屋倒塌数、经济损失数等） 估算得出；sj表示储备库j的应急物资储备量；yij表示储备库j是否对灾区i进行配送，yij∈｛0,1 ｝，是则为1，否则为0；tij表示储备库j到灾区i的配送时间；Ti表示灾区i应急物资的到达时间；f（Ti）表示灾区i的时间感知满意度，且f（Ti）∈［0,1 ］；xij表示储备库j配送到灾区i的应急物资数量，为模型的决策变量；Ri表示灾区i的应急物资实际分配量，即表示灾区i的需求感知满意度，且f（Ri）∈［0,1 ］；ρi表示灾区i的价值系数，与灾区受灾的严重程度有关，严重程度可根据灾区伤亡人数、建筑物倒塌数、震级强度等评估，受灾越严重，价值系数越大。

2.2 效用函数

各灾区的受灾程度不同，导致其对救援时间的感知满意度也不同。对于灾民而言，一般其心里会有一个预期救援时间，也就是阈值，当救援时间小于等于阈值，灾民的满意度为1，当救援时间超过阈值，救援时间越长，满意度越低。时间感知满意度表达式为：

其中，ai为灾区i的时间阈值，当Ti=0 时，表示没有对灾区i进行救援，因此满意度为0；当0＜Ti≤ai时，满意度为1；当Ti＞ai时，满意度随着时间的增大而减小，且时间越大，满意度减小的速度越快。

灾民对应急物资数量的感知满意度可直接用需求满足率表示，其表达式为：

考虑救援时间与应急物资分配数量对灾区的影响，则灾区i的效用函数为：

其中：η 表示时间感知满意度的权重，0≤η≤1。

选择各储备库到灾区i的平均救援时间为时间参考点，同时选择按比例分配的数量为需求参考点，则有：

其中：表示灾区i的时间参考点，表示灾区i的需求参考点（需向上取整），则参考点的效用（即价值函数的参考点）为：

2.3 模型建立

构建考虑灾民有限理性的应急物资分配模型如下：

式（9） 表示最大化所有灾区效用感知满意度的总价值，V Ui（）的表达式见式（2）。式（10） 为Ti的表达式，表示分配给灾区i的应急物资全部到达灾区i所需的时间。式（11） 表示当储备库j对灾区i进行配送时，yij取1，否则取0。式（12） 表示配送给灾区i的应急物资总量不大于其需求量。式（13） 表示储备库应急物资的供应量等于该物资的储备量。式（14） 表示决策变量为非负整数。

3 求解算法设计

设计带精英保留策略的遗传算法对其进行求解，具体步骤如下：

Step1 染色体编码及初始种群产生。根据模型解的特性，采用二维整数编码，即每个染色体X=（x11,x12,…,xnm），其中xi∈Z，i=1,2,…,n×m。矩阵的第i行、第j列对应的元素表示储备库j分配给灾区i的应急物资数量。定义种群规模为popsize，初始种群产生方法如下：

Step1.1 令集合A= ｛1,2,…,n×m｝，p=0；

Step1.2 从A中随机取个数r，令p=r，计算相应的下标，

Step1.3 令 ν=min｛di,sj｝，v=randi（0,ν ），xij=ν，di← （di-xij），sj← （sj-xij），并且A←A/｛p｝，其中函数randi（0,ν ）表示随机生成一个0 到ν 的整数；

Step1.4 检查A是否为空集，若A非空，则返回Step1.2，若A为空集，转入Step1.5；

Step1.5 因为约束条件式（13） 为强约束，为了满足该约束条件，令表示矩阵X中第j列需求满足率最小的行对应的值；

Step1.6 检查生成的染色体是否满足约束条件式（12），不满足则返回Step1.1，满足则结束。

重复以上过程popsize次，得到初始种群X1,X2,…,Xpopsize。

Step2 适应度计算。直接用目标函数值作为适应度。

Step3 选择操作。根据适应度值采用轮盘赌方法进行选择操作，共进行popsize次，得到由popsize个复制染色体组成的新种群。

Step4 交叉操作。采用单点交叉，以交叉概率pc从Step3 产生的新种群中选择参加交叉操作的父代，并将它们随机配对，然后进行“列”交叉，并判断子代是否为可行解，可行则保留，不可行则用Step1 中的方法随机生成一个可行解替换之。

Step5 变异操作。以变异概率pm从Step4 产生的新种群中选择参加变异操作的个体，然后用产生初始染色体的方法生成一个新染色体代替变异的个体，以保证种群的多样性。

Step6 精英保留策略。保留目前为止找到的适应度最高的染色体，并用其替换下一代中适应度最差的个体。

Step7 终止准则。定义最大迭代次数Maxgen，如果当前迭代次数小于Maxgen，则转入Step2，否则算法结束，输出结果。

4 案例分析

4.1 案例背景

以2013 年四川芦山地震应急救援为例，该地震震级为7.0 级，震源深度13 公里，属于浅源地震，因此房屋倒塌非常严重，灾区急需帐篷。民政部从灾区周边6 个中央救灾物资储备库向灾区调运首批应急物资5 万顶帐篷，其中成都、昆明、西安、兰州储备库各调运1 万顶，武汉、长沙储备库各调运0.5 万顶，各储备库到各灾区的时间见表1。

心理感知时间阈值ai与灾区的受灾程度有关，芦山县、天全县和宝兴县受灾较为严重，设置其阈值为12h；雨城区、名山区、荥经县和邛崃市受灾程度一般，设置其阈值为24h。灾区需求根据倒塌房屋数估算得出（见表2），根据式（3） 至式（8）可计算出各灾区的时间参考点、需求参考点及参考点效用，计算结果见表2。由Tversky 等[9]的分析可知，α=β=0.88，λ=2.25。设置时间感知满意度权重η=0.5，参考点价值V0=0.5。根据受灾的严重程度，设置各灾区价值系数为此外，平均需求满足率

4.2 计算结果分析

根据算法设计，采用MATLAB 编程，在Intel Core i7 @ 2.60GHz CPU，8.00GB 的计算机上对案例进行计算。经过多次测试，确定最佳参数为：种群规模popsize=500、最大迭代次数Maxgen=400、交叉概率pc=0.9、变异概率pm=0.1。程序运行19.63s 计算出问题的近似最优解（见表3），目标函数最优值为9.829。带精英保留策略的遗传算法性能跟踪见图1，可见随着迭代次数的增加，种群的平均适应度逐渐提高，目标函数最优值也逐渐提高并收敛。

由表3 可知，对于芦山县和宝兴县，实际救援时间都小于时间阈值，但需求满足率都低于平均需求满足率，这是由于只有成都储备库能在时间阈值内到达这两个灾区，而成都储备库的帐篷供应量有限；对于天全县、名山区和荥经县，虽然没能在时间阈值内到达灾区，但是需求满足率都大于平均需求满足率，需求感知满意度弥补了时间感知满意度的损失。对比表3 的实际效用和表2 的参考点效用，可以发现实际效用都大于参考点效用，可见这样的分配方案可使灾民感知满意度维持在一定程度，从而避免灾民的心理恐慌及非理性行为的发生。

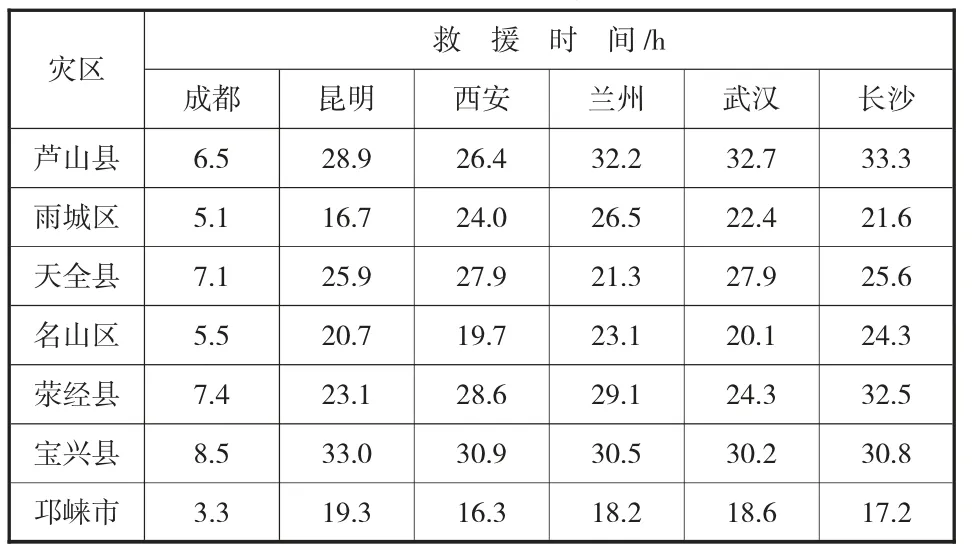
表1 储备库到灾区的救援时间

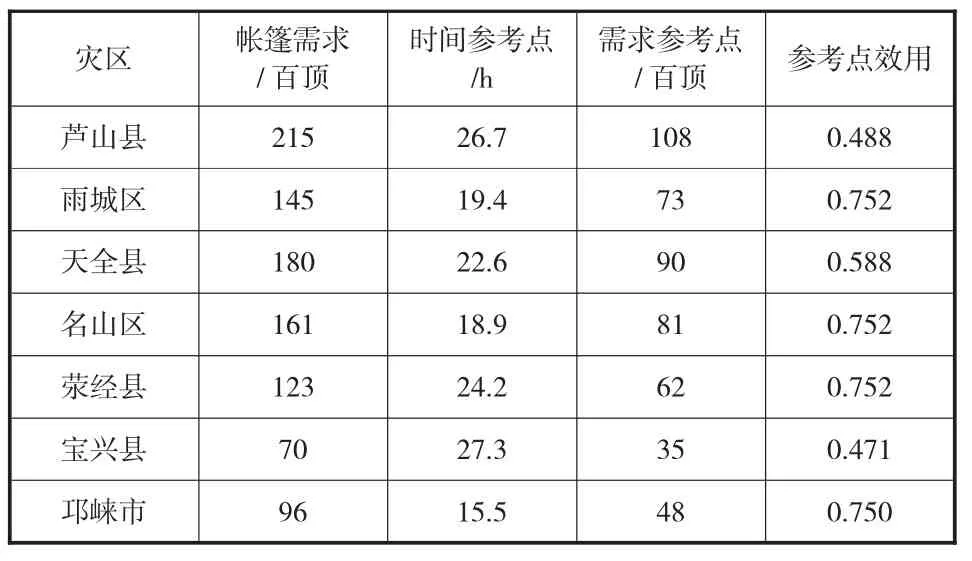
表2 案例相关参数表

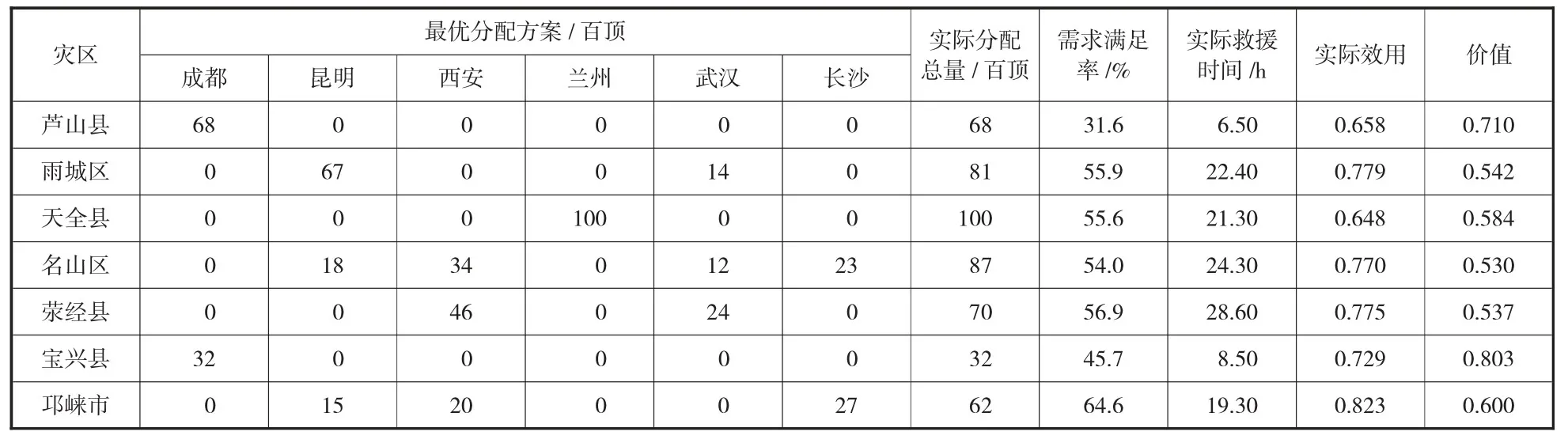
表3 总价值最大的最优分配方案

案例分析说明本研究所构建的模型能较好地模拟灾民的有限理性，根据算法求解得到的应急物资分配方案，可使灾民感知满意度维持在一定程度，从而缓解灾民的心理恐慌。

5 结束语

本文以各储备库到灾区的平均救援时间为时间参考点，以按比例分配的应急物资数量为需求参考点，使应急物资的分配更加具有公平性；在此基础上，构建考虑灾民时间感知满意度和需求感知满意度的效用函数，用价值函数表示灾区的效用感知满意度，不仅使满意度的衡量更符合人的实际心理，还体现了灾民有限理性对应急救援决策的影响。

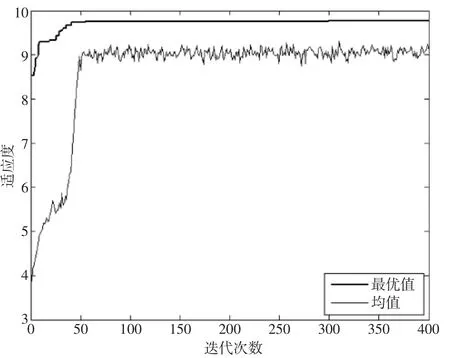
图1 带精英保留策略的遗传算法性能跟踪图