高校快递包装回收模式的经济性比较及选择

张晶蓉，吴雅婷，张彦雨，刘青松 （郑州大学，河南郑州450000）

ZHANG Jingrong, WU Yating, ZHANG Yanyu, LIU Qingsong (Zhengzhou University, Zhengzhou 450000, China)

0 引 言

近年来，随着电子商务的快速发展，网络购物异军突起，快递行业日益繁荣。根据中国快递发展指数报告显示，2018 年我国快递业务量总计507.1 亿件；2019 年同比增长25.3%，连续两年增量规模超过100 亿件。快递行业的高速发展伴随着产生数以万计的快递包装废弃物，不仅浪费资源，而且污染环境。快递包装回收再利用可以节约原材料，降低生产成本，同时减少对环境的损害。

大学生作为网购的主力军，推动了高校快递业务量激增，使大学校园成为快递包装废弃物的主要聚集场所之一。然而，由于回收成本高、缺乏回收渠道、回收体系不完善等问题，快递包装回收再利用率低下，造成了严重的资源浪费和环境污染。因此，提供有效便捷的回收渠道，选择高效率低成本的回收模式，对开展高校快递包装回收工作至关重要。

近几年快递包装回收模式相关研究备受关注。乐雄平[1]针对电商企业的包装物进行研究，提出了自营物流回收模式，通过减少回收的中间环节来提高资源利用率。李正军[2]基于网络众包提出一种新型的快递包装回收模式，通过引入数字化的智慧管理系统创新管理模式，用以提高快递包装回收效率。吴亚霄[3]综合考虑经济因素、管理因素和社会因素建立回收模式选择的评价指标模型。鲁芳[4]从消费者环保意识出发，比较分析第三方回收商模式和电商物流企业回收模式的最优利润。

在高校快递包装回收方面，张晶蓉[5]基于现有校园快递服务点，研究高校快递纸箱回收再利用层级网络中物流节点的选址布局。杨传厚[6]总结了校园快递包装回收的现状和问题，构建校园快递包装回收系统，优化回收流程。汪梓懿[7]运用智慧物流理念对高校快递包装回收流程进行再造和优化，以提高高校快递包装回收效率。王岩松[8]提出一种由回收站、快递收发站、微信平台组成的新型快包装回收模式。娄婷婷[9]运用层次分析法，根据回收意识和回收成本构建评价指标体系，分析比较三种快递包装回收模式。

综上所述，在高校快递包装回收方面已有不少研究成果，但在高校快递包装回收模式经济性的定量分析比较以及模式选择方面还有不足。鉴于此，本文以高校为背景建立快递包装回收的逆向供应链模型，并从不同的回收负责主体角度提出了三种回收模式，基于考虑快递点回收模式下废旧包装的重复使用建立数学模型，运用逆向归纳法求解，得到不同回收模式在均衡条件下的各回收参与方的最优利润和最优回收量，据此分析比较三种回收模式的经济性，并提出回收模式选择建议。

1 模型描述

1.1 问题描述

本文研究的逆向回收系统由快递包装生产商、高校快递服务商和高校组成，回收过程中，生产商是回收价格制定的领导者，快递服务商和高校是跟随者。基于快递包装回收模式的研究，本文结合高校背景提出包装生产商回收模式、快递点回收模式和学校回收模式。

在一定条件下，回收的快递包装经过简单的处理可进行重复使用，或者作为原材料进行再制造。循环经济理论3R 原则的优先顺序为减量化、再使用、再循环利用[10]，因此本文在研究废旧快递包装回收再利用时优先考虑重复使用。高校快递服务商作为快递包装的直接使用者，可利用其现有的业务重复使用回收的快递包装。因此，本文在快递点回收模式下优先考虑废旧包装的重复使用，包装生产商回收模式和学校回收模式只考虑将废旧包装物作为原材料进行再制造，并探讨重复使用比率λ 对校园快递包装回收模式选择的影响。三种回收模式分别如图1 中（a）、（b）、（c） 所示。

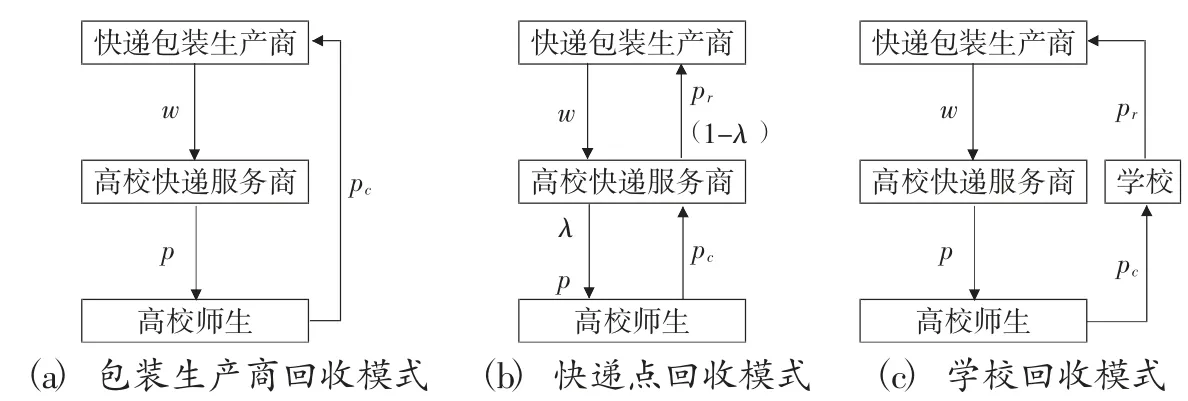
图1 回收模式的决策模型

1.2 模型符号

w：批发价格，快递包装生产商给予快递包装使用企业的价格；

p：快递包装物的单位零售价格，高校快递服务商向消费者收取的费用；

pc：直接回收价格，从消费者手中回收单位快递包装物所支付的费用；

pr：包装生产商从快递服务商或学校手中回收快递包装支付的转让价格；

CLτ2：根据Savaskan[11]在文献中的表示，CLτ2为固定投资成本，τ 是负责回收的主体决定投入的回收努力程度，CL是大于零的常数；

k：代表高校师生的环保意识，即未建立回收系统时，高校师生自发无偿回收废旧快递包装的数量，环保意识越强，k越大，且k≥0；

Q：废旧快递包装回收量，由回收价格pc、回收努力程度τ 决定；

θ：再制造生产率，即以回收的快递包装物为原材料进行再制造，能够制成新包装的数量与进行再制造的废旧快递包装数量的比值（0＜θ＜ 1 ）；

λ：重复使用比率，回收的快递包装物中经过简单处理可被重复使用的比例（0＜λ＜ 1 ）；

cd：以回收的废旧资源生产新包装的单位成本，通常情况下cd小于利用原材料生产新包装的单位成本；

cm：快递服务商负责回收工作时，将回收的产品进行简单分类处理，挑选出可重复使用包装物的成本；

1.3 模型假设

假设1：快递包装回收量的大小由回收价格和回收努力程度两个因素决定，即回收量的函数为Q（pc,τ）=k+apc+bτ（a＞0 ,b＞0 ）。其中a是回收价格系数，表示高校师生对回收价格的供给弹性；b为回收努力程度系数，表示τ 对回收量起促进作用；

假设2：针对生产商而言，回收Q单位的废旧包装物可再制造得到θQ的再生新包装物，比值θ 受回收包装物质量的影响；

假设3：假设可重复使用的快递包装、再制造获得的再生包装和新包装在质量、性能、价格上无差异；

假设4：假设参与回收的主体是理性经济人，即参与快递包装回收活动都能从中获得利润，利用废旧快递包装进行再制造的生产成本低于新包装的生产成本；

假设5：在逆向回收过程中，信息完全公开，生产商对回收市场有足够的控制能力，是Stackelberg 领导者，且各回收参与方均以利润最大化为目标；

假设6：回收的快递包装经过简单分类即可重复使用的比率为λ，为简化研究，将其定为常数，后期可研究λ 的大小对回收模式选择的影响。由于经济人假设，对于高校快递服务商而言，优先选择重复使用的条件是通过重复使用获得的利润大于再制造所获得的利润，需满足p-cm/λ＞θw-cd，则 1＞λ＞cm/（p-θw+cd）＞0。

2 模型建立及求解

2.1 包装生产商回收模式

包装生产商回收模式中，由生产商确定回收价格和回收努力程度。生产商以回收价格pc从高校师生处回收废旧快递包装，回收量为Q，经再制造获得全新的包装为θQ。此模式下包装生产商的利润为：

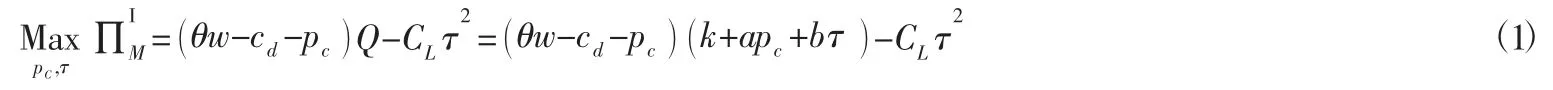
对公式（1） 关于pc和τ 求一阶偏导得：

求包装生产商利润的二阶导数，得到Hessian 矩阵如下：

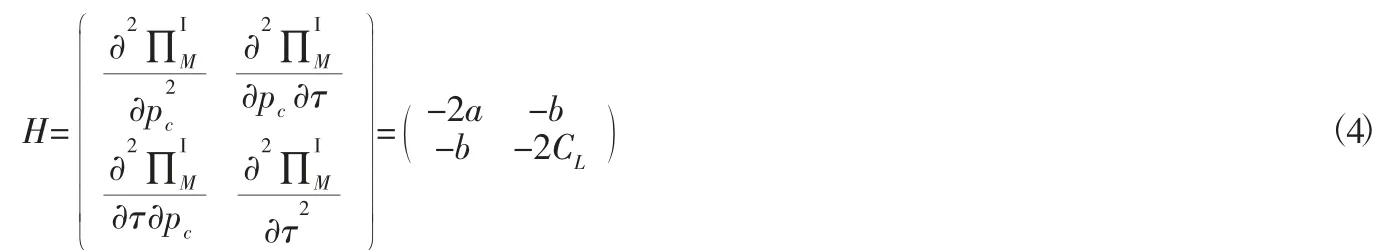
将和τI*带入回收量函数Q和包装生产商的利润函数中，可得：

2.2 快递点回收模式

在快递点回收模式中，首先高校快递服务商确定回收价格pc和回收努力程度τ，然后包装生产商决定转让价格pr。快递服务商以回收价格pc收集废旧快递包装，回收量为Q。经过简单分类，λQ的快递包装留下重复使用； （λ- 1）Q的废旧包装转让给包装生产商进行再制造，得到θ （λ- 1）Q的全新快递包装。

此模式下高校快递服务商的利润为：

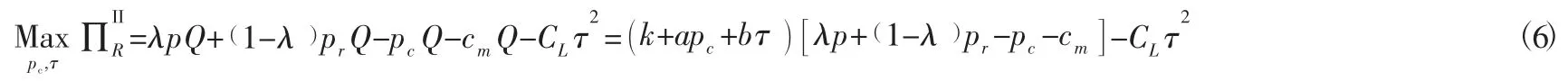
包装生产商的利润为：

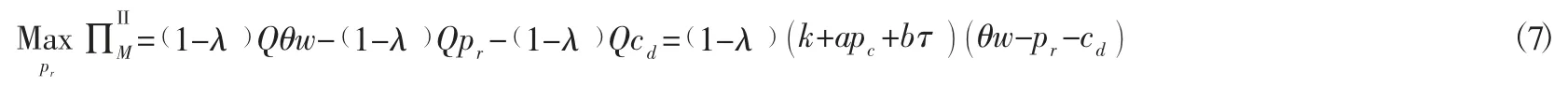
根据逆向归纳法，利用高校快递服务商的利润对pc和τ 求一阶偏导，令联立求解方程组得：

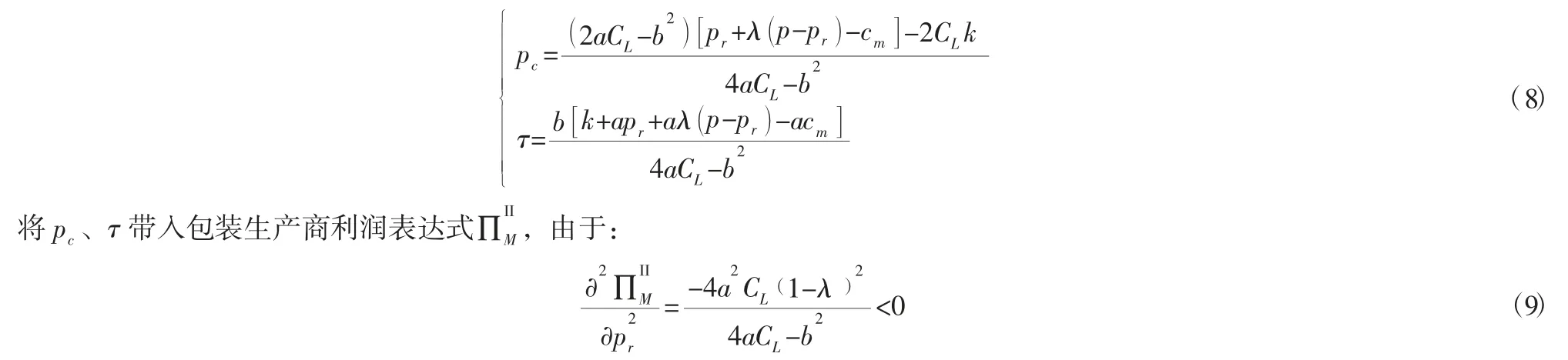
所以包装生产商利润的决策有唯一最大值，对pr求一阶导数令其为零，求得快递点回收模式下最优转让价格为：

将带入pc、τ 求得最优回收价格和回收努力程度τII*。

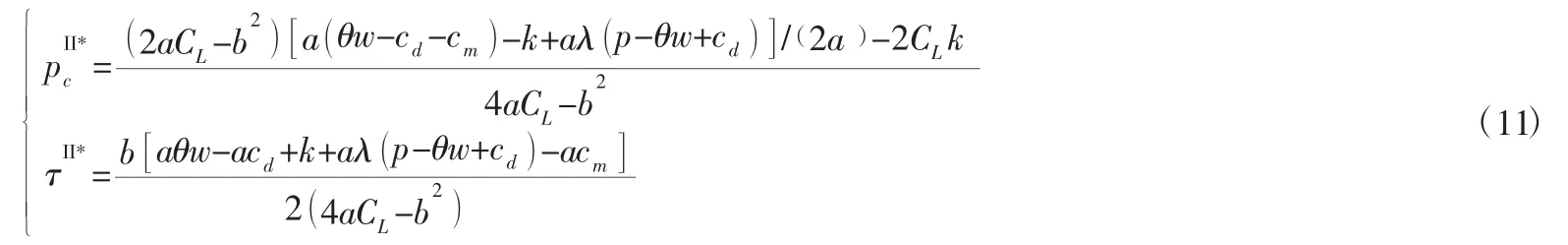
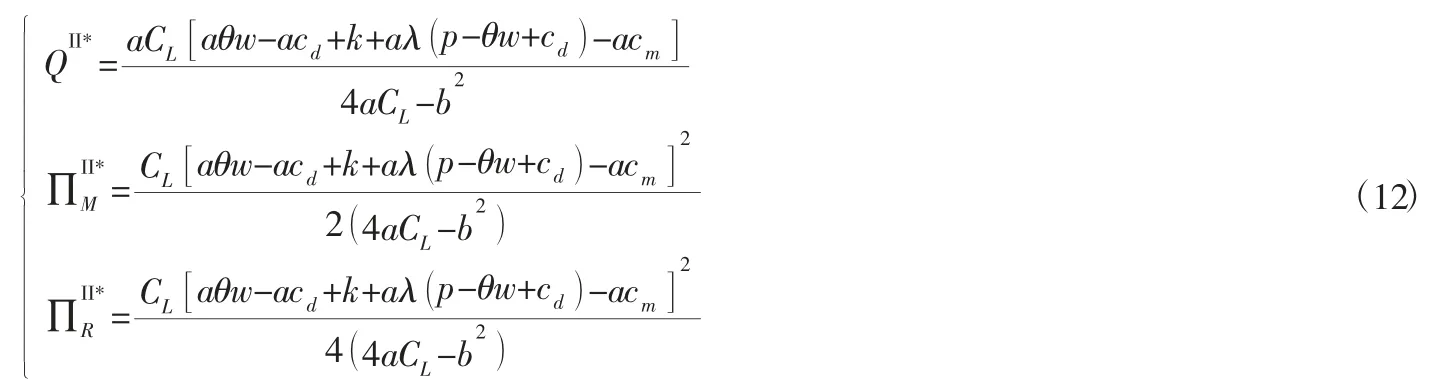
2.3 学校回收模式

在学校回收模式中，高校负责开展回收工作，决定回收价格pc和回收努力程度τ，生产商确定转让价格pr。其中高校的利润为：

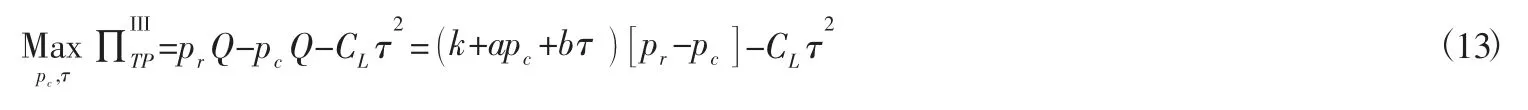
包装生产商的利润为：

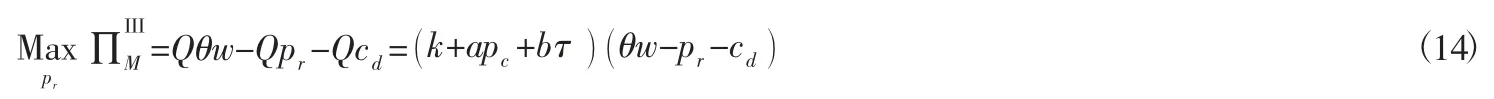
同理快递点回收模式的计算过程，利用逆向归纳法可求得：

2.4 三种回收模式的对比分析

基于不同回收模式的计算结果，为了更直观地比较三种模式的优劣，令X=aθw-acd+k（X＞ 0 ）、Y=aλ（p-θw+cd）-acm（Y＞ 0 ），A=4aCL-b2＞0 进行简化，三种模式下的回收数量、最优利润值如表1 所示：

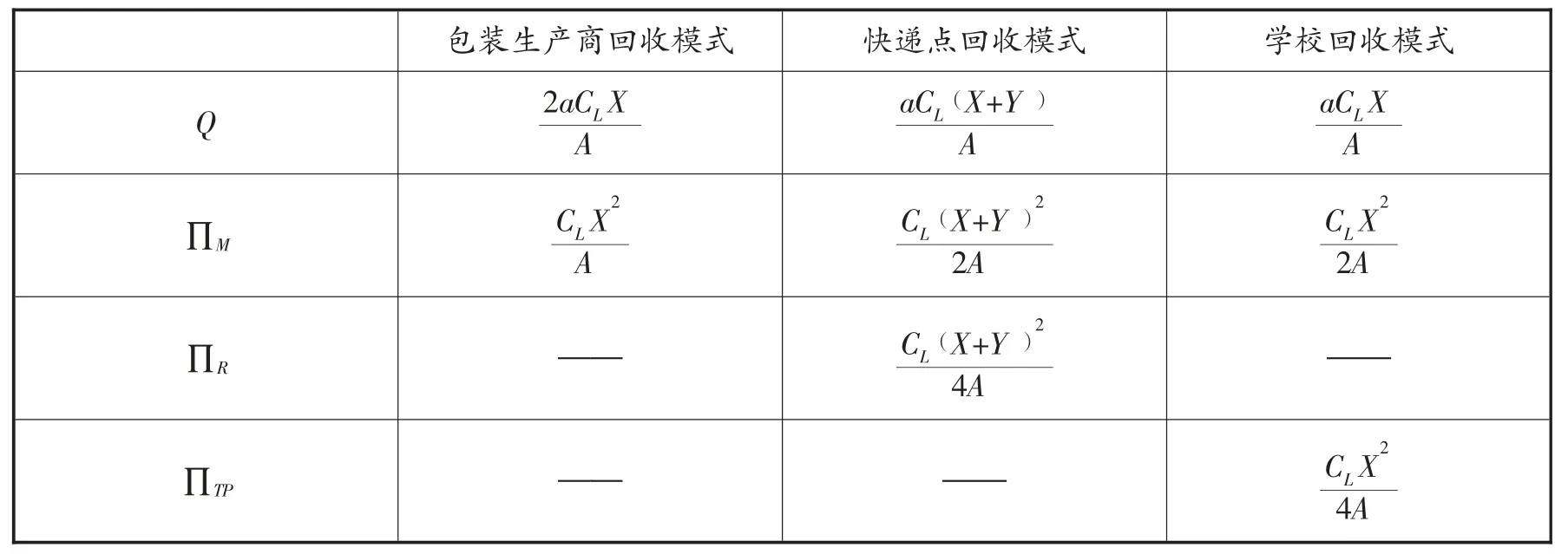
表1 不同回收模式下各个参数的最优值

由表1 可直接得出以下推论：

推论1：当包装生产商选择将快递包装回收工作外包给快递服务商或者第三方（高校） 时，生产商与快递服务商、高校的利润分配最优比值为2∶1。因为：

推论2：无论在何种回收模式下，再制造生产率越大，越有利于开展回收工作，因为回收数量、回收参与方的利润都是关于θ 的增函数。其中θ 的大小与回收的快递包装的质量、再制造处理技术的高低有关。

推论3：当所有参数保持一致时，以下不等式一定成立：

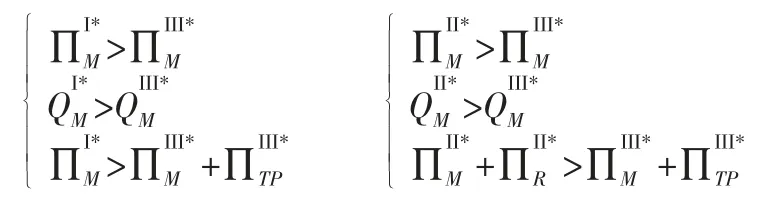
推论3 说明从经济性角度出发考虑利润和回收量，包装生产商回收模式和快递点回收模式都优于学校回收模式。从表1 中可看出，当不考虑快递包装的重复使用时，快递点回收模式和学校回收模式的回收效果相同，由于本文假定废旧快递包装通过重复使用获得的效益高于再制造，所以优先考虑重复使用的快递点回收模式在经济性方面优于学校回收模式。

3 回收模式的经济性比较与选择

下面分别从生产商获得的利润和回收量角度来比较三种回收模式的经济性优劣，对不同回收模式进行分析选择，并针对模型中的参数重复使用比率λ 进行分析。

3.1 基于生产商利润的回收模式选择

本节从包装生产商的角度出发，分析比较不同回收模式下包装生产商的最优利润。由推论3 可知，所以以下关键点在于的比较。当不同回收模式的其它参数相同时，生产商最优利润的大小相互关系取决于λ、p、w等参数的大小。并有关系式如下：

推论4：

由推论4 可知，当重复使用废旧快递包装所带来的收益与再制造所带来的收益的相关比值较小时，应选择包装生产商回收模式，虽然重复使用快递包装会使快递点回收模式性能更优，但不足以使其超越包装生产商回收模式。当上述比值较大时，快递点回收模式在重复使用比率较大的条件下性能更优，重复使用比率较小时应选择包装生产商回收模式。

算例分析：

为了更直观清楚地说明推论4，研究重复使用比率对回收模式选择的影响，可通过数值分析作进一步阐述。将重复使用比率λ 设置为未知数，其他参数假设为定值，且参数之间的相互关系满足上文所有假设。

假设k=20，a=40，b=10，CL=30，w=2，cm=0.2，θ=0.9，cd=0.5，p=2.2，根据假设 6 可知 λ 的取值范围为 0.22＜λ＜1。将上述参数分别带入三种回收模式下的生产商的最优利润中，随着参数的改变，三者的大小关系如图2 所示。

由图2 中可知，在其他参数确定时，包装生产商回收模式和学校回收模式下的生产商的最优利润是确定的，且恒成立。随着重复使用比率λ 增大，虽然快递点回收模式下生产商的利润也在增大，但其始终小于包装生产商回收模式下生产商的利润，即上述结论说明，当重复使用废旧快递包装所带来的利润相对较小时，由生产商自行负责快递包装回收的经济效益更佳。

参数k、a、b、CL，w、cm与上文保持一致，假设 θ=0.7，cd=0.6，p=2.4，此时 λ 满足 0.125＜λ＜1。随着 λ 的改变，三者的大小关系如图3 所示。

3.2 基于回收量的回收模式选择

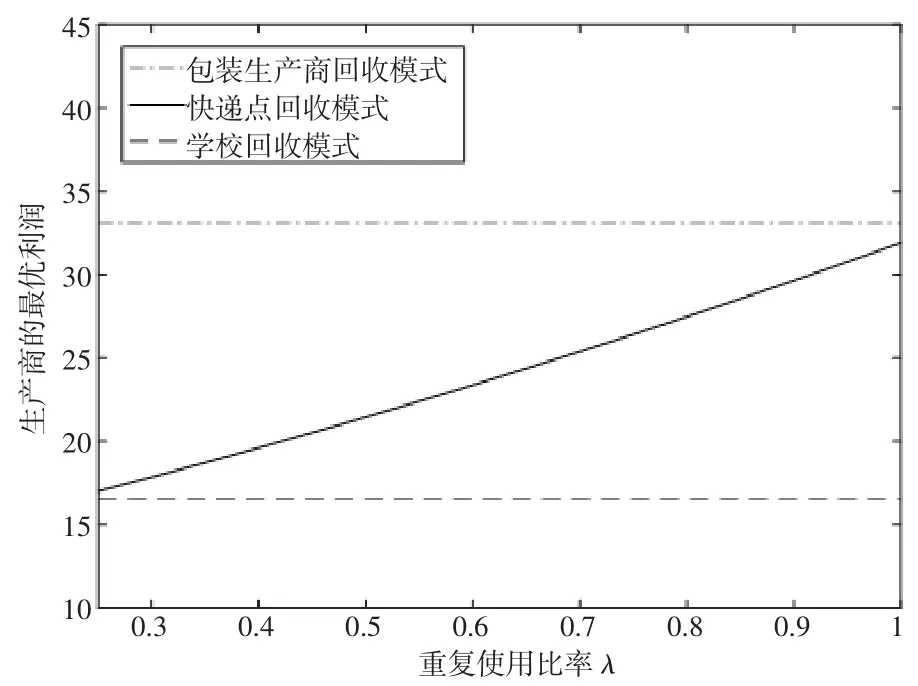
图2 三种回收模式下包装生产商的利润

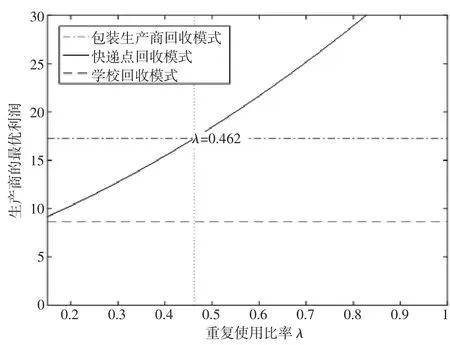
图3 三种回收模式下包装生产商的利润

本节讨论快递包装回收量对回收模式选择的影响。废旧快递包装的回收量越多，越容易形成规模效益，同时对环境的影响越小，进而形成良好的经济性效益。当其它参数相同时，有以下关系式成立：

推论5：

推论5 表明基于回收量的回收模式选择和基于生产商利润的回收模式选择的结果保持一致。当重复再利用的利润够大且重复使用比率较大时，应选择快递点回收模式，否则应选择包装生产商回收模式。

算例分析：

同理为了更直观地表述推论5，采用数值分析法，将λ 设为未知数，k、a、b、CL，w、cm与3.1 节中参数的取值保持一致，且参数之间的相互关系满足上文所有假设。

令θ=0.7，cd=0.5，p=2.4，此时λ 的取值范围为0.133＜λ＜1。将上述参数带入不同回收模式下的最优回收量中，随着参数λ的改变，的大小关系如图4 所示。

由图4 可知，当重复使用回收的快递包装所带来的利润较小时，虽然λ 对快递点回收模式下的回收工作有促进作用，但其始终小于包装生产商回收模式下的最优回收量。所以，从回收数量出发，应选择包装生产商回收模式。

假设θ=0.7，cd=0.8，p=3，其他参数同上，λ 的取值范围为0.083＜λ＜1。此时与λ 的关系如图5 所示。

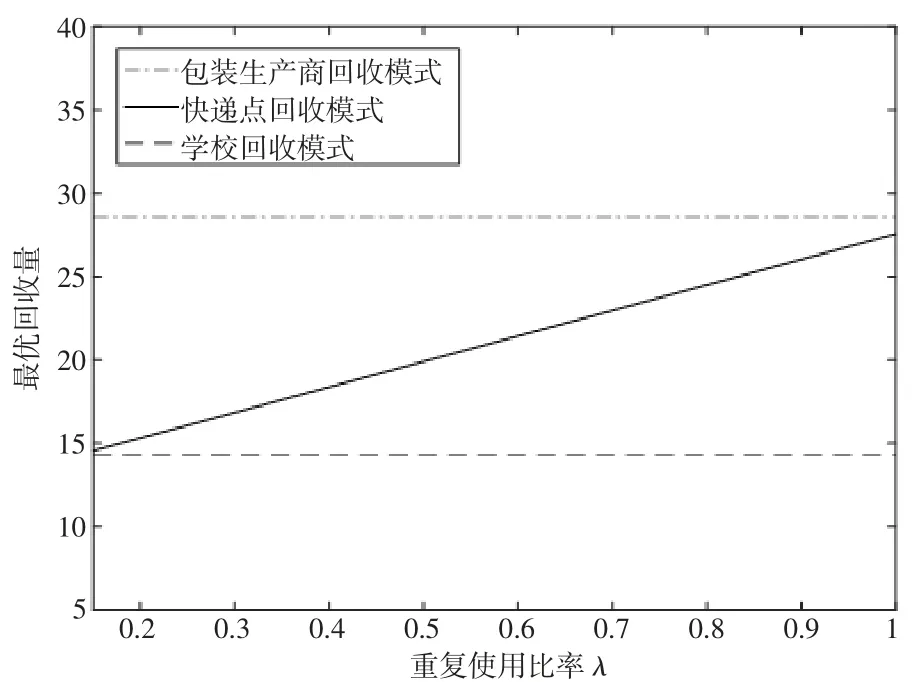
图4 三种回收模式下的最优回收量

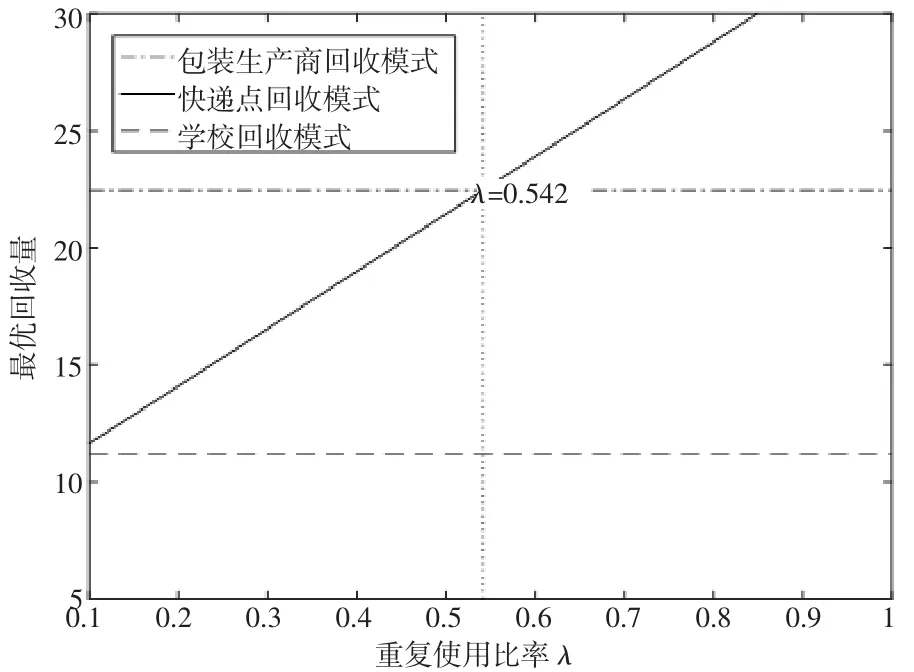
图5 三种回收模式下的最优回收量

同理，通过图5 可以看出，基于上述参数假设，当0.083＜λ＜0.542 时，应选择包装生产商回收模式使得效益最大化，当0.542＜λ＜1 时，应选择快递点回收模式。

4 结束语

本文以高校内的快递包装为研究对象，探讨了快递包装回收模式的选择问题，为高校推行快递包装回收提供一定参考。本文提出了三种高校快递包装回收模式，并根据回收过程中各成员获得的利润建立数学模型，运用逆向归纳法求得不同回收模式下的最优回收量和利润值，进行经济性对比分析，并通过具体的算例来表现三种回收模式的直观对比结果。主要结论有：（1）当重复使用快递包装所带来的收益较小时，由包装生产商负责回收所带来的经济性效益更佳；（2） 当重复使用的收益相比于再制造的收益较大，且重复使用比率高于一定值时，选择快递点回收模式效果更佳。

本文假设不同回收模式的固定投资成本相同，而实际上快递服务商可利用其正向物流设施减少回收设施建设的投资成本。因此，在接下来的研究中要综合考虑不同回收模式固定投资成本的差异，得出更加符合实际的结论。