数学知识视觉化呈现原理、方法与实践研究

尚晓青 许佳 陈明璋

[摘   要] 在我国学生数学理解水平仍逊于国际平均水平的状态下，促进学生的数学理解仍然是深化数学教学改革的重要议题。借助于信息技术，数学知识的视觉化呈现为促进学生的数学理解提供了突破口，在以知识结构化与呈现区块化融合、知识呈现步骤化与口语简化引导融合、情境与数学信息呈现融合、视觉刺激标识与建立信息关联融合为基本方法的指引下，视觉化呈现方式能通过视觉强化吸引学生注意力、调节学生的认知负荷，为学生理解数学搭建阶梯。研究以视觉化呈现的教学设计为自变量，开展了“初步认识分数”单元的整体设计和准实验研究，研究结果证实，知识视觉化呈现能够促进学生理解数学，尤其对于中等及以下学生的学习效果具有显著影响，能够为内在认知负荷较高的教学难点搭建理解的脚手架，能够在不同程度上提高学生的识记、领会以及分析能力。

[关键词] 知识呈现; 视觉化呈现; 教学设计; 认知负荷

[中图分类号] G434            [文献标志码] A

[作者简介] 尚晓青（1979—），女，陕西蒲城人。副教授，博士，主要从事教师教育、数学学科教学论研究。E-mail：shangf9@snnu.edu.cn。

一、问题的提出

数学作为培养公民素质的基础课程，为学生未来的工作、学习和生活奠定重要的基础[1]。然而在基础教育阶段，我国学生对数学思想方法、数学思维以及数学精神的领悟仍逊于国际平均水平[2]，由此可见，促进学生对数学本质的理解仍然是深化数学教学改革的重要议题。事实上，学生的数学理解水平与数学本身特性有关，更与教师的教学相关，特别与教师在课堂中提供的知识以及引导方式有密不可分的关系。研究表明，學生学习跟他们工作记忆加工容量相关[3]，受到他们的视空和语义信息加工能力的影响[4]。在信息技术时代，如何融合数学、教学以及技术特征于一体，在课堂中有效地引导学生排解视觉加工障碍，形成有意义的语义链接，提高工作记忆、加工效率，就成为突破数学本质理解的关键。本研究旨在通过数学知识的视觉化呈现设计，借助技术的视觉化功效，凸显数学知识要点及其结构关系，引导学生有效地进行知识学习的视觉加工和语义链接，从而达到对数学本质的理解。

二、数学知识视觉化呈现原理

知识的视觉化呈现是基于认知负荷、多媒体学习以及注意力引导理论而提出的教学设计概念，其核心是依据多媒体学习原理，借助多媒体应用，降低知识表征中所产生的外在认知负荷，通过视觉上凸显知识的结构关系，转化知识本身的内在认知负荷，进而实现注意力引导和知识建构的教学目标。

（一）结构化知识呈现有利于学生建构良好的知识结构

知识结构是认知结构的反映，是获得新经验或知识、扩大认知结构的基础[5]。学生的学习是一个知识结构的不断形成与发展过程。在教学中，结构化的知识经验可以减少工作记忆中的信息组块数量，可以有效降低学生学习中的认知负荷[6]。利用结构化的知识组织能够为学生建立起已有知识与所学知识之间的有效连接，引导学生开展知识结构的建构活动，帮助学生厘清知识之间的脉络关系，强化认知，促进知识的记忆和提取。在数学教学中，结构化的学习材料能够激发高层次数学思维[7]，通过凸显数学知识本身所包含的基本概念、法则或原理及其之间的结构关系，让内在认知负荷比较高的知识组织元素、发展逻辑、结构层次变得可视化、形象化，有利于引导学生通过知识建构过程形成良好的数学知识结构，发展数学思维。

（二）均衡认知负荷的多媒体呈现设计能提高工作记忆加工效率，有利于学生的意义建构

认知负荷理论认为，在认知结构的形成中，工作记忆容量的有限性和长期记忆的无限性会有许多干扰因素。例如，不恰当的教学设计就会形成外在认知负荷，会导致学习者没有多余的认知资源来建立知识之间的联系而形成认知结构[8]。均衡认知负荷的教学设计可以降低学生在认知过程中的心理干扰，引导学生形成有意义的知识建构[9]。Sweller John提出的十四个认知负荷效应[10]、Mayer Rechard和他的团队根据视听觉通道的信息处理特征以及多媒体技术特征提出的多媒体技术应用的十项原则[11]，都为开展均衡认知负荷的教学设计提供了重要参照。

均衡认知负荷的教学设计主要从降低外在认知负荷、优化内在负荷、增加相关认知负荷三个层面来实现[10]，这三个层面为意义建构的发生与深化提供了条件。一是通过技术呈现方式和组织形式的设计，减少非知识本质的外在因素干扰，降低学习过程的外在负荷，为学生开展核心知识的意义建构排除干扰;二是通过分割、区块化、群化等策略，凸显知识本质结构及知识元素之间的关系，从视觉上解构数学知识发生的逻辑，有利于转化数学知识的内在认知负荷[12]，引导学生发现数学知识的内在认知逻辑，推动学生开展有意义的建构活动;三是通过多元表征、口语引导以及样例学习等，变换知识情境，增加知识之间的广泛联系，增加相关认知负荷[13]，让学有余力的学生在意义建构达成之后，实现对意义建构过程的深化。

（三）建立视觉化信息关联以强化注意力引导，实现认知负荷的均衡化

注意力机制存在的基本假设是人的心理资源是有限的，无法同时处理过多事项，知觉的对象和背景在视觉上差别越大，越能被知觉选择注意到，活动的对象越容易进入知觉[14]。在知识呈现的过程中，教师可以通过多媒体技术增加标识符、加强颜色明暗对比、添加动态要素等操作来加强知识结构的外在表征刺激，有效地把学生的注意力吸引到知识结构的建构上[12]。

建立视觉化信息关联可以强化元素交互关系，一方面可有效凸显内在认知负荷的结构，凸显知识之间的关系、表达知识建构中的逻辑，在促进有意义建构学习发生的同时，变相地降低内在认知负荷。另一方面通过元素互动性，可以有力地增加外在负荷和相关负荷之间的互动，达到降低外在认知负荷、为相关认知负荷腾出认知空间的目的[15]。从视觉角度建立信息关联，强化重要信息以及信息之间的视觉刺激，通过注意力引导，能够有效地为认知搜索和链接节约时间，进而达到降低外在认知负荷的目的。因此，建立视觉化信息关联是促进认知协调的重要手段。

五、研究结果与分析

（一）实验后两班学生学习成绩的对比差异

研究中，分别在“分一分（二）”“吃西瓜”“比大小”三节课以及单元教学之后进行了学习成绩测试。

在“分一分（二）”（T=2.795，p=0.006）、“吃西瓜”（T=2.011，p=0.040）、“单元测试”（T=2.846，p=0.007）中，实验班的成绩显著高于对照班;而在 “比大小”（T=1.406，p=0.299）这节课的测试中，两个班没有显著差异。从标准差值来看，对照班学生成绩标准差（6.76，5.29，3.04，14.55）始终要高于实验班（2.84， 3.25，2.07，8.68）。在分数单元测试中，通过对識记、领会、应用、分析四类得分分别进行统计并分析，发现在识记（T=2.607，p=0.012）、领会（T=2.254，p=0.027）、分析（T=2.719，p=0.008）三类题目中，实验班得分显著高于对照班，而在应用类题目中，两班无显著差异。因此，研究假设的验证结果可以描述为：知识视觉化呈现对学生的学习具有一定的积极作用。

（二）知识视觉化呈现有利于处理内在认知负荷度比较高的内容

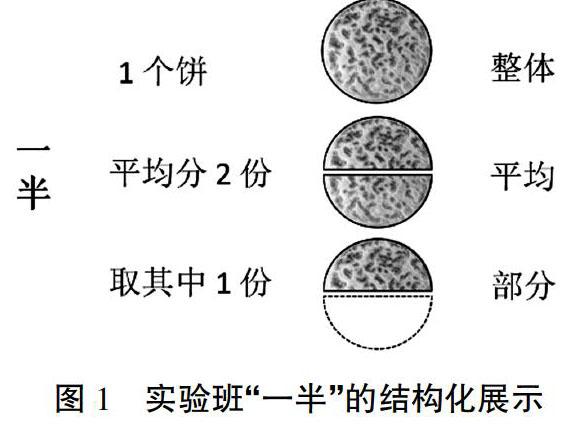
教学内容本身对学生认知需求的差异性，导致课堂测试结果也表现出不同的差异性，从这些差异来看，视觉化呈现设计有利于处理内在认知负荷度比较高的内容。在三次新课学习中，仅“比大小”这节测试结果显示两个班无显著差异，原因在于本节所学新知对学生来说内在认知负荷较低，学生能够借助“整数比大小”的认知策略与经验开展分数比较，容易理解分数比较大小的规律。相比较之下，“分数概念认识”和“分数运算”对于学生的认知需求相对较高，由于分数概念的抽象性，分数概念启蒙教学有效性是世界性问题[17]，问题情境虚化、情境与数学断层等都影响着学生分数概念的形成。在分数概念的初步认识中，学生原有的认知结构已经不能处理现有所面对的问题，会出现认知冲突，需要有新的认知策略对问题进行理解。视觉化呈现中用生活情境让学生认识分数的意义，从生活语言、文字语言逐步过渡到分数的数学语言，建立起情境、生活与数学之间的联结，为学生搭建由已知通向未知的桥梁，提供一个建构性学习的脚手架。在“同分母分数加法”的学习中，学生往往会移植整数加法，从而出现“分母相加、分子相加”的问题;“分母不变”这个法则对于他们来讲比较难理解，而在视觉化呈现设计中，教师通过情境、图片与分数的结构化展示，强调两个相加分数来自于一个整体（情境或图片）这个细节，暗示学生“相加之后的那个份数是不发生变化的”，有效地排除了外在认知负荷的干扰，且把学生的注意力直接引向对内在概念的建构与分析上，让学生经历由形象到抽象的认知过程，有效地避免了由于内在认知负荷高而产生学习焦虑情绪。

（三）知识视觉化呈现能够在一定程度上突破教学难度

知识视觉化呈现对于中等水平及其以下学生学习的有效性引导更为明显。一方面，从两次测试的标准差变化中，可以判断出对照班学生感知的题目难度比较大，在初始测试中，对照班的标准差（9.88）与实验班标准差（8.62）相当;而在分数单元最后测试中，对照班的标准差（14.55）比实验班的标准差（8.68）高了5.87，数据显示，对照班成绩离散程度在单元测试中变大，说明和实验班相比较，对照班学生感知的题目难度偏大。另一方面，通过对学生前后两次成绩的分段统计，对照班低分段人数在实验后有所增加。对照班有更多的学生进入了比实验前低的分数区域，而高分区尤其是90分以上的学生人数未有显著变化，相对实验前，60～70分和50～60分这两个区间的人数增多，80～90分之间的人数减少。实验班实验前后的标准差变化不大，分数集中，其低分段50～60分、60～70分的人数比对照班人数少，说明实验班学生感知的“单元测试”难度整体小于对照班。两方面的数据说明，实验设计能够在一定程度上解决学生学习的难点。数学学习的主要难度来源于它的抽象性，抽象问题形象化以及概念形成过程的体验都是促进学生数学理解的重要突破点。在知识视觉化教学设计中，把抽象的概念进行结构解析、并加以视觉步骤引导，能够降低教学时学生的工作记忆容量，帮助学生进行知识的提取和理解，这些恰恰是学习困难学生的需求， 而学优生对知识的提取与分析、工作记忆的容量以及处理都存在优势[18]，知识呈现方式的改变对他们影响不大，他们对于这种降低工作记忆容量的教学设计需求程度相对比较低。综上可知，知识视觉化呈现设计对于中等及以下学生的学习具有显著促进作用。

（四）知识视觉化呈现有利于学生识记和分析问题能力的形成

视觉化呈现中通过色彩、情境等视觉刺激，强化数学符号表象和数学情境活动之间的链接，为学生提供有意义的活动经验，有利于刺激大脑形成深刻的印象，帮助学生形成良好的长时记忆，识记部分测试已经显示出两个班具有显著差异性。单元测试的识记内容主要考察的是学生长时记忆的有效性，长时记忆存储的有效性绝大部分来源于短时记忆存储的精致性加工[19];而在短时记忆信息登录中，视觉强化刺激相比语言刺激更有利于文字和符号加工[19]。因此，结构化知识呈现有利于引导学生在工作记忆的有限条件下，实现对知识的精加工和知识图式的有效建构，为后续知识的存储和提取奠定基础，促进长时记忆的形成。

视觉化呈现有利于提高学生的分析能力。分析是一种把材料分成各个组成部分，并弄清各部分之间的相互关系及构成方式的能力[20]。知识区块化和结构化能够为分析提供基础和目标导向，数学知识之间关系的连通性和条理化呈现是保障学生思维的流畅性和逻辑性、促进数学问题分析目标达成的重要手段。视觉化呈现在引导学生分析已知到未知之间的联系时，通过情境与知识、生活与数学、数学与数学之间的多重关系链接，表达了分析的方向，在完成数学概念的泛化与分化中，帮助学生形成概念网络并掌握其建构方法，为学生分析型思维的培养提供了条件。

实验结果显示，两个班级在“领会”层面有差异而在“应用”层面没有差异，也就意味着，课堂设计利用视觉化呈现对于学生数学理解有一定作用，有利于概念的转化、判断和推理，但在引导学生形成问题解决方案的策略意识和策略方法方面仍显不足。“应用”和“领会”的区别在于，“领会”是指当说明抽象概念的用途时，学生能够使用该抽象概念，而“应用”是在没有说明解决模式的情况下，学生正确地把该抽象概念应用于适当的情境[20]。相比“领会”，“应用”在解决问题之前需要学生判断问题解决的情境和目标，也就是学生需要多一些策略意识和策略方法才能解决问题。另外，学生的“应用”也会受到语言解读能力的影响，而视觉化呈现设计注重概念的理解，缺乏对复杂问题的关照，而且在文字语言的理解方面也没有对学生进行明确的干预和引导。由此可知，本次视觉化呈现设计对于学生概念的理解和领会具有一定的作用，在应用问题解决设计方面有待进一步提升。

六、研究结论与展望

由实验的数据与分析，可以初步确定数学知识的视觉化呈现对于内在认知负荷比较高的内容的学习显著有效，视觉化知识呈现有利于促进学生对数学概念的理解并引导学生进行有效学习，对于中等及以下学生效果尤其显著，对于学生进行有效的数学知识识记、领会以及分析能力的提升都有不同程度的作用。但由于实验中仍存在一些客观因素的干扰和实验分析手段的限制，实验结果中的数据可能还存在片面性，今后这项研究设计还应在扩大研究对象的基础上，充分结合学习者的需求以及学习内容的特征，更深入地检验数学知识视觉化呈现方法的有效性和适应性。

当前，视觉表征已经成为突破教学知识难点的重要突破口[21]，促进认知协调的教学知识呈现成为教学设计发展所趋;优化视觉表征技术，借助科学的学习分析工具，开展实证研究和实践设计，探索视觉呈现与学生认知协调之间的关系及模型设计成为未来研究所需。基于此，在本研究基础上，未来应关注知识视觉化呈现内容、形式、逻辑以及方式与学生的学习发生的作用机理，探究视觉化呈现组织对学生的学习作用程度、范围以及效果，这不仅影响着教学中的知识视觉表征技术和价值取向，也关系着学习的引导方向，对进一步促进数学理解、丰富教学设计理论与实践具有重要意义。

[参考文献]

[1] 中华人民共和国教育部.义务教育数学课程标准：2011版[M].北京：北京师范大学出版社，2012：1.

[2] 康世刚.中国西部地区中学生数学素养现状调查研究[J].数学教育学报，2014（5）：36-40.

[3] 金志成，隋洁.学习困难学生认知加工机制的研究[J].心理学报，1999，43（1）：47-52.

[4] 陈立，赵微.我国数学学习困难研究现状述评[J].中国特殊教育，2013（8）：61-66.

[5] 莫雷，张卫.学习心理研究[M].广州：广东人民出版社，2005：173.

[6] 张睆，辛自强.基于认知负荷理论的数学学优生教学[J].教育学报，2010，6（3）：59-65.

[7] 張春莉，王艳芝.数学教学中实施协同学习的策略初探[J].教育科学研究，2018，285（12）：57-62.

[8] SWELLER J.Cognitiveload during problem solving： effects on learning[J]. Cognitive science， 1988，12（2）：257-285.

[9] 李晶，郁舒兰，金冬.均衡认知负荷的教学设计及知识呈现[J].电化教育研究，2018，39（3）：25-30.

[10] SWELLWE J. Element interactivity and intrinsic， extraneous，and germane cognitive load[J]. Educational psychology review，2010（22）：123-138.

[11] MAYER R E.The Cambridge handbook of multimedia learning[M]. 2nd ed. New York， NY： Cambridge University Press，2014：151-370，346.

[12] 陈明璋，李俊仪，李健恒，杨晨意.逐步引导注意力之多媒体教学设计对圆切线性质学习之成效研究[J].台湾数学教育期刊，2016，3（2）：1-30.

[13] PAAS F， JEROEN J G， VAN M. Variability of worked examples and transfer of geometrical problem-solving skills： a cognitive-load approach[J]. Journal of educational psychology，1994， 86（1）： 122-133.

[14] 汪安圣.心理学及其在工业中的应用[M].北京：机械工业出版社，1987：29.

[15] 钟丽佳，盛群力.如何调控认知负荷“最优化”：发展综合认知能力——访谈国际著名认知科学家弗莱德·帕斯[J].现代远程教育研究，2017（4）：5-12.

[16] 理查德·迈耶.多媒体学习[M].牛勇，邱香，译. 北京：商务印书馆，2006：93，87.

[17] 林福来，黄敏晃，吕玉琴.分数启蒙的学习与教学之发展性研究[J].科学教育学刊， 1996，4（2）：191-196.

[18] 辛自强，张梅.数学学优生的认知特点及影响因素[J].中国特殊教育，2013（3）：86-91.

[19] 梁宁建.当代认知心理学[M].上海：上海教育出版社，2014：16，137.

[20] 布鲁姆.教育目标分类学（第一分册认知领域）[M]. 罗黎辉，译.上海：华东师范大学出版社，1986：139，117.

[21] 朱永海，张舒予.知识视觉表征：知识可视化的实践途径[J].电化教育研究， 2013，34（8）：17-23.