基于响应曲面的豌豆压痕加载曲线硬度测定方法试验分析

宋学锋 戴 飞 张雪坤 孙耀恒 张方圆 张锋伟*

(1.甘肃农业大学 机电工程学院，兰州 730070；2.白银矿冶职业技术学院 机电工程系，甘肃 白银 730900)

谷物是人类生存的物质基础，谷物质量的优劣直接影响谷物制粉、食品加工、种子储运等生产环节。谷物硬度是全球粮食部门严格控制谷物质量的一项重要指标。近年来，随着人们生活水平的提高以及谷物加工技术的不断发展，谷物硬度的检测在征购、生产、育种、加工、储藏、运输和消费等各个环节中起到越来越重要的作用，谷物籽粒硬度已逐渐成为世界各国区分谷物类别和贸易等级的主要依据，同时也是国内外谷物市场分类和定价的重要指标。

目前测定谷物硬度的方法建立在研磨、压碎、磨耗或压痕原理之上，根据不同的原理采用不同的测定方法。主要的硬度测定方法有角质率法[1-2]、抗粉碎硬度指数测定法[3]、研磨法[4]、SKCS测定法[5]、基因序列法[6-9]等。在现有硬度测定方法中，均以研究谷物特定数量散粒体整体的硬度性能和单籽粒整体硬度特性为衡量指标[10-11]，但这些方法均不能对谷物籽粒不同组成部位进行硬度测定，而且各种谷物硬度测定方法均有不同的衡量指标，所测定的硬度值之间很难进行横向比较。对单个谷物颗粒各组成部位的硬度检测，更能详细反映种子与硬度相关的特征和性状，所以单籽粒硬度特性及其内部不同组成部分的硬度状况必将成为育种行业重点关注的问题之一。张锋伟等[12-15]针对此问题提出了基于压痕加载曲线的谷物硬度测定方法，探究了压痕加载曲线法的加载速度、压入深度、针尖锥度等与硬度的关系，并进行了持续研究。如对西旱2号小麦的胚、胚乳、麦皮进行了硬度测定，对豌豆、玉米、绿豆进行压痕加载曲线硬度测定，结果证明该测定方法准确性较高，具有可行性，并且可以解决单个谷物颗粒各组成部位的硬度检测。本研究在基于压痕加载曲线的谷物硬度测定方法基础上，以绿豆为研究对象，根据Box-Behnken试验设计原理进行3因素3水平响应面分析法，开展压痕加载曲线试验方法作业参数的优化分析，以此探究锥尖粗糙度、四棱锥压头锥度和压头硬度3个因素对压痕曲线线性段起点比值和线性段距离比值试验指标的响应顺序，探明硬度测量值是否会受压头物理特性的影响，以期进一步完善基于压痕加载曲线的谷物硬度测定方法。

1 材料与方法

1.1 试验材料

含水率对谷物加工过程、产品品质及贮藏具有重要的影响[16-18]，而适宜加工的豌豆的含水率通常为10.3%～18.3%[19]，为此，选用市售自然干燥的的陇豌豆3号(甘肃省农业科学院培育)为试验材料(图1(a))。试验前首先采用上海音浦绿洲检测仪器有限公司生产LDS-1F电脑水分测定仪测得豌豆的含水率为13.6%。然后对试样进行打磨，使其形状为鼓形，厚度约为3～5 mm，种子内部各处质地均匀。最后使用360目的砂纸对豌豆籽粒进行粗磨，再利用400目的砂纸细磨，打磨成底座面和待测面，底座面和待测面要保持平行。打磨过程中，待测面和底座面应该与双子叶瓣结合面保持平行，以防止压头压入时导致试样沿结合缝开裂而引起测量误差，出现异常测量数值。制作好的豌豆试样见图1(b)。

在选择压头时，各类谷物籽粒大小不一且总体相对较小，小角度锥尖压头更适合尺寸较小、形状不规则的谷物籽粒。试验过程中选用不同硬度金属材料(Q235布氏硬度为30 HB，45号钢布氏硬度为57 HB，65Mn布氏硬度为61 HB)制作压头，压头形状为四棱锥，锥度分别为20°、32.5°、45°(图1(c))，锥面粗糙度分别应用1 000、1 500、2 000目进行处理。压痕深度、压入载荷、压痕曲线特性参数较易测量，将成为谷物籽粒硬度试验的衡量指标。

图1 试验样品及压头Fig.1 Test sample and indenter

1.2 试验仪器与方法

谷物压入硬度测定试验加载仪器可采用MTS(美特斯)深圳SANS(三思)公司制造的CMT2502型电子万能试验机，该试验机在试验过程中可实时动态显示压力、位移、加载速度及试验曲线，能自动计算弹性模量、屈服强度、破碎负载、最大变形等参数。试验机最大试验力为500 N，力分辨率0.01 N，位移分辨率0.001 mm；试验中，谷物及压头尺寸测定使用游标卡尺和千分尺。在硬度试验过程中，试验机做压缩加载试验时，上夹头处于移动状态，下夹头处于固定(静止)状态。试验时，下夹头选用钢制圆盘夹具，用于放置谷物试样；上夹头选用双面加紧夹具，用与夹持锥尖压头，将锥尖压头铅直夹持在上夹具正中央，压头尾部顶住夹具固定端，以防止锥尖受压时产生纵向位移。试验时，万能试验机加载速度为3 mm/min、压入深度0.4～0.5 mm。

本研究中压入方法是将特殊形状的压头借助一定压力的作用压入被测材料，对加载-卸载曲线的研究来间接得到压入深度、压痕面积等参数，进而计算出材料的硬度、弹性模量等。应用该方法不仅可以测试材料纳米尺度的硬度，而且能够很方便地测试材料在任意深度下的硬度(图2)。压头压入材料的过程中会发生弹塑性变形[20]，若压头为球形，压头下端直接接触的材料首先发生弹性变形，这一阶段被压材料的等效应力小于材料的屈服强度，材料处于弹性应力状态；之后是由弹性变形向塑性变形转变的过渡阶段，此时弹性变形和塑性变形共存，并随着压入深度的不断增大，由弹性进入塑性变形的材料体积也随之增大，但因为塑性变形的材料仍未达到自由表面，所以发生塑性变形的材料始终处于周围弹性材料的约束之中；最后是完全的塑性阶段，材料的塑性变形区已经扩展到自由表面，此时，不存在自由表面对塑性变形的弹性约束[21]。

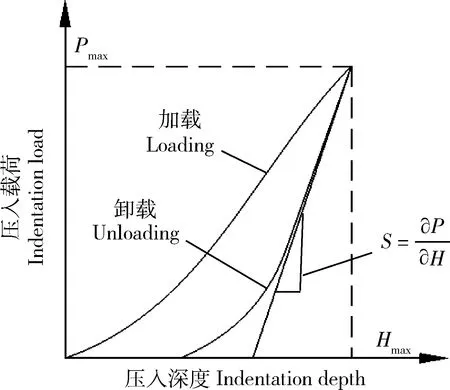
S为斜率；∂P为压入过载荷的导数；∂H为压入深度的导数。S is gradient;∂P is derivative of indentation depth;∂H is derivative of indentation load.图2 准静态纳米压入加载-卸载曲线Fig.2 Loading-unloading curves of the quasi static nanometer

1.3 试验设计

采用Box-Behnken[22-23]模型进行试验设计能减少试验次数，并达到全面分析的效果。试验过程中以锥尖粗糙度(x1)、压头锥度(x2)和压头硬度(x3)为试验因素，以压痕曲线线性段起点比值(Y1)和压痕曲线线性段距离比值(Y2)为响应值，各试验因素水平编码见表1，共实施17组响应面分析试验，试验中各项性能指标数值分别以3次重复的平均值为测试结果。

表1 压痕加载试验因素水平编码表Table 1 Factor level coding table of indentation loading test

以压痕曲线线性段起点比值为试验指标，线性段起点比值Y1的计算公式为：

(1)

式中：L1为压痕曲线线性段起点载荷，N；F为压痕曲线最大载荷，N。

由于谷物内部不同组分的厚度是一定的，因此，采用基于压痕加载曲线的试验方法时，要求压痕曲线线性段起点比值越小越精确。

以压痕曲线线性段距离比值为试验指标，线性段距离比值Y2的计算公式为：

(2)

式中：L2为压痕曲线线性段终点载荷，N。

2 试验结果与分析

对不同试验因素配置进行压痕加载曲线的硬度测试，寻求作业参数的最优组合，试验设计方案与测定结果见表2。

表2 压痕加载曲线试验的响应面分析结果Table 2 Response surface analysis results of indentation loading curve test

2.1 线性段起点比值模型建立与回归分析

利用Design-Expert软件对所得试验结果进行分析，获得编码值表示的压痕曲线线性段起点比值Y1的二次回归模型为：

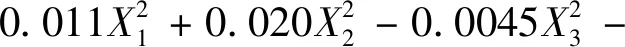
(3)

式中：X1、X2、X3分别为锥尖粗糙度、压头锥度、压头硬度的编码值。对上述二次回归模型进行方差分析和回归系数显著性检验，结果见表3。可知，回归模型的P<0.000 1，表明回归模型极其显著；失拟项P>0.05，失拟不显著，说明模型所拟合的二次回归方程与实际相符合，能正确反映线性段起点比值Y1与X1、X2和X3之间的关系，回归模型可以较好地对优化试验中各种试验结果进行预测。

根据回归模型式(3)得到各因素交互作用对线性段起点比值影响的响应面图(图3)。响应曲面的形状能够反映出交互因素作用的强弱，椭圆形表示两因素交互作用显著，而圆形则相反。由图3(a)可以看出，当压头硬度为固定的水平值时，线性段起点比值在随着压头锥度由20°～45°不断变化过程中，呈先减小后增大的趋势，且变化幅度较明显；当压头锥度固定在某一水平时，随锥尖粗糙度的增加，线性段起点比值呈缓慢减小趋势。应用基于压痕加载曲线的谷物硬度测定方法时，随着锥尖粗糙度的减小，压头锥尖压入谷物时与其摩擦阻力降低，使其能够很快进入线性段起点。由回归分析可以得出，压头锥度对线性段起点比值的影响大于锥尖粗糙度的影响。

由图3(b)可以看出，当压头锥度为固定的水平值时，锥尖粗糙度与压头硬度的交互作用对线性段起点比值的影响不明显。当锥尖粗糙度固定在某一水平时，由响应曲面可以看出，压头硬度由30～61 HB不断变化时，对线性段起点比值影响很小，锥尖粗糙度对线性段起点比值的影响大于压头硬度对其的影响。

当锥尖粗糙度为固定水平值，压头硬度为61 HB、压头锥度为30°时，线性段起点比值达到最小值(图3(c))。当压头硬度为定值时，线性段起点比值在随着压头锥度由20°～45°不断变化时，呈先减小后增大的趋势，且变化幅度较明显，压头锥度对线性段起点比值的影响高于压头硬度的影响。

图3 部分交互因素对线性段起点比值的影响Fig.3 Effects of indenter’s taper and the hardness on start point ratio of linear segment

各工作参数对线性段起点比值产生影响的多因素分析可知，3个因素对线性段起点比值影响的顺序依次为：压头锥度、锥尖粗糙度及压头硬度。

2.2 压痕曲线线性段距离模型建立与回归分析

对试验结果进行数据处理，得到锥尖粗糙度、压头锥度、压头硬度对压痕曲线线性段距离比值Y2的二次回归模型：

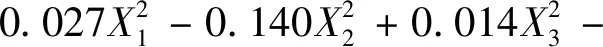
(4)

对二次回归模型(式(4))进行方差分析和回归系数显著性检验，结果见表3。可以看出回归模型的P=0.000 6，表明回归模型极其显著；失拟项P>0.05，失拟不显著，说明模型所拟合的二次回归方程与实际相符合，能正确反映线性段距离比值Y2与X1、X2和X3之间的关系，回归模型可以较好地对优化试验中各种试验结果进行预测。

根据回归模型式(4)得到各因素交互作用对线性段距离比值影响的响应面图(图4)。由图4(a)可以看出，线性段距离比值在随着压头锥度由20°～45°不断变化时，呈先增大后减小的趋势，且变化幅度较明显；当压头锥度固定在某一水平时，随锥尖粗糙度的增加，线性段距离比值变化不很明显。应用基于压痕加载曲线的谷物硬度测定方法时，压头锥度为32.5°、锥尖粗糙度为2 000目为最佳参数。由回归分析可以得出，压头锥度对线性段起点比值的影响大于锥尖粗糙度的影响。

锥尖粗糙度与压头硬度的交互作用对线性段距离比值的影响不明显(图4(b))。当压头硬度固定在某一水平，而锥尖粗糙度由1 000～2 000目不断变化时，对线性段距离比值的影响很小。所以，压头硬度对线性段距离比值的影响小于锥尖粗糙度对其的影响。

当压头锥度为32.5°时，线性段距离比值达到最大值(图4(c))。当压头硬度为一定值时，线性段距离比值在随着压头锥度由20°～45°不断变化时，呈先增大后减小的趋势，且变化幅度较明显，压头锥度对线性段距离比值的影响高于压头硬度的影响。

各工作参数对线性段距离比值产生影响的多因素分析可知，对线性段距离比值影响的顺序依次为：压头锥度、锥尖粗糙度及压头硬度。

3 结 论

本研究依据Behnken试验设计原理，以锥尖粗糙度、压头锥度和压头硬度为自变量，以线性段起点比值及线性段距离比值为响应值，探究了压痕加载曲线的谷物硬度测定方法作业参数的最优组合，主要结论如下：

1) 根据试验结果数据，建立了锥尖粗糙度、压头锥度和压头硬度与以线性段起点比值及线性段距离比值的二次回归模型，并得到方差分析数据。

2)二次回归方程与实际相符合，能正确反映线性段起点比值、线性段距离比值与锥尖粗糙度、压头锥度、压头硬度之间的关系，回归模型可以较好地对优化试验中各种试验结果进行预测。分析中得到的响应面图可反映出交互因素作用的强弱。

3)试验数据分析表明，对2个响应指标建立的回归方程均显著，压痕加载曲线线性段起点比值、线性段距离比值对谷物内部硬度测定精确度产生重要影响，对影响两者的多因素进行分析，得出 3个因素对线性段起点比值及线性段距离比值影响的强弱顺序依次为：压头锥度、锥尖粗糙度、压头硬度。试验结果对于进一步完善压痕加载曲线的谷物硬度测定方法提供了一定的理论参考。

本研究采用的不同特性压头在制作过程中较为复杂，生成的数据还需进行测量误差评价与分析，以获得更加可靠准确的数据结果。所采用的谷物压痕加载曲线硬度测定方法目前还没有研制出快速方便的谷物硬度测定设备，仅限于试验研究中使用。硬度试验机理需做进一步研究，但由研究结论可以得出，硬度测量值会受压头物理特性影响，对后续开展相关研究具有一定参考意义。