固沙装备插草圆盘前进速度与阻力关系分析
2020-09-14李艳洁寇英涛张恒宇刘晋浩
李艳洁 寇英涛 张恒宇 刘晋浩
(北京林业大学 工学院,北京 100083)
在治理土地沙漠化引起的灾害性方面,已有许多治沙措施应用于实践中[1-6],而在诸多工程治沙手段中,铺设草方格沙障是一种绿色环保的常用手段[7-9]。目前铺设草方格仍大范围采用人工作业,相比人工作业,机械铺设具有更高的效率。在机械化铺设草方格装备研究方面,由最初的 “草方格铺设机器人”[10-13],改进为“多功能立体固沙车”进行防风固沙。该装备能够实现草方格的横、纵向一次性机械化成格铺设,其中纵向插草部件是一个与固沙车作业机架相连的插草圆盘。该圆盘与固沙车等速前进的同时,以一定的下压力向前滚动,将草秆压入沙土内约20 cm。在野外沙地插草作业中发现,插草圆盘前进速度和下压力等作业参数与草方格铺设质量密切相关,因与沙土物性直接相关,缺少定量化设计依据,在作业过程中存在草秆插入深度不够导致草方格寿命降低或插草动力过大导致能耗浪费的情况。实际的插草圆盘在野外插草作业中,摸索插草圆盘的工作参数对草方格铺设质量的影响规律主要依靠大量的经验性尝试。目前对于草方格铺设装备插草质量和部件与草秆相互作用以及运动特性的研究较少[14-15],且以试验研究为主,试验中圆盘存在偏载现象导致系统误差;理论分析未涉及到纵向插草圆盘、草秆与沙土三者间复杂的相互作用及对各自运动的影响。
本研究拟对插草圆盘滚动前进插草作业中草秆的运动规律进行分析,揭示草秆运动参数与圆盘前进速度等参数间的定量关系,采用离散元法对插草圆盘的滚动前进插草进行数值模拟,分析圆盘插草阻力的影响因素及影响规律,以期为插草圆盘工作参数的合理选择提供理论依据。
1 竖直下压过程的插草试验
为对草秆运动进行数值仿真,确保仿真所采用的草秆运动参数与实际相吻合,对草秆插入沙土的过程进行了沙箱内的竖直下压式插草试验,试验装置见图1。插草圆盘在电机控制下可实现指定速度的上下匀速移动,试验中全程拍摄草秆的运动和变形,为后续标定草秆转动参数提供试验数据。试验研究发现,草秆会被圆盘分成2段,弯折发生在草秆被压入沙土过程中与圆盘接触点处,且两段草秆近乎保持直线形式绕着弯折点边下移边转动(图2(a)),期间并未有明显的弯曲变形。因此本研究将草秆简化为三段式的刚性圆柱体模型(图2(b)),即:中间与圆盘厚度相等的一小段草秆随圆盘下压而随动向下平移,左右两长段草秆则边下移边绕着弯折点同步相向转动合拢。

1.电机;2.圆盘轴;3.插草圆盘;4.草秆;5.沙箱1.Motor;2.Disk shaft;3.Inserting disk;4.Straws;5.Sandbox图1 竖直下压插草试验装置Fig.1 Experimental device for vertical inserting straw test
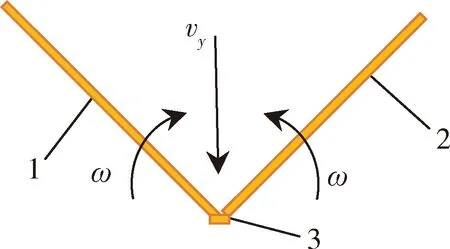
1、2、3分别为刚性草秆的第一段、第二段、第三段。1、2 and 3 are the first、second and third segments of the rigid straw.ω为草杆下压过程中的转动角速度,rad/s;vy为草杆下压过程竖直方向的速度,mm/s。ω is the rotational angular velocity during the pressing of the straw,rad/s;vy is the vertical velocity during the pressing of the straw,mm/s.图2 三段式刚性草秆模型Fig.2 Three-segment rigid model for a straw
1.1 草秆转动速度的标定
两侧长段草秆绕该端点定轴转动的速度由试验标定。当中间段草秆被压至最深处时转过角度刚好为90°,即两侧草秆刚好处于直立状态。本研究使用Adobe Premiere软件对插草试验中草秆的运动功能进行分析,认为草秆在下压的过程中近似做匀减速转动,因此利用此软件的同步对比功能,将插草仿真与插草试验进行同步比对,每隔0.5 s将仿真计算得到的草秆转过角度与插草试验的草秆转过角度对比,从而标定草秆绕端点转动的初始角速度与角加速度(图3)。
1.2 沙土扰动范围测试
本研究利用插草试验研究沙土扰动范围,采用衡量指标是相应位置的土压力。以圆刃插草盘为研究对象,工况参数及减小误差的方法与简单下压式固沙插草试验一致,沙土土床中传感器的埋设位置见图4。为探究不同位置处沙土受到插草盘的影响,选取插草盘一侧同一高度水平面上的12个位置,测量铅垂和水平方向的土压力。本试验为单因素试验测定,主要探究插草盘下压速度对沙土扰动范围的影响。
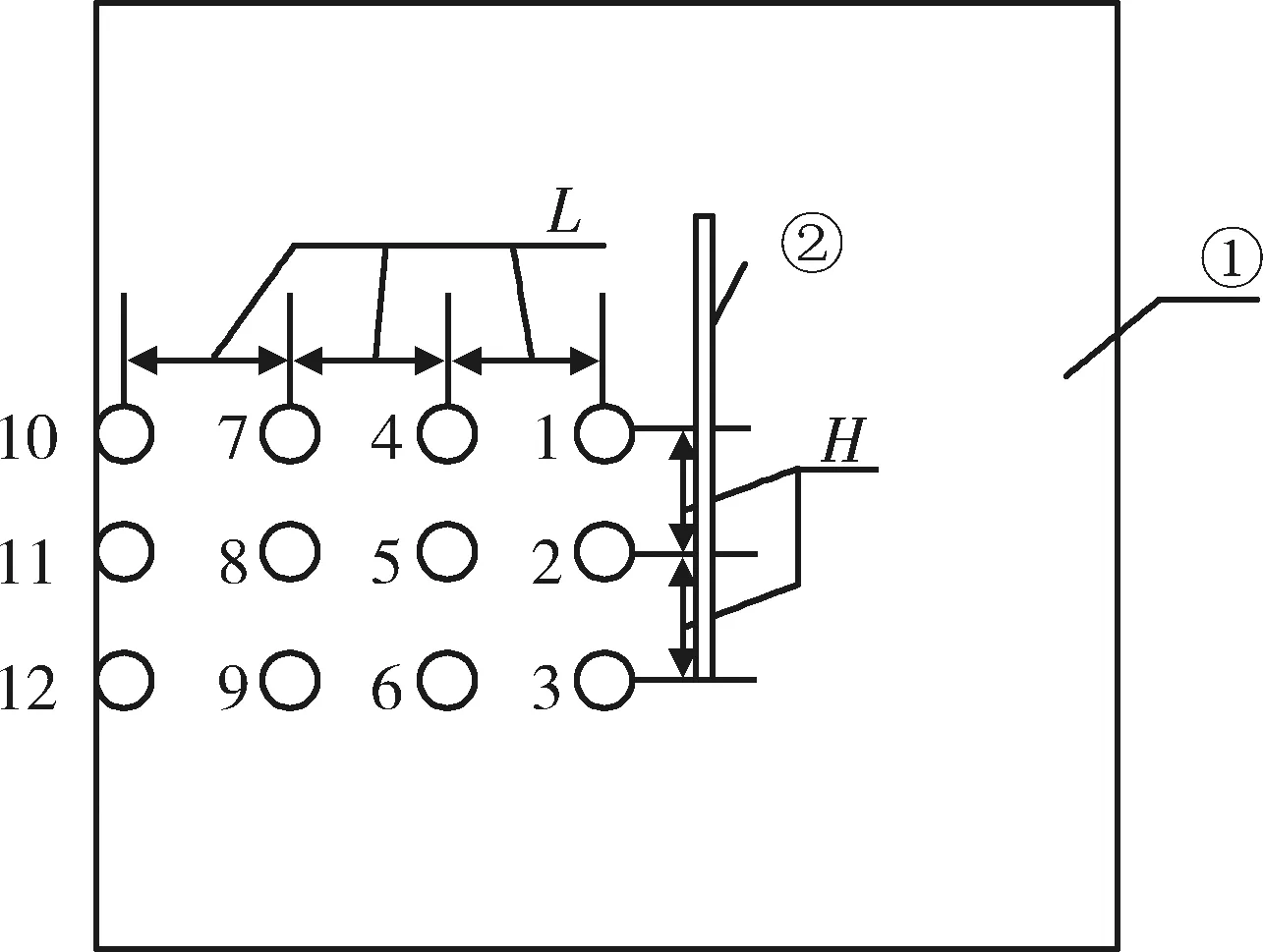
①沙箱;②插草圆盘;编号1,2,…,12为传感器。H、L 分别为相邻传感器在水平面内前后、左右的间距,cm。图5 同。① and ② are sandboxes and grass inserting discs;1-12 are sensors.H and L are the distances of adjacent sensors in two directions within a horizontal plane respectively,cm.The same in Fig.5.图4 沙土扰动范围测试示意图Fig.4 Schematic diagram of measurement of soil disturbance domain
测试结果(图5)表明:竖直方向土压力随着插草圆盘横向距离的增大而减小,且竖直方向土压力在距离插草盘20 cm处为零。产生这种现象的原因是:下压草秆直接挤压插草盘正下方位置处的沙土,而对较远位置处的沙土的挤压作用较小。图5(b)表明,随着距离插草盘越来越远,水平方向土压力会先减小后增大,且在沙槽壁面处土压力较大。这是因为,插草盘正下方的沙土受草秆挤压可向两侧移动从而减小水平压力,而壁面对沙土产生运动限制,使得壁面位置的水平土压力增大。图5表明,相同位置的竖直、水平土压力随着插草速度的增大均有逐渐增大的趋势,是因为当增大插草速度时,单位时间内的沙土挤压变形在变大,因此土压力也会随之增大。
由于本研究采用竖直下压插草试验目的是标定草秆转动速度和加速度,而非阻力的测试,因此沙箱侧壁面的边界效应对草秆的运动影响甚微可暂不考虑。
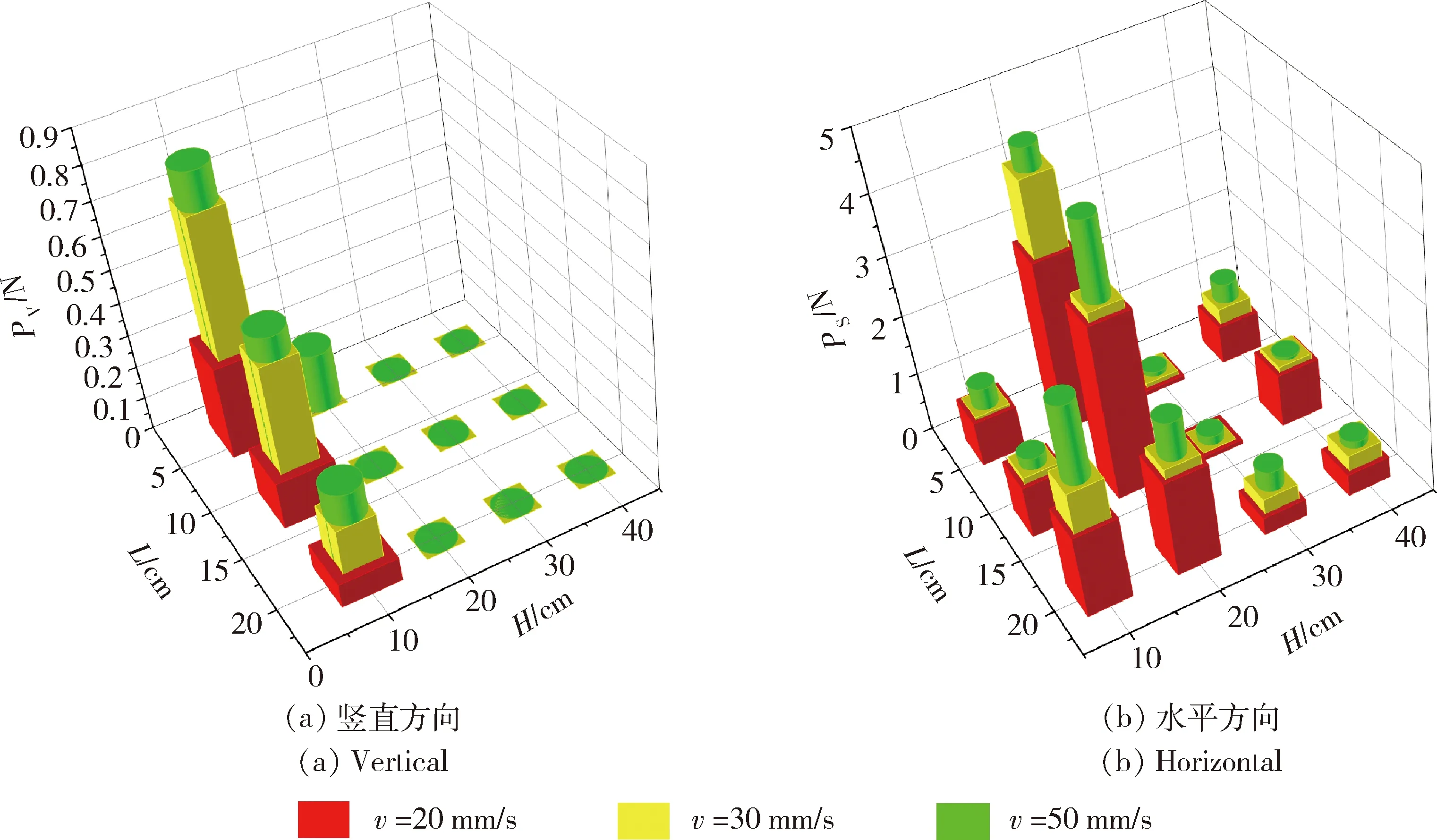
Pv,Ps分别为竖直方向和水平方向的土压力。Pv and Ps are vertical and horizontal earth pressures,respectively.图5 插草速度 (v)对沙土扰动范围的影响Fig.5 Effect of inserting velocities to soil disturbance
2 草秆在下压过程的运动分析
在插草圆盘将草秆压入沙土过程,其所受的插草阻力会受到草秆运动状态的显著影响。本研究针对插草盘作业过程中草秆的运动规律进行了理论推导,为后续的数值仿真提供理论基础。
假设一半径为R的插草圆盘滚动插草时前进速度为v,入土深度为h,平铺于地表且半径均为r的草秆一旦开始运动,在弯折点处始终与圆盘边缘接触,直到被下压至深度h(即圆盘外缘最低点)运动停止,与圆盘脱离。圆盘连续滚动插草过程中的一个阻力计算周期的运动时间ΔT为某根草秆从地表开始向下运动直到被下压到圆盘入土深度的时间段,则当圆盘连续滚动时,始终有固定根数的草秆与圆盘接触,因此插草阻力应该是保持恒定的。假设任一根草秆的运动规律均相同,单根草秆在不同时刻与圆盘的位置关系见图3,单根草秆下移运动时间ΔT由式(1)确定:
(1)

在插草作业过程中,圆盘会沿着前进方向与草秆逐一接触并将草秆逐根压入土中(图6(b))。且任一根草秆都有相同的运动规律,只是运动的开始时刻不同,即相邻两根草秆开始运动存在时间差Δt:
(2)
N=ΔT/Δt
(3)
式中:Δl为相邻两根草秆横截面圆心距。圆盘在ΔT时间内所接触的草秆数量可由式(3)确定,将式(1)、(2)代入式(3)得:
(4)
上述分析内容仅为在弯折点一小段草秆的运动规律。对于整根草秆的运动速度分2步讨论:分别是中段竖直和两侧草秆的运动速度分析。任意时刻中段草秆的竖直方向平动速度由式(5)确定:
vy=(Δy)′
(5)

(6)
式中:t为圆盘接触第i根草秆的任意时刻,当t=0时即为草秆在竖直方向运动的初速度,即
(7)
由式(7)可看出,每根草秆的下压初速度与圆盘前进速度v成正比例关系。
本研究在分析两侧草秆的速度时,将其平面运动分解为中间端点竖直方向的平动与绕该端点定轴转动。其中,侧段中间端点竖直方向平动速度等于中间段草秆的速度,可由式(6)确定。

位置1,圆盘与草秆i刚接触时的位置;位置2,圆盘与草秆i接触的任意位置;位置3,圆盘将草秆i压入至最深处,即等于圆盘入土深度h时的状态;位置4,圆盘与第i+1根草秆刚接触时的位置。y、x分别为第i根草秆在某时刻圆盘与草秆截面圆心间的竖直和水平距离,y0、x0分别为圆盘和草秆刚接触时的圆盘与草秆圆心间的竖直和水平距离;Δl为相邻草秆横截面圆心距;v为插草圆盘前进速度。Position 1,the position where the disc has just contacted the straw stalk i;Position 2,any position where the disc makes contact with the straw stalk i;Position 3,the disc presses the straw stalk i to the deepest point,which is equal to the depth of the disc into the soil at h;Position 4,the position of the disc when it just touchs the i+1th straw.y and x are the vertical and horizontal distances between the ith straw at the disc and the center of the straw cross section at a certain moment,and y0 and x0 are the vertical and horizontal distances;Δl is the center-to-center distance of the cross section of the adjacent straw;v is the forward speed of the inserted disc.图6 插草圆盘与草秆位置关系Fig.6 The relationship between the inserting disk and the straw
3 数值模型
插草圆盘是草方格铺设装备关键的纵向插草部件,本研究采用离散元软件EDEM对草秆-沙土进行3D建模并分析阻力。计算颗粒的法向和切向接触力分别采用Hertz和Mindlin-Deresiewicz理论[16],颗粒接触的法向力Fn和切向力Ft由式(8)确定:
(8)


(9)
由于仿真涉及颗粒规模较大,而颗粒数量对计算效率的影响十分显著。为了在不影响计算真实性的前提下减小颗粒规模,本研究建立的长方体形状沙土床尺寸为500 mm×320 mm×300 mm,且将其壁面设置为循环边界[17]以消除边界效应,在计算域通过落雨法生成沙土床,在生成的沙土床表面生成单层排列的草秆,相邻草秆之间相互独立且无间隙。草秆总长400 mm,草秆总数量为32根。料床和草秆几何模型见图7。沙土、草秆和底板的相关物性参数见表1,其中物性参数取值来源于材料手册[18]或相关文献[19]。
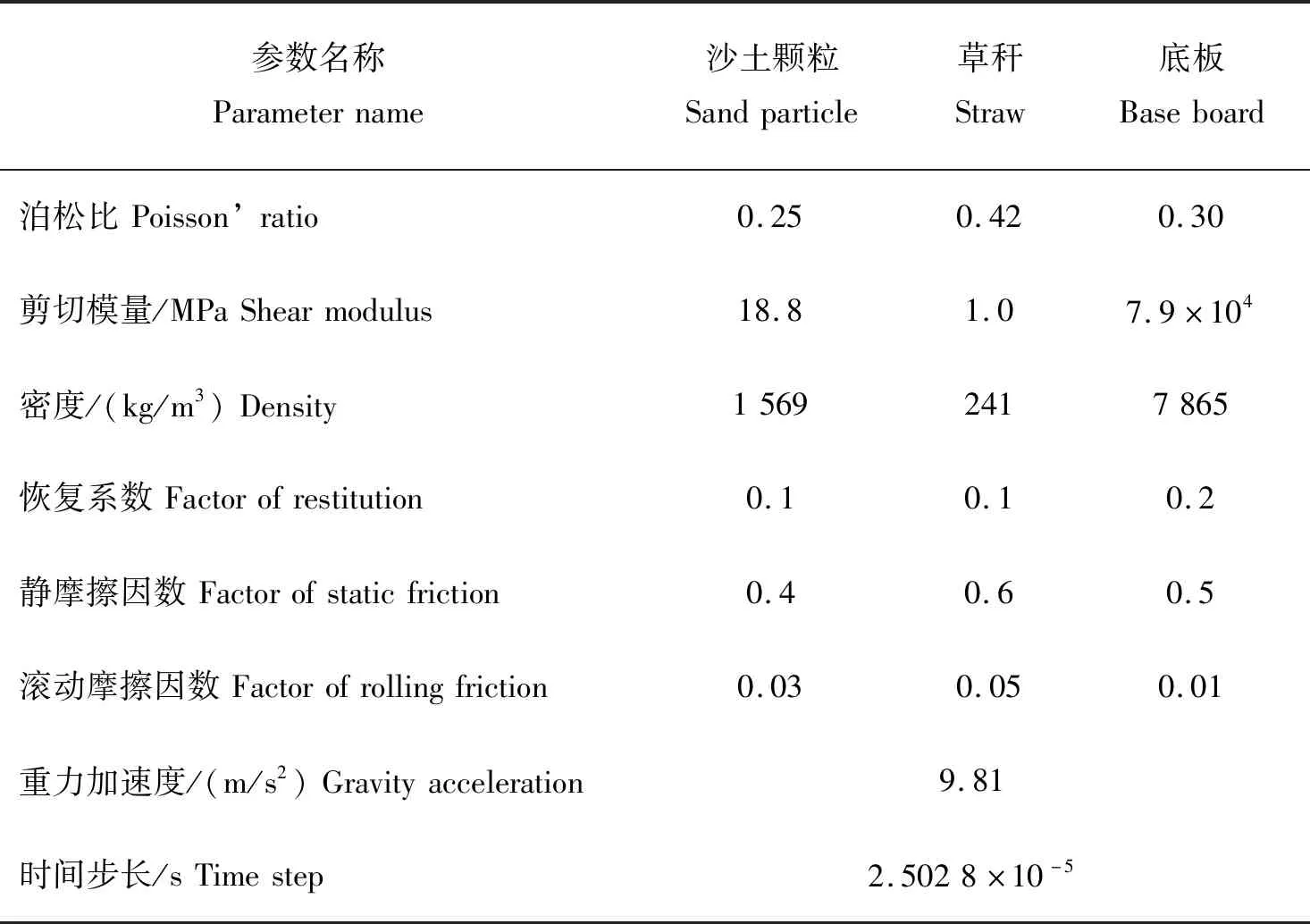
表1 仿真模型物性参数Table 1 Physical parameters used in the simulations
本研究通过DEM模拟分析圆盘的前进速度、草秆铺设密度及圆盘厚度在插草圆盘作业过程中对圆盘竖直方向插草阻力的影响规律,式(1)、(2)、(4)和(7)可用来确定单根草秆运动时间、相邻草秆运动的时间间隔、圆盘接触的草秆数量和草秆运动的初速度,仿真工况参数取值见表2。仿真中插草圆盘半径R和入土深度h分别为360 mm和200 mm。

表2 插草过程仿真工况参数Table 2 Parameters of simulation conditions of straw inserting

1.草秆;2.颗粒;3.刚性底板;4.循环边界1.Straws;2.Particles;3.Rigid base;4.Periodic boundaryL、W和H分别为颗粒料床的长、宽和高,mm。L,W and H are respectively the length,width and height of the granular bed,mm.图7 料床和草秆几何模型Fig.7 Granular bed and straw geometry model
在本研究的仿真中,由于存在软件参数设置及仿真效率的问题,需要对式(6)确定的2种插草圆盘前进速度的草秆下压速度进行线性拟合,结果见图8;根据式v=v0-at可求得线性拟合点的取值,当圆盘前进速度为4.0、5.5、7.0、8.5和10.0 cm/s时,相应的v0分别为5.868 7、8.074 9、10.277 5、12.487 1和14.697 3 cm/s;a分别为0.804 9、1.523 7、2.467 0、3.637 1和5.042 9 cm/s2。由图8 可见,圆盘前进速度越快,草秆向下压入的平移速度曲线越陡,说明草秆速度变化越剧烈。

图8 草秆中段下压速度曲线及线性拟合结果Fig.8 Velocity curves and their linear fitting results of the central segment of straws
4 模拟结果及讨论
由草秆运动理论分析可知,在1个周期内,与圆盘接触的所有草秆的运动规律可由圆盘插草过程的仿真计算得到(图9和图10),可见,随着插草圆盘与草秆逐渐接触,草秆中段在竖直方向做平移运动,两侧草秆绕着与中间段的接触点做相对合拢的转动;而且,草秆的运动在与插草圆盘刚接触时的变化比较明显,草秆入土越深,中段在竖直方向的位移以及两侧草秆转动的角度越小。

图9 草秆在不同时刻(t)的运动状态Fig.9 Straw movement at different times
图10 圆盘水平前进后草秆的状态Fig.10 The state of the straw after the disk is advanced horizontally
插草圆盘的插草阻力是由圆盘与所有接触草秆的法向力在竖直方向的力投影后求和所得,即:
(10)
式中:F为插草圆盘竖直方向阻力;Fni为每根草秆给圆盘的法向压力;N为插草圆盘在稳定插草过程中所接触的草秆数量;θi为每根草秆给圆盘的法向压力与竖直方向的夹角。由式(10)可见,插草阻力与圆盘在插草过程中所接触的草秆数量有关。大圆盘接触的草秆根数多于小圆盘,因此在其他条件相同的情况下,大圆盘滚动插草的铅垂阻力要大于小圆盘。但插草阻力受圆盘直径变化的敏感度有限。
4.1 前进速度对插草阻力的影响
通过对比插草圆盘滚动前进时不同前进速度对圆盘竖直方向插草阻力的影响关系(图11)发现:根据阻力变化特性,可将阻力变化分为2个阶段:线性增大阶段和稳定波动阶段。在线性增大阶段,圆盘前进速度越大,阻力增大得越快;但是当增大到某一最大值后,在最大阻力值附近波动而不再继续增大。此处所指的稳态为圆盘在连续滚动前进过程中连续插草时的状态,即与圆盘接触的草秆数量达到稳定值。初步分析阻力随圆盘前进速度变化而产生的这种现象的原因:随着圆盘不断的下压,与圆盘接触并被下压入土的草秆数量逐渐增多,因此圆盘竖直方向所受的插草阻力也逐渐增大。但是当与圆盘接触的草秆数量达到最大值后,则不再增加,此时圆盘所受的插草阻力也随即进入稳定的阶段。从图11中稳定波动阶段的阻力对比可知,在此范围内的前进速度对其竖直方向的插草阻力几乎没有影响,阻力最大值(即稳态值)分别为228.4、231.2、228.7、230.1、231.1 N。初步分析产生这种现象的原因是:其一,对一根草秆受力状态进行分析,在插草圆盘对草秆进行下压时,插草阻力随草秆下压深度增大而增大,而草秆最终下压的深度是相同的,因此每根草秆所受到的沙土阻力近乎是一样的,竖直方向的插草阻力在圆盘连续向前滚动插草时也只与插草深度和接触草秆数量直接相关;其二,由于本研究所关注的插草阻力是圆盘接触的草秆在竖直方向所受压力的合力,因此竖直方向的插草阻力几乎不受插草圆盘前进速度的影响。其中插草圆盘所接触的草秆数量也不会随着铺设速度的改变而变化。文献[14]通过试验探究了2.8~11.2 cm/s的插草圆盘前进速度对竖直方向插草阻力的影响,与本研究结论一致。
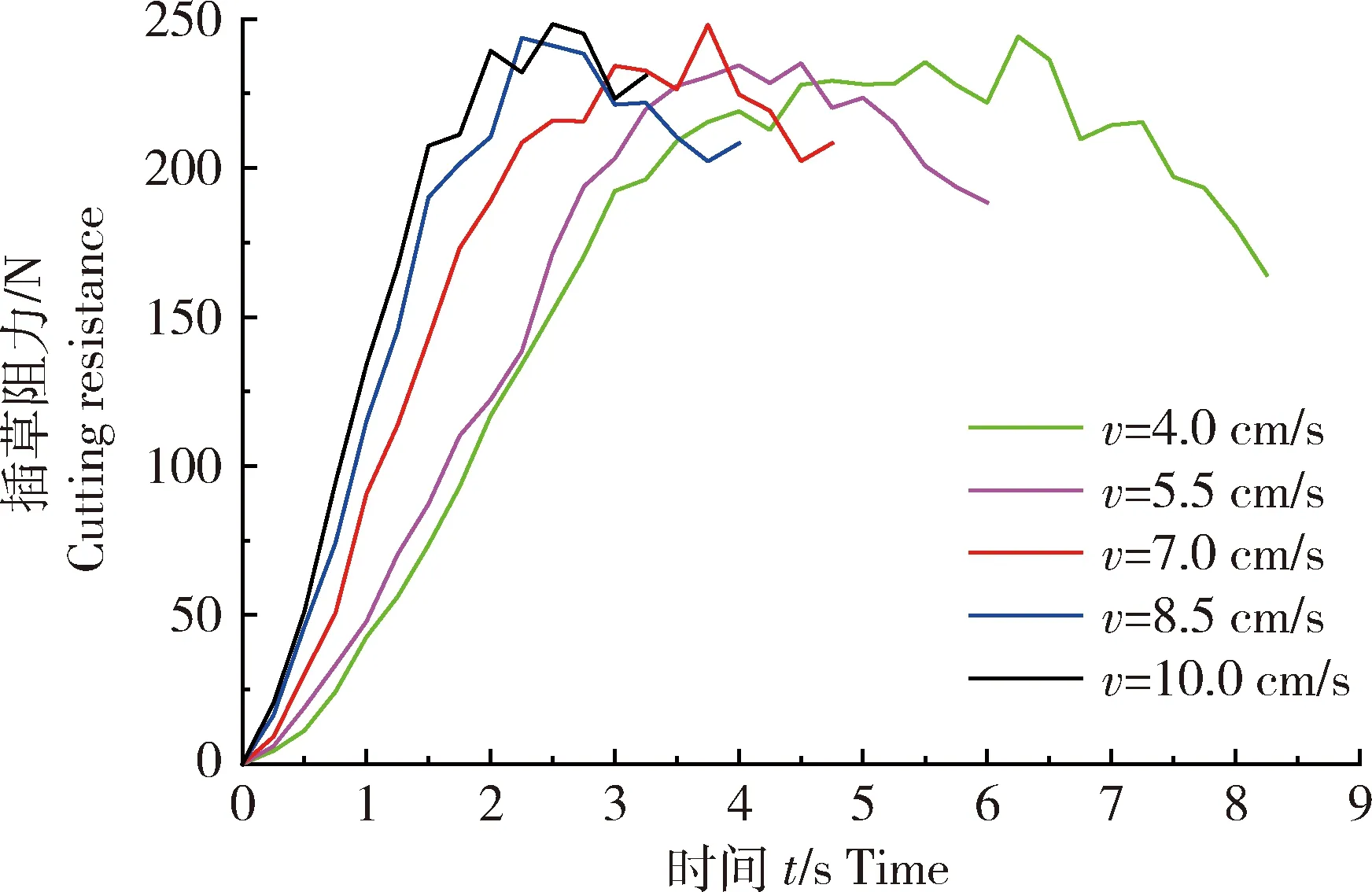
图11 不同速度(v)在竖直方向上的圆盘插草阻力的对比Fig.11 Comparison of disc insertion resistance at different speeds in the vertical direction
4.2 草秆铺设密度的影响
本研究中定义的草秆铺设密度为单位距离上铺设草秆的根数,主要对比分析了2种不同铺设密度的插草阻力。研究发现草秆铺设密度越大,插草阻力也就越大。当铺设密度分别为为100根/m和50根/m 时,其稳态插草阻力分别约为228.4和159.6 N(图12)。初步分析产生这种现象的原因为,当铺设草秆密度较大时,圆盘与草秆所接触的折弯点处会随着草秆的刚度增大而转动减缓,因此在插入相同深度时草秆的法向挤压力受到两侧沙土的作用时会增大,这种法向挤压力在竖直方向的分力也因草秆与水平夹角变小而更大,草秆受到增大的沙土阻力会传递给圆盘,即圆盘所接触草秆在竖直方向土压力的合力为插草阻力,因此,圆盘插草阻力随着草秆铺设密度的增大而增大。
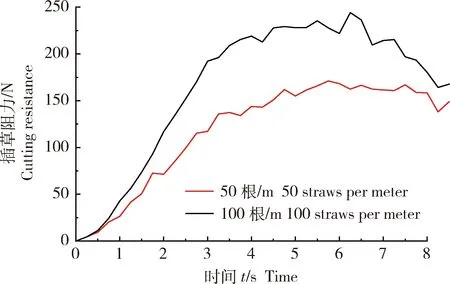
图12 2种草秆铺设密度下刀盘竖直方向的插草阻力Fig.12 Comparison of straw inserting resistance between different straw laying densities
5 结 论
本研究采用试验与数值模拟结合的方法分析了立体固沙车纵向插草圆盘插草过程中草秆和圆盘的运动与插草阻力间的关系,为草方格铺设机械化过程中部件的工作参数选取提供了一定的理论依据。初步得到如下结论:
1)草秆可用三段式刚体来简化,且每根草秆的运动规律相同,为两长段部分绕中间段做匀减速定轴转动的复合平面运动与中间部分在竖直方向做匀减速平移;
2) 当圆盘的前进速度位于4~10 cm/s区间时,前进速度对竖直方向的插草阻力影响较小,为了解决实际插草过程中草秆插入深度不够的情况,前进速度与圆盘水平方向阻力的定量关系需后续继续深入研究,以选择提高草方格铺设效率最合适的前进速度;
3)随着草秆铺设密度的增多,圆盘在竖直方向上的插草阻力增大,因此在满足固沙效果的条件下铺设草方格的草秆厚度不宜过厚。
