本科论文答辩中专家-学生匹配分组模型及算法

狄卫民， 徐文君， 王 然

（郑州大学管理工程学院，郑州450001）

0 引 言

本科毕业论文直接反映了本科生的文字表达能力、知识应用能力和综合创新能力，间接反映了指导教师的指导效果和教学水平［1-2］。毕业论文答辩是审查毕业论文质量的重要形式，越来越受到导师、学生和教学管理部门的重视［3］。在本科教学实践中，往往需要在短时间内集中完成所有毕业生的论文答辩任务。面对这种情况，当同一专业的学生较多时，经常将答辩评议专家和答辩学生事先分组，然后再安排各组学生同时进行答辩。显然，科学的分组方法是做好答辩工作的重要前提。对于分组问题，为了实现项目申请书与评审专家的自动匹配，毛晚堆等［4］提出了利用二部图谱划分异构对象的分组匹配算法。为了提高分组效率，避免分组差异引起的面试结果偏差，陈媛等［5］建立了综合面试问题的双目标均衡分组模型。为了减少社会化考试中的阅卷差错，提高阅卷速度，汪定伟等［6］建立了评卷人分组的非线性0-1 整数多目标规划模型，设计了模型求解的遗传算法。这些成果为答辩分组提供了理论借鉴。针对小规模答辩分组问题，曹莉等［7］基于回避原则和均匀原则，探讨了寻求最佳分组方案的单目标优劣交叉微分进化算法，但是没有建立分组问题的数学规划模型。方刚等［8］建立了研究生答辩分组和组内评审指派的两阶段非线性整数规划模型，并利用Lingo 软件求解该模型，取得了良好效果。不过，本科论文评审制度和答辩规则与研究生不尽相同，无法利用研究生分组答辩模型解决本科答辩问题；另外，研究生答辩时经常按研究方向分批或集中进行，同时答辩的人数较少，便于利用优化软件解算分组模型，而本科生答辩时往往按专业集中进行，同时答辩的人数较多，答辩分组问题规模较大，不利于优化软件的直接利用。以往研究为合理分组打下良好基础，但是当同时考虑导师和学生的公平性要求时，答辩评议专家与答辩学生的匹配关系将更加复杂，还需结合决策顺序进一步优化分组方案。考虑以上情况，本文根据本科论文答辩问题的特点，建立了答辩评议专家和答辩学生匹配分组的两阶段序贯决策模型，为快速得到分组结果，设计了模型求解的混合遗传算法。

1 问题描述

假设某专业的m 名学生已经在n 位教师的指导下完成毕业论文，计划分g 组同时答辩。该专业有b个研究方向，通过调查，已经获知论文i（即学生i的论文，i ＝1，2，…，m）对方向d（d ＝1，2，…，b）的隶属程度n）对方向d的熟悉程度βjd（0≤βjd≤1）。根据教务处“一个答辩评议组由3 ～5 名答辩评议专家构成”的规定，确定了各答辩评议组的专家人数nk（k ＝1，2，…，g）。根据该专业“答辩评议专家均由指导教师担任”和教务处“一个答辩评议组至少含有2 名高级职称专家（含副高和正高）”的规定及担任答辩评议专家的其他要求，已经从指导教师中挑选出了不少于2g个具有前的任务是如何对这些答辩评议专家和答辩学生进行合理分组。

2 专家-学生匹配分组模型

以往制订分组方案时，通常以所有论文相对于其答辩评议组的研究方向匹配度之和最大化为目标进行专家和学生的组别划分。实际上，这种分组方法仅能提高论文与答辩评议组之间的平均匹配程度，很难保证最小匹配度的有效性。众所周知，论文内容与答辩评议专家的研究方向越吻合，答辩评议组给出的论文评价结果越可靠。若最小匹配度过低，说明有学生分配到了答辩评议组不太熟悉其论文内容的答辩组中。此种情形下，该答辩评议组很难客观评价其论文质量，可能导致答辩中的相对不公平。为解决这一问题，本文首先求得可以满足分组约束的最大的最小论文匹配度；若该最小匹配度符合要求，再在确保此最小匹配度的前提下，寻找最大的平均论文匹配度。

另外，学生答辩时，不同专家的给分尺度存在差异但又不易统计（尤其存在首次担任答辩评议专家的教师时），这种差异将最终导致答辩评议组之间的给分差异。于是，对于一名学生而言，若将其分配到不同的答辩组中，即便相应答辩评议组同样熟悉其论文内容，也很难得到相同的答辩成绩。对于导师而言，若将同一导师指导的学生集中分配在少数几个答辩组中，则难以充分比较导师之间的指导效果，不便根据学生答辩成绩客观评价导师们的指导水平。极端情况下，若将一位导师的学生全部分配在一个给分最为“严厉”的答辩组中，还可能影响其考核结果（尤其存在答辩未通过学生时），进而导致导师之间的相对不公平。针对这一问题，考虑到专家-学生协同分组需要，本文建模时将同一导师的学生尽量分在了多个答辩组中。

为了建立专家-学生匹配分组的两阶段序贯决策模型，下面首先分析约束条件，然后给出目标函数。

2． 1 约束条件

（1）被选为答辩评议专家的导师将被分配在某个答辩评议组中，未被选中的导师不会分配在任何答辩评议组中，有：

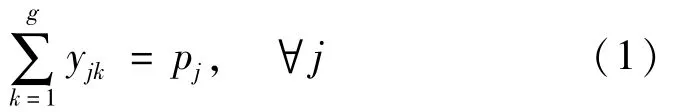
式中：pj为导师j是否被选为答辩评议专家，是取1，否取0；yjk为决策变量，表示导师j 是否分配在第k 个答辩评议组中，是取1，否取0。

（2）各答辩评议组中，专家数量应符合要求且至少含有2 名高级职称专家，有：

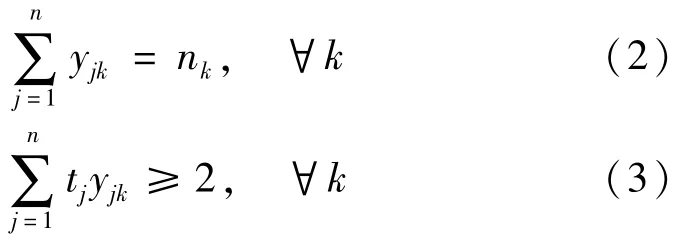
式中：tj为导师j是否具有高级职称，是取1，否取0。

（3）每个学生仅能分配在一个答辩组中，有：

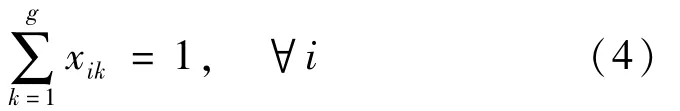
式中：xik为决策变量，表示学生i是否分配在第k 个答辩组中，是取1，否取0。

（4）学校建议了学生答辩时的论文陈述时间和专家提问时间，因此一个答辩组的工作时间主要取决于该组的学生数量。为了平衡各答辩评议组的工作时间，每个答辩组的学生数量应尽量相等（即答辩组之间的学生数量差值不能超过1），有：

式中：符号·和·分别为小于“·”的最大整数和大于“·”的最小整数。

（5）由于答辩评议专家不可避免地存在系统性评分差异（如评判基准分差异、优劣程度的给分区间差异等），因而难以根据不同组的学生答辩成绩直接判断组间论文质量的优劣［9］。为便于客观反映导师们的指导效果，方便导师之间的相互比较，此处将同一导师的学生尽量均匀地分布在多个答辩组中。同时，还须坚持导师回避制度，即每名学生均不能分配在与自己导师所在答辩评议组相对应的答辩组中。综合以上要求，有：

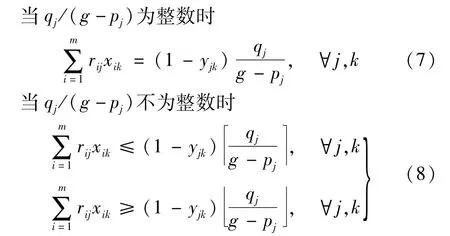
式中：rij为导师j是否为学生i 的指导教师，是取1，否取0；qj为导师j指导的学生数量。

（6）论文i对方向d 的隶属程度为αid，导师j 对方向d的熟悉程度为βjd，因此导师j 对论文i 的熟悉若将学生i分配在第k答辩组中，则第k答辩评议组对论文i 的熟悉程度可量化为该评议组专家对论文i 的平均熟悉程度，即于是，若称该平均熟悉程度为论文i与其答辩评议组的研究方向匹配度，简称论文i的匹配度，并记s0为所有论文中的最小论文匹配度，有：

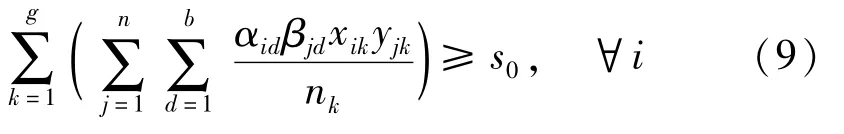
（7）考虑各决策变量的现实意义，有：

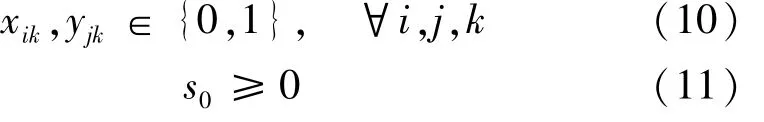
2． 2 目标函数

（1）第一阶段使最小论文匹配度最大化，有目标函数：

求解该模型，可以得到最佳的专家-学生匹配分组方案。

3 模型算法

3.1 总体思路

由于式（9）、（13）～（14）均含有关于决策变量的非线性表达式，并且在第一阶段s0为连续型决策变量，故第一阶段的模型属于非线性混合整数规划模型，第二阶段的模型属于非线性纯整数规划模型，两阶段序贯决策模型整体上属于非线性整数规划模型。一般地，对于规模较小的非线性规划问题，可以利用优化软件（如Lingo、Matlab 等）直接求解［10-11］；但是，当问题规模稍大时，不便直接解算，当同时含有整数决策变量时，求解难度更大。本文模型均为含有整数变量的非线性规划模型，不宜直接利用软件求解。但是，如果给定专家分组方案，即把yjk变为常量，那么，第一阶段的模型便成了线性的整数规划模型，能够大幅度降低求解难度。由于同一专业的学生数量不会过多（例如不超过210 人），经测试，利用Lingo12 软件可以快速求解这类线性整数规划模型（测试时，假设学生数为210，专业方向数为5，答辩组数分别为5、6 和7，每组专家数分别为4 或5，随机产生专家分组方案；利用Lingo12 求解，所有模型均可在数10 s内得到结果，其中绝大多数模型数秒得到结果；但是，当利用Matlab R2015b的相应函数intlinprog 解算模型时，运算时间较长）。考虑遗传算法（Genetic Algorithm，GA）特点［12］，对于第一阶段的决策模型而言，如果用GA 中的染色体代表专家分组方案并通过一定方法产生染色体（即给定专家分组方案），那么，利用Lingo软件便可得到各代种群中相应于不同染色体的学生分组结果和对应目标函数值；这样，结合GA 迭代寻优过程，能够得到较为理想的最小论文匹配度。在第二阶段模型中，由于以约束条件式（14）替换了第一阶段模型的式（9），其可行域较比第一阶段模型大幅度缩减，不利于GA的寻优运算。考虑序贯决策要求［13-14］，通过染色体库把两个阶段的决策联系起来，然后将染色体库中满足式（14）且使目标函数式（13）最大的染色体作为第二阶段的满意染色体，进而得到专家-学生的满意匹配分组方案。这样，便形成了以染色体库为纽带、嵌入线性整数规划精确算法（由Lingo软件实现精确计算）的混合遗传算法。

3.2 第一阶段模型算法

第一阶段寻找最大的s0，主要步骤如下［15］：

3.2.1 生成初始种群

令每条染色体代表一个专家分组方案，每个基因对应一个专家编号。亦即，染色体由被选中导师的编号构成，长度为n′，其中前n1个编号对应分配在第1个答辩评议组中的专家，第（ni-1+ 1）～第（ni-1+ ni）个编号对应分配在第i（i ＝2，…，g）个答辩评议组中的专家。这种染色体满足式（1）、（2）的要求，并且据其可以得到yjk的值。随机产生规定数量的染色体，形成初始种群。

3.2.2 计算适应度值

对于一条给定的染色体，首先判断其是否在染色体库中。如果在库中，则根据库中记录得到与其对应的模型目标值。如果不在库中，则判断其是否满足式（3）。如果不满足，令模型目标值为一个充分小的数；如果满足，利用Lingo软件（主要是应用其分支定界精确算法）求解以式（12）为目标函数、式（4）～（11）为约束条件的决策模型，得到模型目标值（已知该模型一定有最优解）［16］。然后，将该染色体及其模型目标值录入染色体库。当计算完一代种群中所有染色体所对应的模型目标值后，利用压差为2 的线性排序方法、按照目标值越大越适应环境的原则，计算每条染色体的适应度值［15］。

需要注意的是，在向染色体库录入染色体时，为避免染色体重复，应将染色体内各答辩评议组中的专家编号分别由小到大重新排序，然后再按照各答辩评议组中第1 位专家的编号大小，对各答辩评议组的顺序进行重新调整（答辩评议组中第1 位专家的编号越小，该答辩评议组的编号也越小）。在使用染色体库时，必须考虑这个规定。

3.2.3 遗传算子操作

（1）选择。根据随机遍历抽样算法，结合代沟技术，从当代种群中挑选出作为父辈的部分染色体。

（2）交叉。为生成不同的子代个体，根据交叉概率对选出的多对父辈染色体进行两点交叉。每对染色体交叉时，首先在区间［1，n′］上随机确定交叉段的起点p1和终点p2，然后互换两条染色体的p1～p2基因段，若新换入的基因段中含有原染色体保留部分的专家编号，则参照原染色体中的基因对应关系修正这些编号，进而形成两个子代个体（见图1）。此处以图1（b）所示染色体1 中重复编号8 的修正为例，说明单个重复编号的修正过程。在该染色体1 中，新换入基因段中的8 对应原染色体中的6，但6 也在新换入的基因段中，于是寻找新换入基因段中的6 所对应的原染色体中的专家编号；该编号为5，并且5 不在新换入的基因段中，于是用5 替换原染色体保留部分中的8，至此完成编号8 的修正过程。

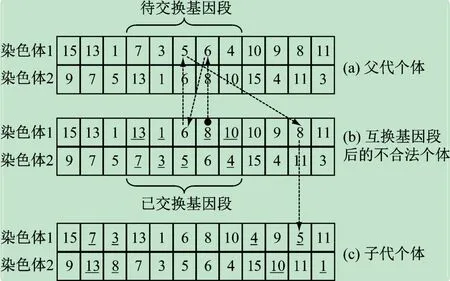
图1 染色体两点交叉示意图

（3）变异。按照变异概率在子代种群中选择需要变异的个体，进行单点变异。单点变异时，首先在染色体中随机确定一个变异基因，并记下该基因对应的专家编号；然后随机产生一个其他评议组的专家编号，并互换这两个编号位置，进而形成变异个体（见图2）。

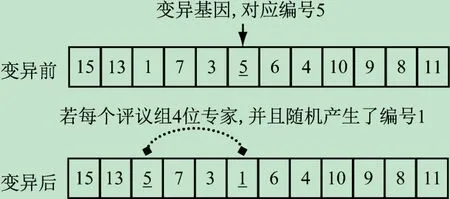
图2 染色体单点变异示意图

（4）重组。按照代沟设置比例将父代种群中的个体精英保留下来，从而获得完整的子代种群［15］。

3.2.4 继续或终止运算

循环迭代计算适应度值和遗传算子操作，以便获得最大的最小论文匹配度。如果迭代到了最大允许进化代数或者最优目标值在规定代数内没有变化，则终止运算，此时的最佳目标值就是最小论文匹配度的满意值。如果该值满足实际要求，可将其作为s0*。

4 模型及算法应用

某辅修专业的201 名本科生在38 位教师的指导下完成毕业论文，计划分6 组同时答辩。该专业有5个主要研究方向。在统计每篇论文的具体方向时，要求学生结合实际情况最多填写3 个方向；若某论文隶属多个方向，则重要方向写在前面，同时备注各方向隶属度。在统计教师熟悉程度时，对每个方向给出了非常熟悉、较熟悉、一般、不太熟悉和不熟悉5 个选项，相应量化值为1、0． 8、0． 6、0． 4 和0。根据相关规定，为每个答辩评议组分配4 位专家，已确定24 位专家人选。

利用Matlab R2015b编写混合遗传算法程序。在程序的核心代码中，应用批处理命令调用了Lingo12的Runlingo． exe 可执行文件，利用文本文件实现了Matlab与Lingo之间的数据传递；另外，还根据需要，调用了英国设菲尔德（Sheffield）大学的Matlab GA 工具箱。GA参数设置为：种群个体数目40，最大进化代数50，交叉概率0． 6，变异概率0． 1，代沟系数0． 95。连续运行5 次第1 阶段程序，依次得到满意目标值0． 705、0． 72、0． 715、0． 72 和0． 71。其中，第2 次进化过程见图3。取其中的最好值0． 72 作为最大的最小论文匹配度。经研究，该最小匹配度符合现实要求，可转入第2 阶段的程序运算。在第2 阶段，统计结果显示，在染色体库中有6 个个体的最小论文匹配度为0． 72，其中的最大平均论文匹配度为0． 844 2。这样，根据平均论文匹配度为0． 844 2 的个体便可得到专家与学生的满意匹配分组方案。该方案中，有2 名学生的论文匹配度为0． 72，5 名学生的论文匹配度为1，论文匹配度分布情况如图4 所示。

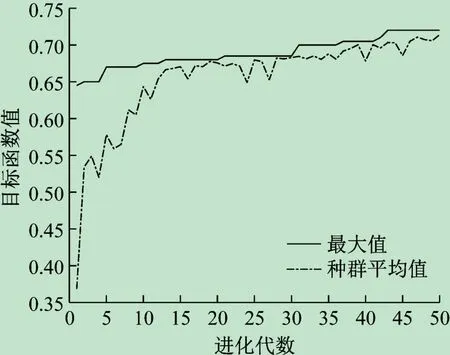
图3 第1阶段第2次运算的进化过程

如果仅以平均论文匹配度最大为目标制订分组方案，利用混合遗传算法解算以式（13）为目标函数、式（1）～（8）和式（10）为约束条件的非线性整数规划模型，可以得到最大的平均论文匹配度0． 882 1（进化过程见图5），该值大于0． 844 2，但此时的最小论文匹配度仅为0． 42，很难满足现实要求。可见，本文方法是切实可行的。

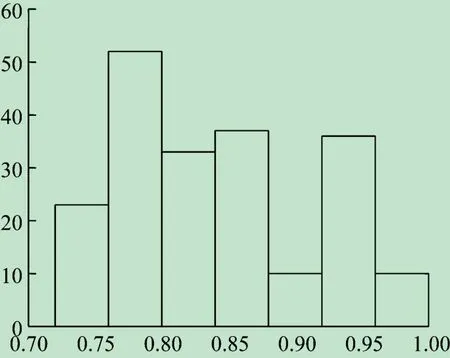
图4 论文匹配度直方图

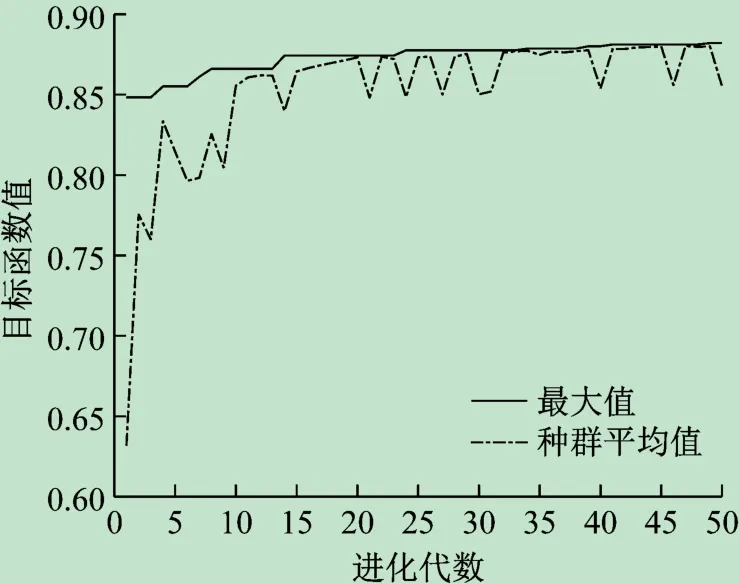
图5 仅追求最大平均论文匹配度的进化过程

5 结 语

本科毕业论文答辩是本科教学实践中的重要一环，论文答辩成绩关系到学生和指导教师的切身利益，是衡量专业教学效果的重要依据。为培养合格人才，提高教学质量，有必要对本科毕业论文答辩问题进行精准管理。为做好答辩评议专家和答辩学生的匹配分组工作，建立了两阶段序贯决策模型，提出了求解模型的混合遗传算法，并对其进行具体应用。应用结果表明，模型和算法是切实可行的。本文的答辩评议专家均为指导教师，当某些专家不是指导教师时，仅需将他们排在指导教师后编号，模型和算法同样适用；另外，当学生过多时，可以先将学生分成若干个200 人以下的大班，然后再利用本文方法制订每个大班的具体分组方案。答辩成绩反映了专业教学效果和导师指导水平，今后可以结合答辩成绩完善相关教学管理制度。