浅地表电磁探测中的匹配滤波技术应用

2020-09-14周逢道王绪磊

实验室研究与探索 2020年8期

周逢道，王绪磊

（吉林大学a．仪器科学与电气工程学院；b．国家地球物理探测仪器工程技术研究中心，长春130061）

0 引言

在浅地表电磁探测中，频率域电磁探测法具有高效、可控的优点，得到了广泛应用。其探测原理是利用涡流效应，使用发射线圈向周围发射一次场，通过接收线圈接收地下金属目标激发的二次场，以二次场的变化情况来识别地下金属目标的方法［1-2］。在实际应用中，为提高探测效率，通常采用多组收发线圈同时工作，同步收发的模式［3-5］。这种模式增加了系统的单次探测面积，可以快速采集大量的二次场信息，在大大提高探测系统工作效率的同时，也增加了系统进行数据处理所占用的时间，降低了系统的时效性［6］。而浅地表电磁探测实际应用中又对实时性有着极高的要求，因此，一种高效快速的数据处理系统显得尤为必要。

在整个电磁探测系统的数据处理系统中，需要对采集的二次场信息进行数据的处理与分析，其过程包括对模拟信号的滤波与放大、AD 转换、数字滤波等，然后判定所得的二次场信息中是否含有金属目标信号，实时反馈给控制系统。这其中，数字滤波主要对AD转换后的数字信号进行滤波与分析，直接影响了地下目标物的判定，是极其重要的一个环节。数字滤波能够克服随机误差，提高信号质量，为金属目标的识别提供更加可靠的判据。相较传统的模拟滤波器，数字滤波器具有响应速度快、精度高、稳定性好和可靠性高的优点，它通过软件实现，不需要搭建模拟电路，避免了阻抗匹配的问题［7］，降低了电路的复杂性和仪表的设计成本［8］，是浅地表电磁探测系统的重要一环。

本文的数字滤波算法依托吉林大学研制的浅地表电磁探测系统实现，系统的天线部分采用阵列式设计的方案，每组发射线圈对应多组接收线圈，可根据探测面积的大小增加或减少线圈组数。

1 数字滤波原理及其建模

图1 为系统控制单个模块的工作框图，采用FPGA + DSP + 计算机的模块化设计，每个模块采用FPGA + DSP的硬件架构实现对接收天线数据的采集与处理，通过网口与计算机完成通信，最终由上位机进行匹配滤波对噪声进行压制，提升所获信号的信噪比，完成目标物的识别与定位。

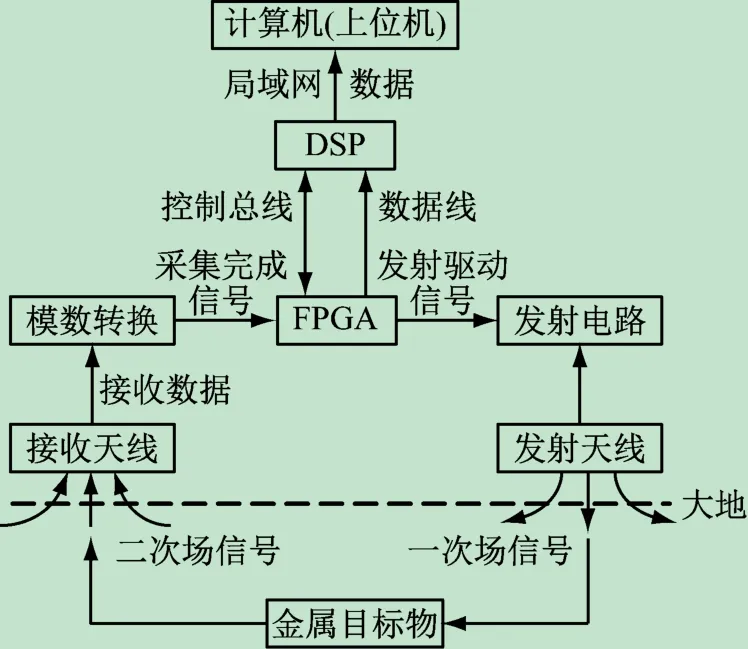
图1 单模块设计框图

1.1 匹配滤波的概念

匹配滤波是利用已知信号的特征进行检测的一种滤波方法。当滤波器的输入信号是某一类特定波形时，使输出信噪比达到最大的滤波方式即为匹配滤波。

在一个匹配滤波器中，设其线性输入信号由有用信号和噪声两部分构成，即：

式中：K为归一化常数。由式（3）可知，滤波函数h（t）是输入信号s（t）的镜像函数，匹配滤波过程就是信号相关的过程，滤波函数与目标函数的相似性越大，滤波效果越好，滤得信号的信噪比越高。

1.2 目标函数建模

本文中浅地表电磁探测系统车载工作，天线悬空放置于车辆前端进行电磁波的发射与接收，控制系统和计算机放置在车体内部。车辆行进时，整个系统实时探测，能够对当前位置处的金属目标物进行识别并报警。当车速为3 km／ h（0． 83 m／ s）时系统能够探测到深度50 cm以内，半径为15 cm，高8 cm的圆柱异常体。本文所采用的天线结构如图2 所示。由于天线为阵列式设计，可以根据探测宽度的需要增加接收线圈的组数和发射天线的面积。天线采用一发五收的设计，最外围是发射线圈，为了增大发射磁矩，发射线圈常用大电流设计，其面积也较大，内部的接收线圈采用八字型设计，以抵消一次场的干扰。接收线圈采用严格的对称式分布，位于发射线圈中心位置，每个接收线圈上下侧边缘位于发射线圈1 ／ 4 宽度处，采用平衡差动的方式接入电路［10-12］。当探测区域无金属目标物时，接收线圈感应的电动势为0。

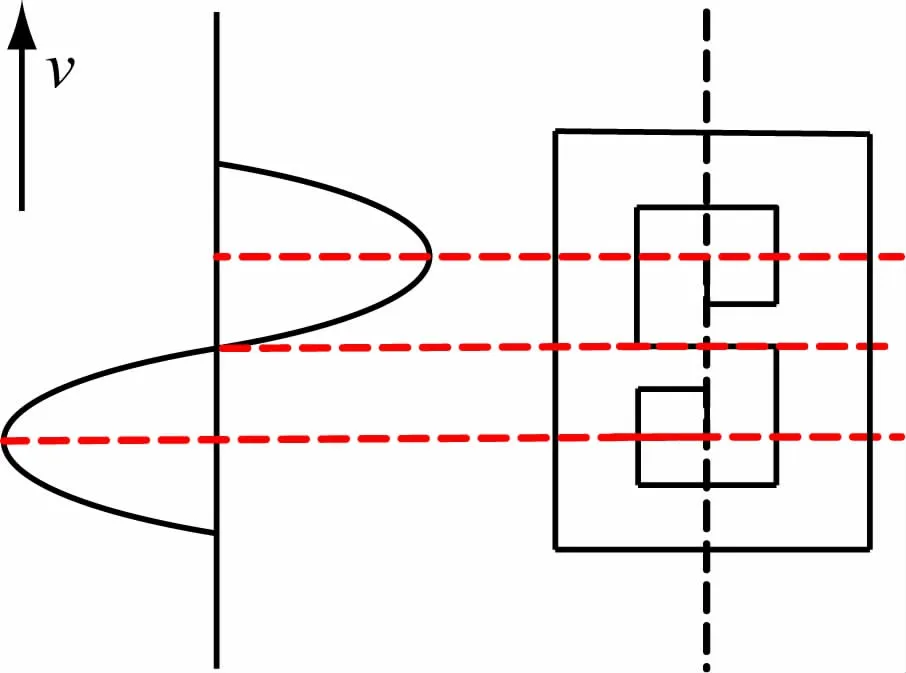
图2 探测天线示意图

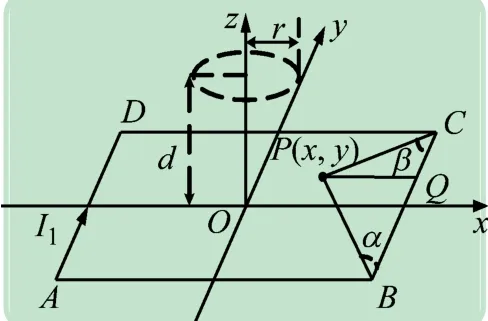
图3 天线磁场计算示意图

为了获得目标物在天线探测时的响应函数，从而获得良好的滤波函数，对天线周围的磁场分布进行分析。如图3 所示，以矩形发射线圈ABCD 的中心点O为坐标原点，构建空间坐标系。r为目标物与z轴距离（y坐标），d为目标物深度（z坐标）。

由于八字形线圈的结构可以抵消掉发射线圈发出的一次场，避免了一次场对接收线圈的干扰，所以本文不再对其进行计算，只考虑接收线圈周围出现金属目标物时其二次场的分布情况。在分析涡流形成的二次场时，把圆柱体金属目标物等效为半径b 的多组圆环体，等效之后的圆环体和发射线圈之间的距离是d，涡流是It。根据磁偶极子的磁通密度计算公式，可以得到：

式中，μ0为真空磁导率。同样深度情况下，天线正下方涡流It可近似认为相等。由式（4）可知，同一材料在同一深度激发的二次场强度与r的平方成正比。则由图2，当天线随车体以速度v经过金属目标上方时，接收线圈采集的二次场信号经模数转换后，将特征值按时间排列，会得到一条类似正弦的曲线。分析可得，目标波形的周期随天线运动速度变化而变化，速度越快，天线经过目标物的时间越短，目标波形周期越短。目标波形峰峰值受目标物金属含量和所埋深度有关，目标物金属含量越高，二次场越强，峰峰值越大；同一目标，距离天线位置越近，激发的二次场越强，峰峰值越大。

实验室环境下，单一背景探测所得的曲线也验证了这一结论。由图4 可知，采集数据在时间轴上排列呈正弦趋势。经计算，实验波形与正弦波有较好的相关性，又由于正弦波具有表达式简单，便于离散化的优点，可以提高数字滤波的计算速度，在处理大量数据时也不会影响系统的实时性，很好地满足了本系统对探测效率的要求。故本文采用正弦波作为滤波函数对所得信号进行匹配滤波。

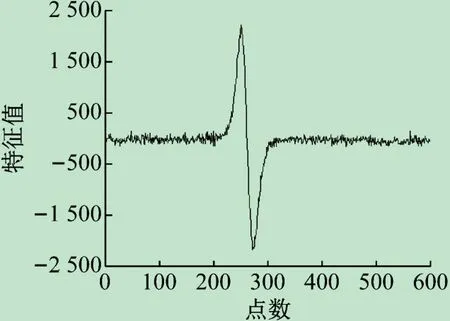
图4 单模块测试的特征分量曲线图

2 滤波器设计与实现

2.1 匹配滤波器的设计

匹配滤波算法流程如图5 所示。由于所采用的滤波函数为连续的正弦函数，而系统采集到的二次场信息为离散的点，需要对滤波函数离散化，进行取插值。对于系统采集到二次场数据，受实际条件限制，车体在行驶过程中不能始终保持理想的匀速状态，而采集到的数据按时间进行排列后，金属目标的响应波形其周期随速度快慢变化明显。而匹配滤波要求目标波形与滤波窗口函数有尽可能高的相似性［15］，而变化的目标函数显然与这一原则相违背。

图5 匹配滤波算法流程

为了削弱行进速度对目标波形的影响，对天线行进速度进行归一化处理，将滤波时横坐标的时间转化为天线的行进距离。按照距离排列的二次场信息，目标波形周期只与金属目标横截面积大小有关而与速度无关，由此消除速度对滤波效果的影响。获取距离信息的方法有两种：①读取时间信息的同时实时读取速度信息，两者进行积分，将时间转换为距离信息，以距离为横轴，特征值为纵轴对二次场特征值进行排列，进行匹配滤波；②增加硬件，在读取小车行进时间的同时，使用编码器对小车的行进距离进行记录，通过解码器直接读取距离信息进行滤波。由于第①种方法会增加算法的执行时间，且随着数据量的增加，严重拖慢滤波效率，而浅地表实际探测时需要在短时间内处理大量的数据信息，对系统的实时性有极高的要求。故采取第②种方法。

在探测过程中，由于天线行进快慢不同，可能导致速度较慢时，在一个位置处采得多组特征值的情况。此时，应对同一距离的多组特征值进行取平均，同时舍弃差异较大的个别特征值，消除随机误差。

将特征值取平均后，按照距离进行重新排列，记距离为x1，对应特征值y1，得到二次场特征值随距离分布的数组X( n )＝ ( xi，yi)( i ＝1，2，…，n )。设滤波函数的窗口宽度为d，即h（n）取d 个插值，则X（n）中每d个点为一组序列（第1 个点到第d个点为第一组序列，第2 个点到第d + 1 个点为第二组序列……），依次迭代，共有序列组数

将点x（1）对应距离记为y（1）距离，x（2）对应距离记为y（2）距离……x（m）对应距离记为与y（m）对应距离。将距离与其对应的滤波后特征值重新排列，可得到匹配滤波后数组

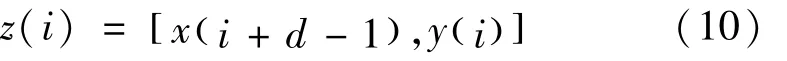
和滤波前序列X（n）相比，z（n）少了d - 1 个点。在实际探测中，本文所使用的编码器每0． 03 m上报一次距离信息给上位机。因此滤波后的序列坐标原点对应实际行进距离的坐标

故在实际探测过程中，需以探测天线行进δ 处为距离坐标的原点。在工程应用中，根据实时性的要求，一般所取窗口宽度在200 ～300 范围内，对应空采距离为6～9 m，并不影响实际探测效率和结果。

2.2 目标识别与定位

为对目标物进行进一步的识别与定位，需要对式（10）的z（i）进一步处理。经实验室环境验证，本文所使用目标物在50 cm 处响应特征值约为1 000。设置目标物判别阈值P ＝400。若有多个连续点（5 个及以上）对应z（i）大于P，则认为此处存在金属目标。

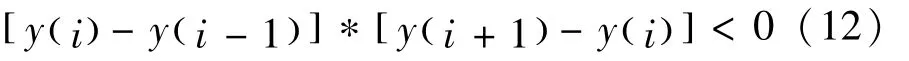
由于匹配滤波可以消除随机误差的干扰，所以可以认为z（i）序列中没有随机误差。此时，若z（i）满足y（i）＞400 且则认为该点是极值点，对应坐标为该目标物中心位置，记录此时距离信息，上位机进行报警，并上报此时距离信息与天线所在位置编号，完成目标物定位。

3 实验验证

在实验室环境下进行匹配滤波效果的实验验证，实验中采用半径15 cm，高5 cm的圆柱体金属，埋藏在地表下距离天线20 cm的位置。使车载天线向前匀速运动，经过金属目标正上方。将得到的数据按照距离排列，如图6 所示。由于数据量较大，选取其部分进行分析。

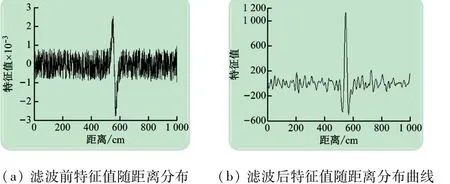
图6 滤波前后数据对比

分析数据可知，滤波前的目标信号波形较粗糙，毛刺明显，且本底噪声干扰严重，整体信噪比较低。经匹配滤波后，对本底噪声压制作用明显，目标波形从类正弦信号变成一个主瓣两个旁瓣的目标信号，且目标信号能量最大的中心点与滤波前保持一致，不影响滤波前后的位置判决。整个波形的信噪比得到了明显提升，印证了匹配滤波对信噪比的提升作用。