F=1自旋相干态在外场中的量子演化
2020-09-14师春娟张杰
师春娟,张杰
(太原理工大学 物理与光电工程学院,山西 太原 030024)
0 引言
自旋相干态(spin-coherent-state) 的演化首先是在赝自旋F=1/2多粒子系统中[1]提出的,其中3个自旋正交算符属于SU(2)群,并满足对易关系[Jx,Jy]=iћJz。近年来,越来越多的目光集中于自旋压缩态和多粒子量子纠缠态的制备[2],这些都是由自旋相干态在非线性效应的驱动下演化而来。特别是自旋压缩态,已经在量子信息[3]、量子模拟[4-5]、 高精度测量[6-7]以及原子干涉仪[8]等方面显示出广泛的应用前景,一些实验已经在如何实现自旋压缩态方面取得成功[9-10]。
F=1旋量玻色爱因斯坦凝聚体(BEC)又称为3能级系统,由于其具有内部自旋自由度,且已经在光阱[11]中实现,经常被看作是制备压缩态和纠缠态[12]的最佳选择。这个多粒子系统的数学结构可以用SU(3)群描述,并表现出复杂的量子磁序[9-13],而传统的自旋角动量空间{Jx,Jy,Jz}只是SU(3)群空间的一个子空间,换句话说,系统中的物理量除了传统的自旋角动量算符外,还有所谓的四极矩算符,并可以表述成一组3×3的矩阵,二者的组合将引入更多自由度和新物理量。在赝自旋F=1/2多粒子系统中,只有传统的自旋角动量空间{Jx,Jy,Jz},且任意泡利矩阵的平方是单位矩阵,任意两个不同泡利矩阵的反对易关系为0。而在自旋F=1系统中,任意自旋矩阵的平方不再是单位矩阵,而是对应的四极矩张量矩阵。另外,我们不难注意到,自旋F=1/2系统在Fock态|n1,n2〉(又称Dicke态)表象中有如下关系:
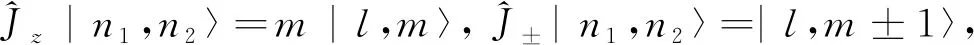
(1)

1 SU(3)结构
为了更好地理解自旋F=1系统的性质,我们首先引入SU(3)群的概念。自旋F=1的单粒子密度矩阵可分为单极、偶极和四极矩[9],具体可以分为3个偶极(角动量)算符Jμ(μ=x,y,z),在自旋z轴表象中表示为一些3×3的矩阵
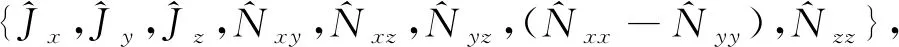
(2)
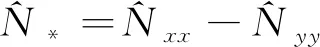
(3)
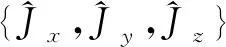
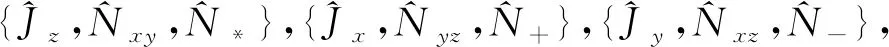
(4)
2 非线性哈密顿量和自旋相干态
2.1 非线性哈密顿量
外场中自旋F=1玻色凝聚体的哈密顿量二次量子化形式可写成对称部分和反对称部分以及偶极-偶极相互作用三项之和[14-15]H=HS+HA+HD:
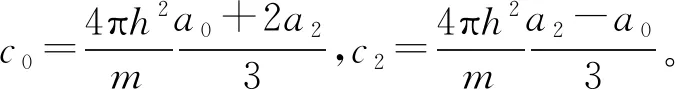
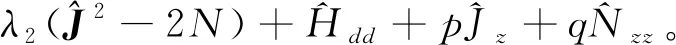
(5)
自旋角动量算符满足如下关系:

(6)

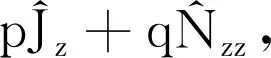
(7)
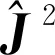

(8)
2.2 自旋相干态在粒子数表象中的表示
自旋相干态(简称CSS) 指的是具有内部自旋自由度的粒子在初始时刻的自旋状态完全一致,并且随着时间增长,所有粒子的状态始终保持一致地变化。我已经知道,不考虑内部自由度的N个全同玻色子构成的标量BEC可以描述成Fock态的形式,如
而如果要考虑内部自由度,我们只需要将上述表达式做如下扩展:
(9)

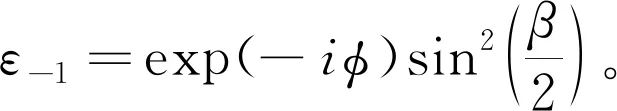
(10)
由于自旋相干态中各粒子之间不存在关联,我们可以直积N次以获得足够多的粒子数。在自旋F=1系统中,粒子数占据态(Fock态)表述为|n1,n0,n-1〉三组分的形式,因此F=1自旋相干态可以表示为

(11)

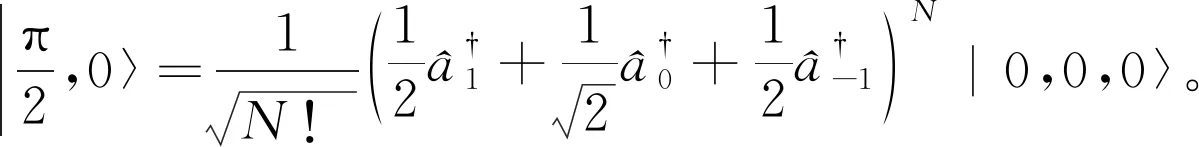
(12)
它由一系列三分量Fock态|n1,n0,n-1〉叠加而成[18-19],如果令
n1-n-1=m,η=n1+n-1=N-n0,
可以将Fock态改写成类Dicke态模式:

(13)
而在两分量F=1/2赝自旋系统中,自旋相干态表示为

(14)
我们可以看到,其中的m=0分量是区别于F=1/2和F=1系统的关键因素。
自旋F=1角动量升降算符满足:

(15)
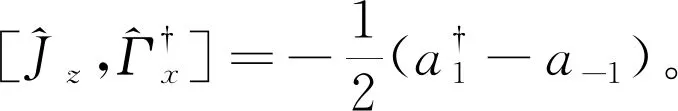
(16)

(17)
事实上,真正角动量本征态也是一系列Fock态的叠加,可以写成
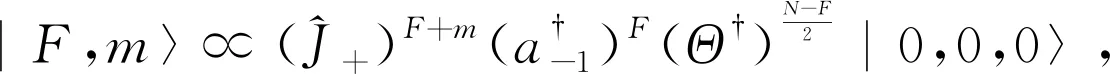
(18)
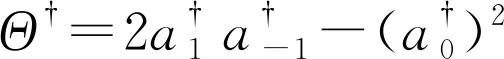
3 结果与讨论
在这一部分我们讨论外场中一阶和二阶塞曼效应对自旋相干态动力学的影响,并计算总自旋期望值(属于一阶关联)和压缩系数(二阶关联)的演化。
3.1 没有外磁场时的演化


(19)
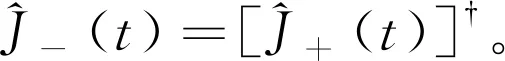
(20)
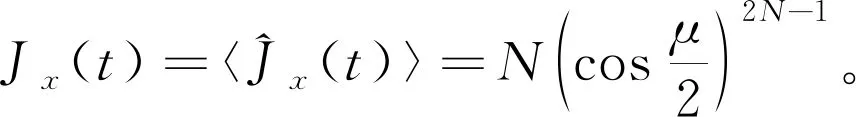
(21)

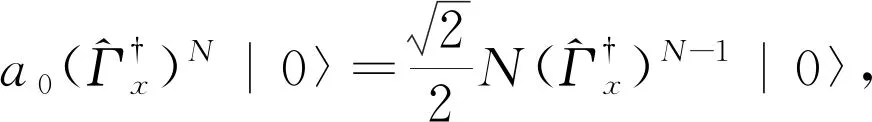
(22)
详见附录B。压缩系数是刻画非线性效应的重要参数,其定义为:

(23)

其中:

(24)
这一结果同样与数值计算结果完全一致。我们的解析结果可以很好地用来研究压缩率和粒子数的关系,如图1(c)所示。严格对角化数值计算的矩阵规模会随粒子数而指数增长,显然我们的解析结果在研究大粒子数情况有独特优势。

图1 (a)平均自旋的演化; (b)自旋压缩参数ξ2的演化,总粒子数N=20,黑色实线和红色虚线分别表示解析结果和数值结果;(c)压缩随总粒子数的变化关系Fig.1 (a) (Color online) The evolution of the average spin (b) the spin-squeezing parameter ξ2 with total particle numbers N=20.The black solid line and the red dashed line denote the analytical and numerical results respectively;(c) the dependence of spin-squeezing parameter ξ2 on the total number N.
3.2 受外磁场影响的相干态的演化
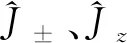
如果磁场受到弱磁场作用影响,塞曼分裂是线性的,二阶塞曼效应可以略去,有效哈密顿量为

(25)
初始总自旋的演化为

(26)

图2 (a)平均自旋的演化;(b)自旋压缩参数ξ2的演化,总粒子数N=20,黑色短虚线和粉色实线分别表示p=0、p=30的结果Fig.2 (a) (Color online) The evolution of the average spin the spin-squeezing parameter ξ2with total particle numbers N=20.The black short-dashed line and the orange solid line denote the p=0 and p=30 results, respectively.
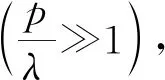
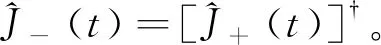
(27)
我们计算出二阶关联:
发现压缩系数也被调制,如图2(b)所示。其中
a1=1-(cosμ)2N-2(cos2α),
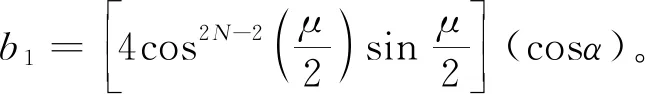
(28)
(29)
当考虑微波驱动交流塞曼效应时,二阶塞曼效应参数q的正负号可以通过红蓝失谐来改变。这对于调节自旋相干态给出了重要手段,我们首先考虑二阶塞曼项占主导情况:
(30)

图3 (a)平均自旋的演化; (b)自旋压缩参数ξ2的演化,总粒子数N=20,黑色短虚线和红色实线分别表示q=0和q=30的结果; (c)展示的是压缩演化的细节图Fig.3 (a) (Color online) The evolution of the average spin (b) the spin-squeezing parameter ξ2 with total particle numbers N=20,The black short-dashed line and the red solid line denote the q=0 and q=30 results,respectively;(c) the details of spin-squeezing parameter ξ2.
平均自旋演化为

(31)
[(N-1)(1+cos(2μ-2q)+(cosμ)2)]+
C=A+N。
(32)

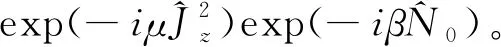
(33)
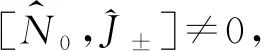
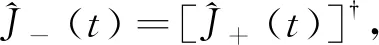
(34)
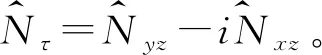
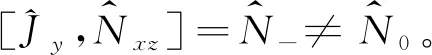
(35)
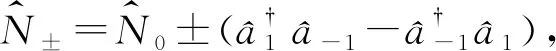

(36)


(37)
初态演化是

图4 (a) 平均自旋的演化;(b)自旋压缩参数ξ2的演化,总粒子数N=20,黑色短虚线和紫色实线分别表示p=q=0和p=q=30Fig.4 (a) (Color online) The evolution of the average spin (b) the spin-squeezing parameter ξ2 with total particle numbers N=20.The black short-dashed line and the red solid line denote the p=q=0 and p=q=30 results, respectively

(38)
[1+cos(2μ+2q)]-(1+cosq))+(cosμ)2N-2cosq],
C=A+N。
(39)
角动量升降算符演化成
4 结论
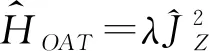
附录ASU(2)子空间和对易关系
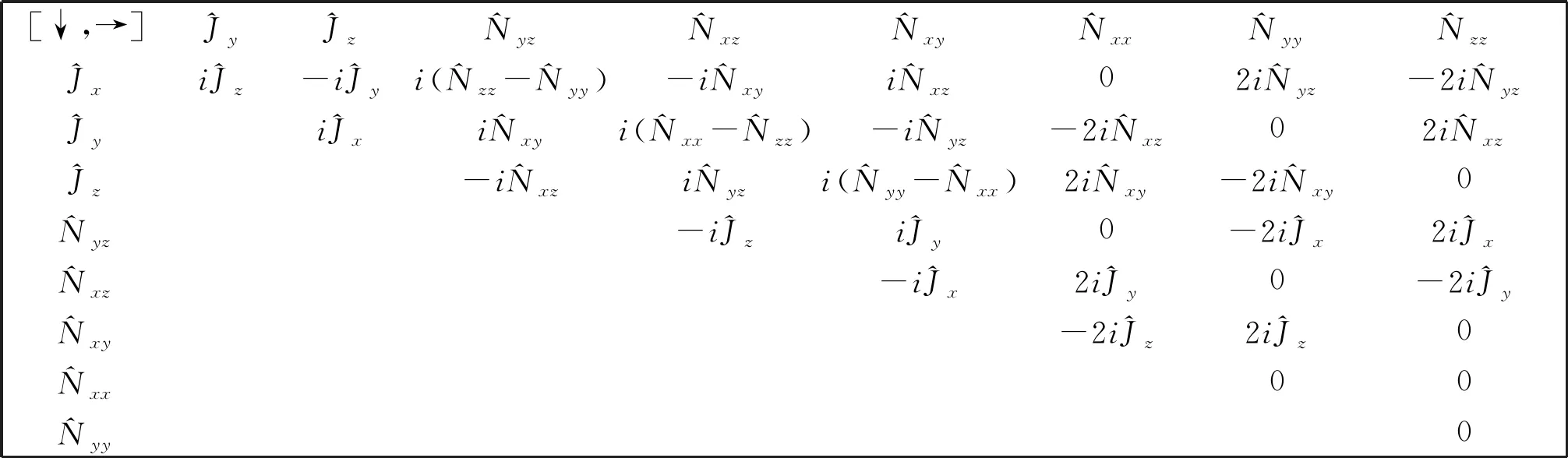
[↓,→]^Jy^Jz^Nyz^Nxz^Nxy^Nxx^Nyy^Nzz^Jxi^Jz-i^Jyi(^Nzz-^Nyy)-i^Nxyi^Nxz02i^Nyz-2i^Nyz^Jyi^Jxi^Nxyi(^Nxx-^Nzz)-i^Nyz-2i^Nxz02i^Nxz^Jz-i^Nxzi^Nyzi(^Nyy-^Nxx)2i^Nxy-2i^Nxy0 ^Nyz-i^Jzi^Jy0-2i^Jx2i^Jx ^Nxz-i^Jx2i^Jy0-2i^Jy ^Nxy-2i^Jz2i^Jz0 ^Nxx00 ^Nyy0
附录B相干态动力学演化在粒子数表象中的计算
三分量Fock的初始自旋相干态可以基于Fock态|n1,n0,n-1〉表示为
|n1,n0,n-1〉。
(A1)
自旋系统的基本演化是

(A2)
(A3)

我们得到以下公式:
(A4)
或
(A5)
此时有:
(A6)
为了计算期望值,我们需要向右移动湮灭算符,向左移动产生算符,
(A7)
(A8)
