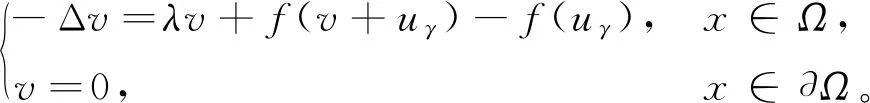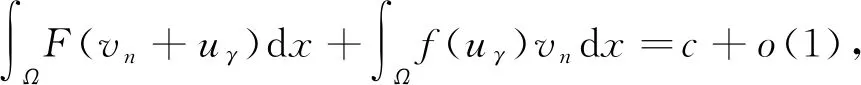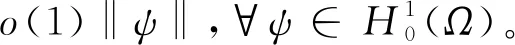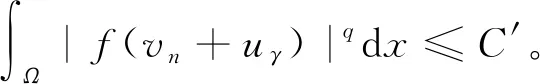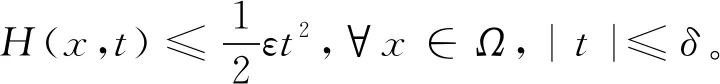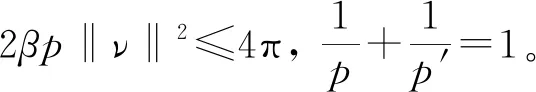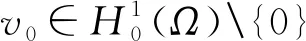R2中半线性椭圆型方程多解的存在性
2020-09-14张亚静李巧琴庞璐
张亚静,李巧琴,庞璐
(山西大学 数学科学学院,山西 太原 030006)
0 引言
我们研究以下半线性椭圆型方程:

(1)
其中Ω是R2中一个光滑有界区域,g∈C0(Ω)是一个非负且不恒为零的函数,λ≥0,γ≥0,函数f满足次临界增长条件。f在+∞处满足次临界增长条件是指对一切β>0都成立
f在-∞处满足次临界增长条件可类似定义。
近年来,很多人研究与问题(1)相关的方程:
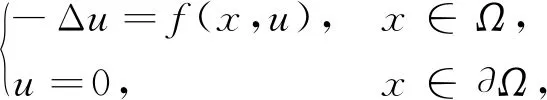
(2)

当空间维数N≥3时,具有物理与几何背景的方程

(3)
自从20世纪80年代以来得到了广泛研究。Brezis和Nirenerg在他们著名的论文[11]中指出该问题解的存在性不仅依赖于λ,而且与空间维数N有密切关系。邓引斌[12]以及朱熹平等人[13]研究了下面的非齐次问题

(4)
受到以上研究工作的启发,我们研究问题(P)γ。设函数f满足:
(H1)f∈C1(R,R),f(0)=f′(0)=0,f(t)t≥0,∀t∈R;
(H2)f(t)-f(s)>f′(s)(t-s),∀0≤s (H3)存在独立于f的常数α>1,使得αf(t)≤f′(t)t,∀t≥0; 这些假设条件相对比较简单, 比如(H3)是著名的Ambrosetti-Rabinowitz类型的条件,(H4)也是很常见的条件。 则称u是问题(P)γ的一个解。 我们获得如下的结果。 定理1 假设函数f在±∞处满足次临界增长条件。对任意的λ∈(0,λ1),存在一个正数γ*使得当γ∈(0,γ*)时,问题(P)γ存在一个正极小解(极小解的定义将在第1节给出);当γ∈(γ*,+∞)时,问题(P)γ不存在正解。 定理2 假设函数f在±∞处满足次临界增长条件。对任意的λ∈(0,λ1),γ∈(0,γ*)(即定理1中的γ*),问题(P)γ至少存在两个解。 本节将使用单调迭代法证明第一个解的存在性。 由于函数f具有次临界增长,故存在常数C和β使得 |f(t)|≤Ceβt2,∀t∈R。 证明由条件(H4)可知存在常数C>0使得 再由条件(H3)可知 (α+1)F(t)≤f(t)t, ∀t≥0。 因此 取C1=-mint≥0[f(t)-(λ1-λ)t],我们可得 f(t)≥[λ1-λ]t-C1, ∀t≥0。 (5) 于是 因此 由(5)式可得 故 引理2 对任意λ∈[0,λ1),当γ充分小时, (P)γ至少存在一个正解。 证明既然f′(0)=0,那么存在ε>0使得 f(εφ1(x))<[λ1-λ]εφ1(x), ∀x∈Ω。 令 (6) (7) 由(6)可得 (8) 类似地,由(7)可得 (9) 从(8)中减去(9)并且令ψ=(u1-w1)+,我们得到 因此ψ=0,于是u1≤w1在Ω上几乎处处成立。 类似地,由上、下解的定义以及(6)和(7),我们可以证明u0≤u1且w1≤w0。 我们接着使用归纳法来证明:un≤un+1≤wn+1≤wna.e.x∈Ω,∀n=0,1,2,…当n=0时上式显然成立。归纳假设 un-1≤un≤wn≤wn-1a.e.x∈Ω。 由(6)和(7)可得 (10) (11) 因此un+1≤wn+1a.e.x∈Ω。 类似地我们可以证明un≤un+1以及wn+1≤wn。 由前面的两个结论可知 令 显然,u(x)≤w(x)a.e.x∈Ω。在(10)中取ψ=un+1可得 在(10)中令n→∞可得 类似地可知w也是(P)γ的一个弱解。然而,我们并不知道二者是否是两个不同的解。 un≤U≤wn, ∀n。 令n→∞可得 u≤U≤w, (ii)当γ充分小时,引理2所得到的解实际上是(P)γ所有正解中的一个极小解。 引理3 对λ∈[0,λ1),存在正常数γ*使得当γ∈(0,γ*)时,(P)γ至少存在一个正解;而当γ>γ*时,(P)γ无正解。 证明令 (P)γ都存在至少一个正解}。 由引理1和引理2可知γ*的定义是合理的。 任意取定γ0∈(0,γ*),我们取δ>0使得γ0+δ<γ*,设uγ0+δ是(P)γ0+δ的一个解。易知0是(P)γ0的一个下解并且uγ0+δ是一个上解。运用与引理2证明过程同样的方法可以得到(P)γ0的一个解uγ0,由注1可知uγ0是一个极小解。 再由类似的方法可知当γ>γ*时,(P)γ无正解。 引理4 假设λ∈[0,λ1),γ∈(0,γ*),其中γ*在引理3中定义。再设uγ是(P)γ的极小解,则 (12) 可以达到且τ>1。 因此|ψn|2是有界的。既然 因此当n→∞时, 由Lebesgue控制收敛定理可得 因此ψ0达到τ。显然|ψ0|也可以达到τ,所以不妨假设ψ0≥0,x∈Ω, 由Lagrange乘子法可知 (13) (14) 由(13)和(14)可得 因此τ>1。 引理5 其中, S={uγ|γ∈(0,γ*)},uγ是(P)γ的一个极小解。 证明对任意uγ∈S,由引理4可知 于是 (15) 显然 (16) 由(15),(16)以及条件(H3)可知 既然 我们得到 此处δ>0充分小且满足 因此存在仅依赖于λ1,λ,α,γ以及g的正常数C2使得 (17) 由(16)和(17)可得 因此存在独立于γ的正常数C使得 ‖uγ‖≤C。 (18) 现在我们证明定理1。 假设γjγ*且uγj∈S,由引理5可知存在一个序列,不失一般性,仍记为{uγj},使得在中uγj弱收敛于u*,在L2(Ω)中uγj→u*,uγj(x)→u*(x)a.e.x∈Ω,易知u*是(P)γ*的一个解。对任意γ≥0,0都是(P)γ的一个下解。因此我们可以使用单调迭代法获得一个极小解。 我们引入下面的问题 (19) 为了获得(P)γ的第二个解只需证明(19)存在一个非平凡解。这样uγ+v就是(P)γ的第二个解。 引理6 假设f具有次临界增长,那么J满足Palsis-Smale条件。 (20) (21) 由条件(H1)和(H4)可知对任意ε>0都存在tε>0使得 F(t)≤εf(t)t, ∀|t|≥tε。 (22) 既然f具有次临界增长,故 |f(t)|≤Ceβt2, ∀t∈R。 (23) 由(20)和(21)可知 (24) 在(21)中取ψ=vn+uγ可得 o(1)‖vn+uγ‖= (25) 将上面的不等式代入(24)可得 c+o(1)≤Cε‖νn‖+C。 既然 (26) 利用(23)以及和文献[16]中(3.9)相同的原因,我们可得存在q>1以及常数C′使得 (27) (21)减去(26)并且令ψ=vn-v可得 o(1)‖vn-v‖。 既然 |f(vn+uγ)-f(v+uγ)|q|vn-v|q′≤ 2C′|vn-v|q′→0, 可得 令 h(x,t)=f(t+uγ(x))-f(uγ(x))-f′(uγ(x))t, 则 引理7 对λ∈[0,λ1),γ∈[0,γ*),问题(19)存在非平凡解。 证明我们首先表明存在η>0,ρ>0使得对‖ν‖=η,成立 J(v)≥J(0)+ρ。 (28) 由中值定理可得 h(x,t)=f(t+uγ)-f(uγ)-f′(uγ)t= f′(uγ+θt)t-f′(uγ)t, (0<θ<1), 于是,存在δ>0使得 (29) 由(23)可得对q>2,成立 H(x,t)≤Ce2βt2|t|q,∀x∈Ω,|t|≥δ。 (30) 由(29)和(30)可得 (31) 于是,由Trudinger-Moser不等式可得 J(v)-J(0)= 因此如果我们取‖ν‖=η充分小,则(28)成立。 (32) 由条件(H1)和(H4)可知存在常数C3>0使得 于是,存在正常数C4和C5使得 F(t)≥C4|t|p-C5, ∀t∈R。 因此 这样我们就验证了(32)成立。 应用山路定理(参见文献[17]中定理4.8.5)引理得证。 由引理7立刻证明了定理2。

1 第一个解的存在性

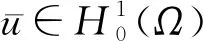
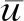

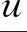

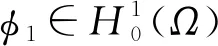

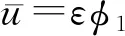
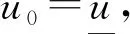
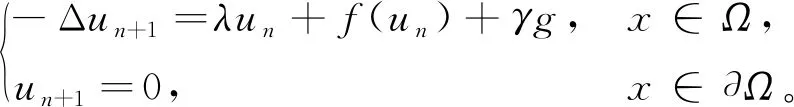










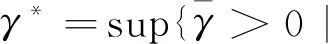
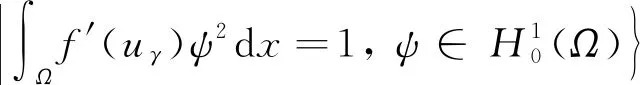






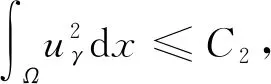
2 第二个解的存在性