注采连通关系计算方法的改进及在配注中的应用
2020-09-14石国伟蓝海刚吉兰敏
贾 鹿,石国伟,石 峰,蓝海刚,吉兰敏
(1.中国石油新疆油田分公司,新疆 克拉玛依 834000;2.哈里伯顿北京奥伯特石油科技有限公司,北京 100084)
0 引 言
注水开发油田注采调配方案的制订多以人工分析为主,对于油水井注采连通关系和见效比例等关键信息多采用经验给定或平均分配等方式进行简化处理,调配方案的制订缺乏客观科学的依据,实施效果不理想。为解决该问题,需要建立一种行之有效的注采连通关系量化分析方法。常用的井组注采连通关系分析方法主要有同位素载体法、注水井吸水剖面、井间示踪剂测试、干扰试井、生产测井等现场测试方法,这些方法的施工影响生产,成本较高,且不能量化表征油水井之间的连通关系[1]。一些学者利用地质资料、生产动态数据和生产测试资料,从动态和静态角度对井组注采连通状况进行了半定量评价[2-9];另一部分学者则尝试采用决策树、数值模拟等方法来判断注采连通关系,实现了定量或半定量的评价,但自动化程度不够,现场可操作性差[10-15]。相关学者也对此进行了大量研究,采用数学方法量化表征注采连通关系。Heffer[16]使用Spearman秩相关系数,通过油藏流体的流动方向及主应力方向,判断井间连通性,但该方法基于注采井平均分布的假设,且不能给出注采连通关系的量化结果;Pandar[17]等使用神经网络计算注采井间的连通性,该方法需要一定的数据量和不断的训练才能得到合理的结果,数据的获取和效率制约了该方法的应用;Yousef[18]使用较为复杂的容积模型进行关联系数的求解,模型建立和求解过程非常繁琐,不易于推广。Albertino[19]使用多元非线性回归方法,仅基于油水井月生产数据和相关流体物性参数即可量化表征注采井间连通关系,方法便捷,可操作性强,在一定程度上满足了油田配注的需求。但该多元线性回归方法没有考虑井底流压变化的影响,因此,该模型在实际应用中仍然存在一些缺陷。针对上述问题,对现有的注采连通关系分析方法进行了融合与改进,提出了一种考虑井底流压变化的多元线性回归注采连通关系分析模型,并将注采连通分析模型与井组配注模型相结合,可快速计算出每个井组中注水井的配注量。
1 注采连通关系定量分析模型
1.1 多元线性注采连通模型原理
无限大油藏中某一点由于注水井注入速度引起的压力变化[1]可以表示为:
(1)
d=1/η
(2)
式中:Δp为与注水井距离为r处受注水影响的压力变化,MPa;C1为与产液量和地层流体物性相关的系数,MPa;Ei为幂积分函数;r为从该点到井的距离,m;t为时间,s;η为导压系数,即压力波向周围传播的速度,cm2/s。
油井产能采用PI方法表示:
(3)

假设井底流压不变,考虑注水数据的离散性,使用叠加原则,某一时间的井底压力变化Δp(t)引起与注水井距离为r处的油井的产量变化计算公式为:

(4)
将注水井的一个波动视为一个注入刺激,则一口油井的产出是受多口注水井刺激的结果[1]:

(5)
(6)

1.2 多元线性注采连通模型的改进
可以发现,上述模型的假定条件是油井井底流压不变,但实际生产过程中井底流压往往是变化的。因此,需要在此基础上对模型进行改进,考虑油井井底流压变化,使之更符合实际生产规律。
假设只有1口注水井和1口油井的油藏,地层压力和注入量及产液量关系如下[18]:
(7)
式中:ct为综合压缩系数,1/MPa;Vp为孔隙体积,m3。
将式(7)和式(3)进行联立,可得[18]:
(8)
(9)
式中:τ为与供给面积有关的时间常数。
对式(8)进行求解,可得:
(10)
式中:ξ和ζ为积分变量。
对于多口油井多口注水井的油藏[18],则有:
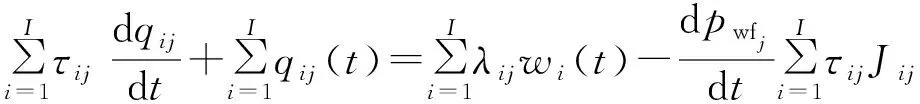
(11)
式中:qij为油井j受注水井i影响的产液量,m3/d;τij为注水井i对油井j的供给面积时间常数;Jij为注水井i对油井j采液指数的影响值,m3/(d·MPa)。
对式(11)进行求解,并进行简化,可获得连通关系模型:
(12)
考虑注采不平衡以及注水井刺激发出和油井接收之间的时间延迟作用,模型转化为:
(13)
一个时间点数据可以建立一个方程,多个时间点数据即可建立方程组:
(14)
式中:M为时间点数据的个数。
当M≥I时,方程有解,此时式(14)为超定方程组,采用最小二乘法进行求解,获得方程中的各个系数(λ1j,λ2j…λIj),即为油水井之间的连通系数,代表了每口注水井对油井j的影响。每口油井均对应一个方程组,N口油井对应N个方程组,以油井j为例,方程组如下:
(15)
式中:αw1w2为各月第1口注水井的平均日注水量与第2口注水井的平均日注水量的乘积之和,(m3/d)2;αw1pj为各月第1口注水井的平均日注水量与油井j的井底流压的乘积之和,MPa·m3/d;αw1qj为各月第1口注水井的平均日注水量与油井j的平均日产液量的乘积之和,(m3/d)2;αpjqj为各月油井j的井底流压与油井j的平均日产液量的乘积之和,MPa·m3/d。
2 井组配注计算模型
将多元线性注采连通分析模型与井组配注模型进行整合,解决油田注采调配设计的效率和准确性的问题,对于实现油田智能调配具有十分重要的意义。
井组配注模型利用油井月度生产数据、流体物性参数、油水井连通系数(油井受注水井影响系数),结合井组的注采比要求,即可批量计算区域的注水井配注结果。其计算模型为:
Gi(t)=[V1(t)λi1+…+Vj(t)λij+…VN(t)λiN]IRRi
(16)
(17)
式中:Gi(t)为以注水井为中心的i井组的配注量,m3/d;Vj(t)为某一时间油井j的采出液地下体积,m3/d;IRRi为i井组的设计注采比;qoj(t)为油井j日产油量,t/d;Boj为油井j地下原油体积系数,m3/m3;ρj为油井j地面原油密度,g/cm3;qwj(t)为油井j日产水量,m3/d。
3 现场应用
3.1 注采连通模型的应用与验证
以新疆油田某区块为例,来介绍改进型注采连通分析模型的应用。该区块生产层位为克下组,是一个被断裂切割的封闭断块油藏,构造为东南倾的单斜,顺倾斜方向逐渐变陡,地层倾角为3~30 °,为山麓洪积相。油藏中部埋深为1 160 m,油藏温度为40 ℃。平面上各区物性差异比较大,孔隙度为16.6%~18.7%,渗透率为59.4~805.4 mD,地层原油压缩系数为1.327×10-3MPa-1,地面原油密度为0.857 g/cm3,原油体积系数为1.18 m3/m3,水体积系数为1.0 m3/m3,地层水水型为NaHCO3,采油井为125口,注水井为88口,整体采用五点法井网布井。
3.1.1 模型性能验证
从该区块生产油井中随机筛选20口生产油井,分别采用改进前与改进后的线性注采连通模型对2014年至2018年的实际生产数据进行拟合,并利用决定系数(R2)来评价2种模型的性能(表1)。由表1可知,注采连通模型经改进后,大部分井决定系数显著提高,改进前模型的R2的平均值为0.827 3,改进后模型的R2的平均值为0.863 4。
3.1.2 计算结果验证
分别利用原模型和改进型多元线性注采连通分析模型计算该区块的注采连通系数(即油井受周边注水井的影响系数)(表2)。为了判断2个模型计算结果的准确性,利用井间示踪剂测试结果作为评判依据。
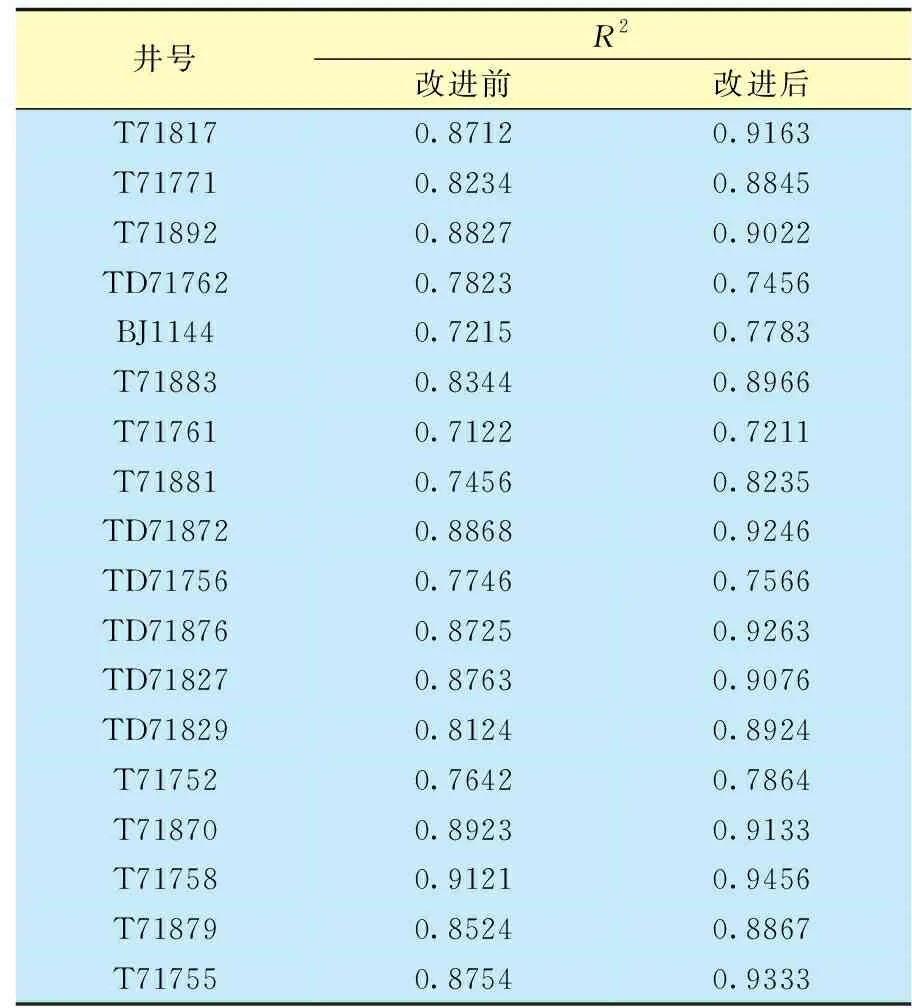
表1 多元线性注采连通模型决定系数对比Table 1 Comparison of decision coefficients for multiple linearinjection-production connectivity model
示踪剂测试可提供某一注水井注入示踪剂后的见剂油井、突破速度等信息。因此,首先可对受注水井影响的油井井数进行验证。对该区块的12个井组统计示踪剂见效情况:一线见效井为27口,二线见效井为4口。原模型的分析结果为:一线见效井为21口,二线见效井为2口,一线见效井符合率为77.8%;改进模型分析结果为:一线见效井为25口,二线见效井为8口,一线见效井符合率达到92.6%。
另外,示踪剂的突破速度可近似反映油井受周边注水井的影响系数(连通系数),可通过对比优势方向和非优势方向的符合率来验证改进模型计算的连通系数的准确性。以油井TD71722为例,示踪剂测试结果表明,该井受4口注水井影响,优势方向为T71330、TD71421井,突破速度分别为26.0、13.8 m/d,改进模型计算的连通系数对应为51.42%和30.20%,两者结果基本一致;而原模型分析结果显示优势方向为T71330、T71424井,与实测结果存在一定偏差(图1)。从表2中的几组计算结果来看,改进模型与示踪剂测试结果的符合程度更高。
利用改进模型计算该区块的所有井组的连通系数,结果显示:区块边部多为单向见效,中部多为多向见效;单向见效井为51口,双向见效井为47口,多向见效井为11口,双向与多向见效井比例为53.2%。分析结果与油田地质研究及动态分析相符,进一步从宏观层面验证了该模型的适用性。
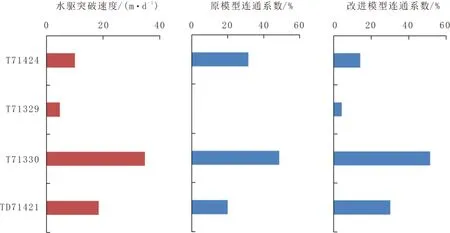
图1 TD71722井连通系数与水驱突破速度对比
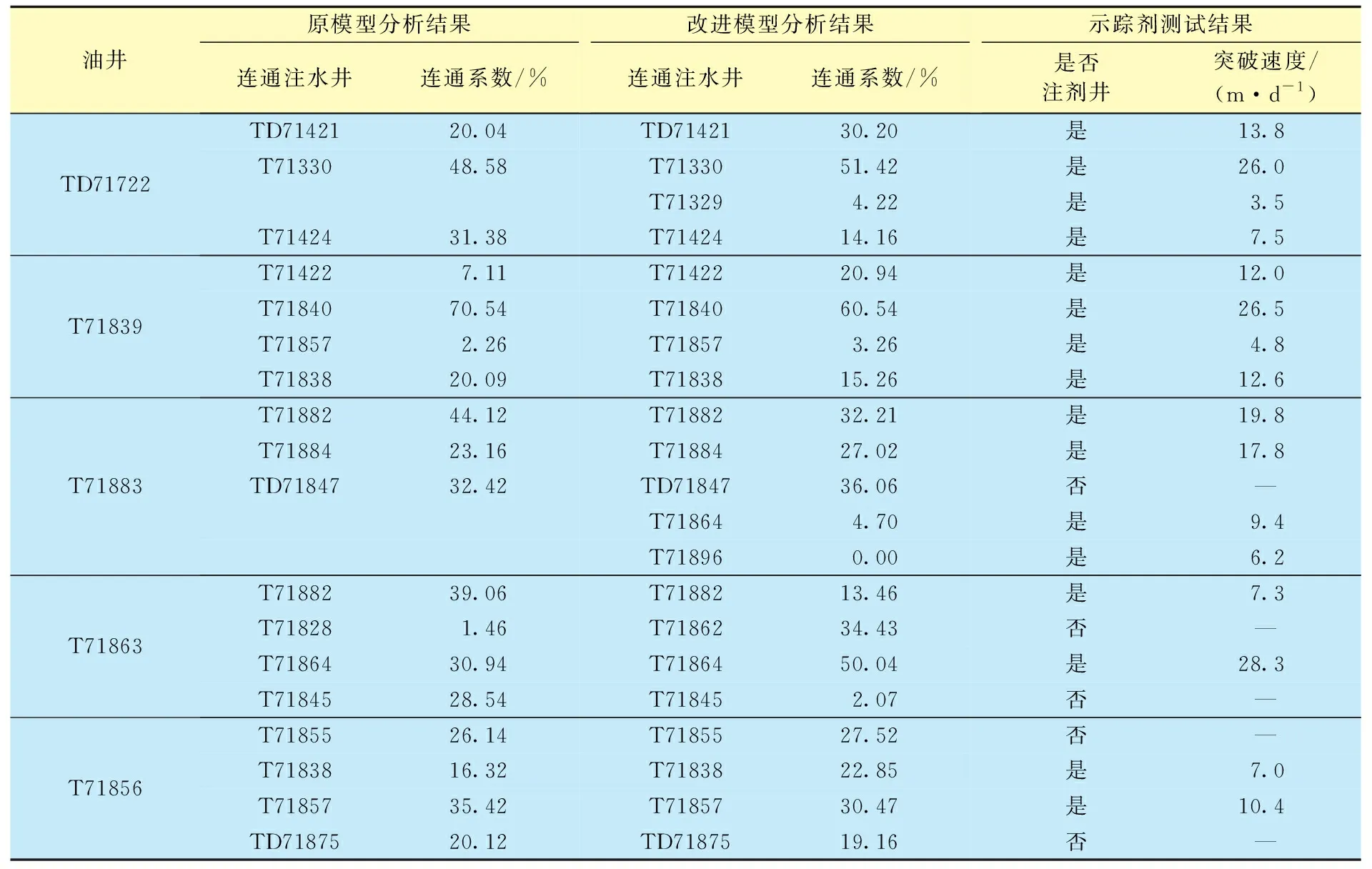
表2 新疆油田某区块注采连通系数计算结果与示踪剂结果Table 2 Injection-production connectivity coefficients and tracer monitoring data of a block in Xinjiang Oilfield
3.2 井组配注计算模型的应用
基于改进模型注采连通系数分析结果,再利用井组配注计算模型即可批量计算各井组配注量(表3),并可在此基础上汇总出区块的配注量。部分井组的配注结果见表2。注采连通分析模型和井组配注模型的应用大幅提高了现场配注工作的效率和准确性,使得注水工作“季配月调”成为现实,实际应用中也取得了较好的生产效果。2019年在试验区共计指导调配216井次,区块整体含水上升率由2018年的4.6%降至3.2%,自然递减率由10.9%降至8.1%,对于该区控水稳油工作发挥了较为积极作用。通过及时合理的调配工作,全区有15个井组取得了降水增油的效果,47个井组含水上升速度减缓。较为典型的井组如T71882井组,该井组主要产层为克下组的S72-3、S73-2、S73-3和S74-1层,其中,S73-3层为主要吸水和产液层,S74-1层为低产层,井间连通性较好,示踪剂测试结果显示周边主要有5口见效井。调配前井组日配注量为38 m3/d,日产液量为64.01 t/d,日产油量为7.26 t/d,综合含水为88.7%,平均动液面为802 m;利用改进模型分析,该井组配注量为30 m3/d即能满足地层均衡注采的需求,下调注水量后20 d左右开始见效,井组地层能量和产液量保持较好,降水增油现象明显,初期日产液量为62.88 t/d,平均动液面为814 m,综合含水下降为85.2%,日产油量上升为9.34 t/d。注水井T71882井的吸水剖面也有一定程度的改善,高渗层S73-3层的吸水比下降,由49.18%降至42.60%,潜力层S72-3和S73-2层吸水比提高,分别由22.54%和24.18%上升至26.42%和28.38%;受此影响,井组中各油井含水率均有明显下降,其中,2口高含水井T71883、TD71303井最为明显,含水分别由97.3%和92.3%下降至94.2%和87.6%。
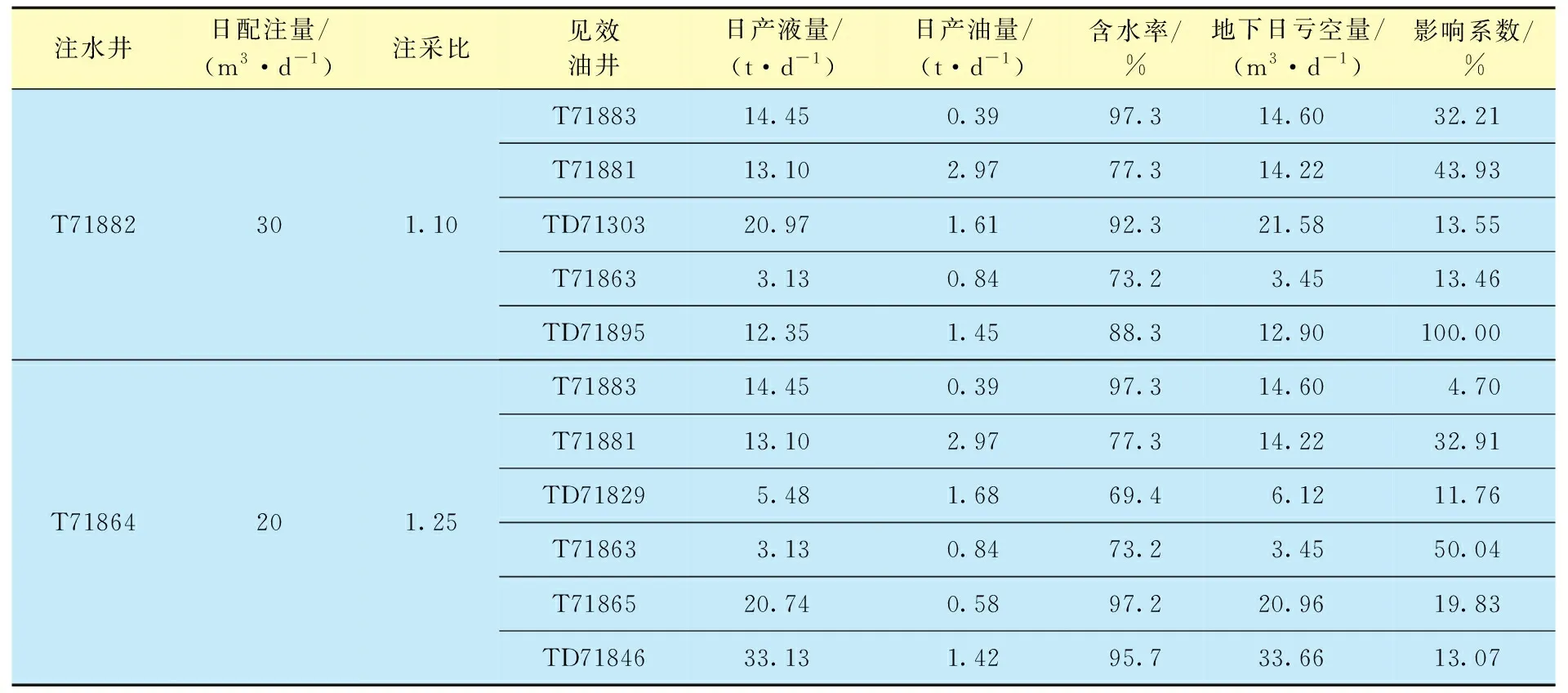
表3 井组配注计算结果Table 3 Calculation of wellgroup injection allocation
现场应用结果表明,改进注采连通分析模型能更科学地反映油田注采供需关系、更好地帮助技术人员制订井组配注方案。尤其是对于注采连通关系复杂、多向见效井较多的区块,能大大提高工作效率与方案的合理性。
4 结 论
(1) 考虑井底流压变化的多元线性回归注采连通关系分析模型能更准确地反映油井产量变化规律,可得到更准确、更符合生产开发实际的注采连通关系量化分析结果。
(2) 多元线性回归注采连通分析模型与井组配注模型相结合,有效解决了油田配注工作的效率问题,数据简单易得,可操作性强,对于实现油田智能调配具有重要的意义。
(3) 以改进型注采连通分析模型为基础的井组配注计算模型,在现场应用中得到了较好的验证,分析结果的准确性显著提升,可更好地辅助油田注采调配方案的制订。
