致密砂岩分形渗透率模型构建及关键分形参数计算方法
2020-09-14赵久玉王付勇
赵久玉,王付勇,杨 坤
(中国石油大学(北京),北京 102249)
0 引 言
准确预测致密砂岩渗透率并确定其关键影响因素对致密油藏高效开发具有重要意义。渗透率模型是预测储层渗透率的重要手段,实验室常利用经验公式拟合得到渗透率模型,Kozeny-Carman方程在预测常规砂岩的渗透率时具有良好的表现,在此基础上许多学者对其进行了改进[1-3],但致密储层孔隙结构复杂,孔隙类型多样,仅仅依靠孔隙度不能精确地预测储层渗透率。渗透率不仅与孔隙度有关,还与孔隙大小、分布、连通方式等有明显的关系[4]。分形理论可以有效表征复杂多孔介质孔隙分布特征,并在油藏储层评价中得到广泛的应用。国内外相关学者将分形理论与毛管束模型结合构建了不同的渗透率模型[5-11],但如何计算渗透率模型中的关键分形参数仍存在很大不确定性。
基于具有分形特征的迂曲毛管束模型,推导了特征单元中孔隙总流量表达式,得到致密砂岩绝对渗透率预测模型。利用压汞法提出了一种求取三维迂曲度分形维数的新方法,并利用渗透率模型对其合理性进行验证。研究表明,三维迂曲度分形维数计算与渗透率模型相结合,能够快速、准确地预测岩心渗透率,对致密砂岩储层物性评价具有重要意义。
1 渗透率模型
1.1 渗透率模型Ⅰ
Yu和Cheng[12]假设在一个长度为L0,2D的二维特征单元内,毛细管管径、长度均符合分形分布,建立一个无经验系数的渗透率模型:
(1)
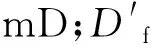
1.2 渗透率模型Ⅱ
Wang等[13]推导了迂曲度相等、孔隙大小符合分形分布的渗透率模型:
(2)
式中:φ为孔隙度;τ为平均迂曲度。
1.3 渗透率模型Ⅲ
在长度为L0,3D的立方体特征单元内,迂曲毛细管分布符合分形分布,根据分形理论,孔隙大小与累计孔隙数目满足[14]:
(3)

对式(3)求导可得:
(4)
特征单元内每根迂曲毛细管的长度也符合分形分布[12]:
(5)

Wang等[15]建立了单根毛细管长度具有分形特征的毛细管流量方程:
(6)
式中:L为迂曲毛细管长度,μm;q为单根毛细管流量,mm3/s;μ为流体黏度,mPa·s;p1、p2分别为毛细管两端压力,MPa。
根据分形理论,特征长度为L0,3D的特征单位中流体的流量Q可通过对单根毛细管流量从λmin到λmax积分得到,结合式(4)、(6)可得到特征长度为L0,3D的特征单元体中流体的流量Q为:
(7)
式中:Q为特征长度为L0,3D的特征单元体中流体的流量,m3/s。
将特征单元中的流量Q代入达西定律,则绝对渗透率的表达式为:
(8)
Yu[16]推导了三维迂曲度分形维数的表达式:
(9)
式中:τav为平均三维迂曲度;λav为平均孔隙直径,μm。
三维空间内,特征体单元边长L0,3D为[17]:

(10)
将式(9)代入式(10)变形可得:
(11)
(12)

2 渗透率模型参数计算
以26块鄂尔多斯盆地延长组的致密砂岩岩心为例,在渗透率模型Ⅲ的基础上,计算平均迂曲度、分形维数、特征长度和三维迂曲度分形维数,结果如表1所示。

表1 26块致密砂岩参数及模型参数计算结果Table 1 Model prediction and test data of 26 tight sandstone core samples

2.1 平均迂曲度
平均迂曲度是描述渗流通道的重要参数,Comiti和Renaud[18]、Yu[16]提出利用孔隙度计算平均迂曲度的方法,2种方法的计算结果存在一定的差异。由表1可知,τ1的数值为1~2;τ2的数值为3~6。虽然2种方法计算的平均迂曲度存在一定差异,但随着平均迂曲度增大,岩心渗透率降低,较大、较小的迂曲度都将影响岩心渗透率的计算准确性,选择合适的迂曲度计算方法会大大提高预测渗透率的准确性。
2.2 分形维数
分形维数用以表征孔隙的分布,Wang等[15]和Li[19]介绍了利用压汞曲线求取分形维数的方法。以1号岩心为例,使用2种方法得到的累计孔隙数目与孔隙直径的双对数曲线如图1所示,其斜率的负值为分形维数。Wang等计算出的分形维数接近2,并且孔隙半径和累计孔隙数目相关性较低(图1a)。Li计算的分形维数大于2,孔隙半径和累计孔隙数目相关性较好(图1b)。

图1 1号岩心N-λ双对数曲线

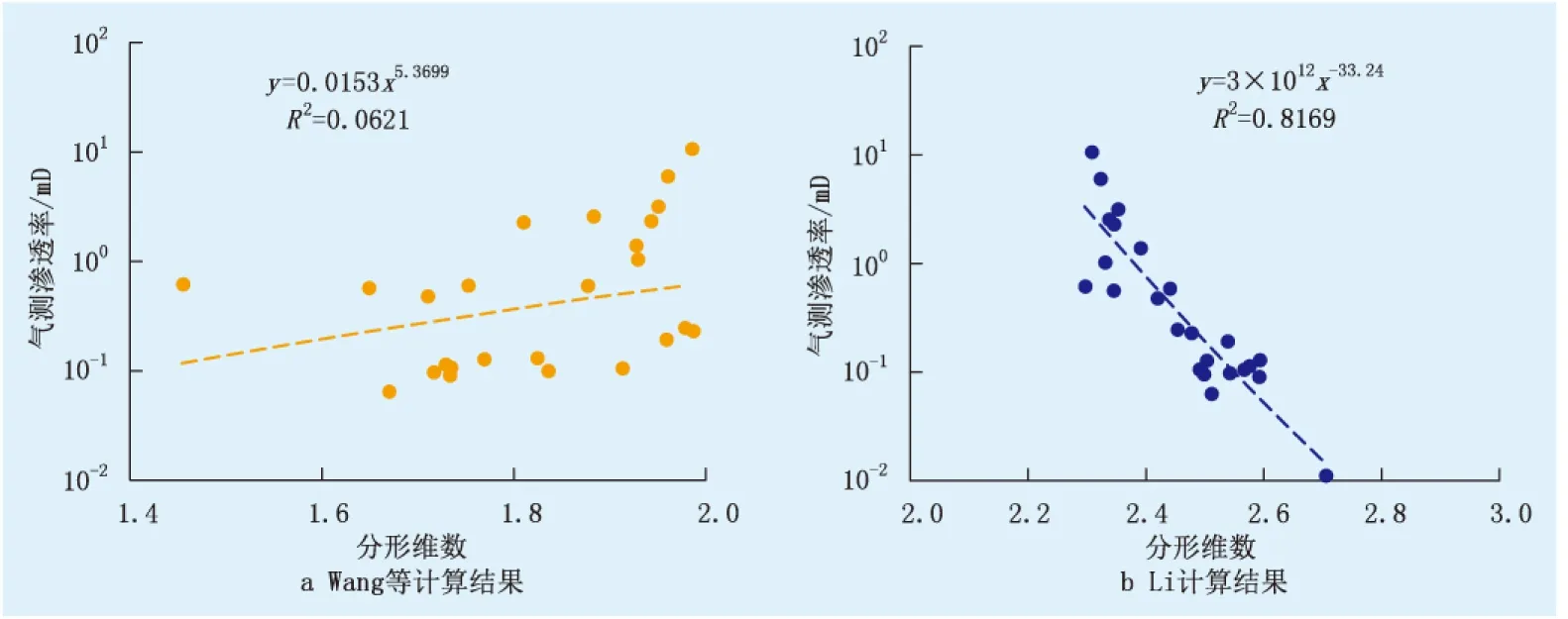
图2 分形维数与渗透率关系
2.3 特征长度和迂曲度分形维数
式(12)较为复杂,无法求得其解析解,信赖域算法是一种求解非线性优化问题的数值方法,该方法从给定的初始解出发,通过逐步迭代,不断改进,直到获得满意的近似最优解为止。将求得的三维特征长度代入式(9)可以计算得到三维迂曲度分形维数。
3 渗透率模型验证
岩心最大孔隙半径和平均孔隙半径可以通过压汞数据得到,由于压汞的进汞饱和度无法到达100%,因此,无法测量出准确的最小孔隙半径,此处假设最小孔隙半径均为1 nm。由上述3种模型可知,岩心内部孔隙迂曲度对岩心渗透率的计算有一定影响,而不同方法计算的迂曲度并不完全相同,存在一定的差异,因此,将2种方法计算的平均迂曲度分别带入上述3种渗透率模型,并对表1中26块致密砂岩渗透率进行模拟计算,将其与岩心气测渗透率进行对比,2种方法的计算结果分别如图3、4所示。图中拟合曲线与坐标轴角平分线的偏离程度可直观表述预测结果的准确性,拟合曲线与角平分线吻合度越高,偏离程度越小,渗透率预测越准确。

图3 平均迂曲度τ1预测渗透率与气测渗透率对比

图4 平均迂曲度τ2预测渗透率与气测渗透率对比
由图3可知,不同渗透率模型的计算结果不同。3种模型均考虑了岩心内部孔隙迂曲度对渗透率预测的影响,但其表现形式存在一定差异。模型Ⅰ中考虑了毛细管的迂曲分形特征,而模型Ⅱ中将所有孔隙迂曲度设为同一固定值,2种模型预测渗透率时所用的为二维迂曲度分形维数;模型Ⅲ中利用三维迂曲度方法进行计算。
同理,由图4可知,当利用Yu方法计算平均迂曲度时,利用渗透率模型Ⅲ所预测的渗透率与岩心气测渗透率最为接近。因此,利用三维迂曲度分形维数校正后的渗透率模型可以有效预测渗透率。
对比图3、4,由于2种方法所计算的迂曲度不同,二者渗透率预测结果也存在一定差异。表1中利用Comiti和Renaud方法计算的迂曲度略小于Yu方法所计算的迂曲度,因此,渗透率模型Ⅰ、Ⅱ计算所得的渗透率偏大,图3中的拟合曲线偏差略大于图4。
4 结 论
(1) 构建了一种基于孔隙大小分布和迂曲度分形特征的致密砂岩渗透率预测新模型,该模型没有经验系数,利用压汞曲线得到分形维数、最大孔隙半径与平均孔隙半径,并通过迭代法计算迂曲度分形维数、特征长度,即可对渗透率进行准确预测。
(2) 针对二维特征长度不能够准确表示迂曲度分形维数的问题,提出了一种求取三维迂曲度分形维数的新方法。以鄂尔多斯盆地延长组26个致密砂岩岩心为例,将计算所得三维迂曲度分形维数与渗透率模型Ⅲ相结合,所测得的渗透率与岩心气测渗透率最为接近,该方法可以有效地预测岩心渗透率。
(3) 不同方法计算的迂曲度不同,其预测渗透率结果也存在一定差异。当计算迂曲度较小时,渗透率预测结果偏大。选取合适的迂曲度计算方法对准确预测致密砂岩渗透率具有重要意义。
