基于多传感器数据融合的道岔区脱轨系数预测算法

2020-09-13杨桐董昱

铁道科学与工程学报 2020年8期

杨桐，董昱

杨桐，董昱

(兰州交通大学自动化与电气工程学院，甘肃兰州 730070)

针对目前车辆脱轨多发生在道岔区段，且现有脱轨评判方式考虑因素单一,不能全面评判轮轨接触安全性的问题，提出一种基于多传感器数据融合的道岔区脱轨系数预测算法。通过T-snake模型对车载摄像机获取的9号道岔区轮轨接触图像进行图像分割得到轮轨相对横向位移量；选用遗传算法优化的小波神经网络构建融合模型，输入相对位移量，速度量，加速度量以及轮重减载率进行数据融合预测脱轨系数。现场测试结果显示，利用该方法的预测脱轨系数模型考虑因素较为全面，且具有良好的精确性和鲁棒性。

脱轨；铁路道岔；数据融合；脱轨系数预测

道岔是铁路线路上的列车改变运行方向的关键部分，道岔区段轮轨关系较线路区段更加复杂，车辆脱轨事故频繁发生于道岔区段。因此，道岔区段的行车安全性更值得关注。铁路应用IEC 62290-1：2014标准文件中自动化程度最高等级GOA4定义为设备监控。基于此，通过多传感器数据融合方式研究道岔区段的行车安全，具有重要的现实意义[1−4]。目前，机器视觉活跃应用于各个领域。但近年来国内外学者多由轮轨接触模型通过动力学仿真来研究道岔区段的脱轨机理，在机器视觉多传感器数据融合方面考虑因素单一，检测精度低。马晓川等[5]根据基本轨与尖轨的相对位置及轨下支撑方式，分析轮轨接触特性，提出铁路道岔区轮轨两点接触计算方法。XU等[6]在考虑尖轨和基本轨的相对运动基础上，构建道岔有限元模型，通过动力学仿真软件研究轮轨接触关系。张鹏飞等[7]基于岔区轮轨系统动力学及轮轨接触关系理论，研究了固定辙叉结构不平顺对列车过岔动力特性的影响。王永胜等[8]提出了一种基于改进分水岭算法的彩色踏面图像分割方法，基于彩色梯度图像进行标记，由分水岭变换得到一次分割结果，通过图像连通域分割算法完成踏面的提取。陈皓等[9]提出了一种NARX神经网络算法预测脱轨系数的模型，但仅以轨道不平顺因素作为输入，存在考虑角度单一的问题。刘俊君等[10]提出了改进BP神经网络算法仿真预测脱轨系数的模型。输入为横移量，抬升量，速度值及接触角，未考虑加速度值且输入数据为仿真值，预测出的系数实际应用价值低。本文通过研究道岔区轮轨接触几何关系，以轨顶面中心线和踏面中心线的相对位移差为评判标准，确定了轮轨接触安全等级分类标准。通过图像分割对车载摄像机获取的轮轨接触区域图像帧进行特征提取，融合多传感器数据量作为小波神经网络的输入值预测出脱轨系数。多传感器数据融合算法架构如图1所示。如图1，轮对和钢轨的接触属于空间接触，且接触面不规则。由于轮轨过垂线的截面与钢轨过垂线的截面在同一平面内，因此可将三维接触转换为二维接触进行处理。首先，研究道岔区域轮轨间的几何接触关系，根据位移量确定出安全等级分类标准；然后，对车载摄像机获取的图像帧进行位移量特征提取。接着，建立多传感器数据融合模型，输入为位移量、速度、加速度和轮重减载率。根据遗传算法对融合模型网络参数进行优化。最后，由优化后的神经网络模型输出预测的脱轨系数来评价列车过叉安全性。

图1 多传感器数据融合算法架构

1 道岔区域轮轨接触几何关系

在铁路道岔转辙器部件内，车轮荷载由尖轨和基本轨共同承担。由于尖轨横截面几何形态的可变性导致轮轨接触关系复杂。根据基本轨与尖轨的相对位置及轨下支撑方式，以中国9号单开道岔为例，分析对比CHN60钢轨和磨损型LMA踏面匹配时的接触几何关系。LMA型踏面轮缘如图2(a)所示，不同断面处尖轨(轨顶宽分别为25，35和55 mm)与基本轨的空间位置关系如图2(b)，2(c)和2(d)所示。道岔区轮轨接触几何关系图如图3所示(以轨顶面35 mm为例)。

如图3，当车轮踏面与主次接触点的最小距离d，d为0时，踏面和轨顶面为一点接触或两点接触情况，该接触状态较为普遍；当轮对的横向位移较大时，车轮轮缘外侧和钢轨外侧面接触，出现爬轨情况。当轮对纵向位移角较大时，车轮与钢轨无接触点，出现跳轨情况[11−12]。综上，轮轨间的相对空间关系可用位移量进行划分。铁道科学院通过测量车轮抬升量实验将爬轨过程分为4个阶段，但实际运行中存在轨面不平顺等因素并且横向位移和纵向位移呈一一对应关系。在轮对轨道过轴线的垂向截面上，本文建立以二者中心线的位移差作为评判标准，该安全评判标准如表1所示。

(a) LMA型踏面；(b) 尖轨顶宽25 mm；(c) 尖轨顶宽35 mm；(d) 尖轨顶宽55 mm

图3 道岔区轮轨接触几何关系图

表1 位移安全评判标准

图4 车轮抬升量随时间变化曲线

2 图像特征提取

图像特征提取的目的是通过对车载摄像机获取道岔区轮轨接触图像帧，并对图像进行处理，进而得到轮轨间相对横向位移[13−14]。车载摄像机获取的图像可以实时监测轮轨间的接触状态，利用提取出的位移量使得后续多传感器数据融合预测脱轨系数更为准确。

2.1 图像预处理

为了得到较好的分割效果首先对图像进行预处理。以尖轨顶35 mm图像帧为例，获取原图如图5(a)所示，预处理步骤包括减少后续运算量的图像灰度化，结果如图5(b)所示；减少图像噪声的高斯滤波，结果如图5(c)所示；以及使得图像像素点灰度均匀化分布的直方图均衡化，结果如图5(d)所示。

(a)轮轨接触原图像；(b)预处理后原图像；(c) 高斯滤波后图像；(d) 直方图均衡化后图像

2.2 Snake模型基础

道岔轮轨接触区域灰度差异较小，车轮与钢轨存在相对运动性。选取对噪声和对比度不敏感snake模型对道岔区轮轨接触部分进行分割提取。

snake模型[13]为一种主动轮廓线模型，其思想为：由控制点构成的固定形状曲线，在定义力的作用下使曲线时刻保持连续平滑，并不断地朝着真实的轮廓线逼近。由能量函数定义snake模型中的目标轮廓线，其能量函数total定义为：

式中：第1项为内部能量int，第2项为外部能量ext，主动轮廓线在内、外力的共同作用下寻求其能量函数的极小值。其中内部能量int表达式为：

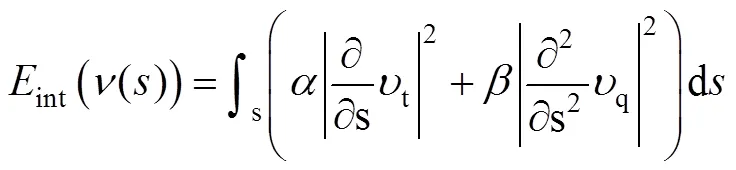
式中：第1项表示弹性能量，数值上等于v的1阶导数模平方与系数的乘积，其值决定着主动轮廓线的拉伸难易程度。第2项表示弯曲能量为v的2阶导数模，其数值决定着主动轮廓线的变形难易程度。外部能量表达式为：

令关于的微分项为：

当(,)的值达到稳定值时，即可求解出式(5)的值。

2.3 T-snake模型基础

T-snake(topology adaptive snake，拓扑自适应蛇模型) 模型是一种拓扑自适应主动轮廓模型。它是对传统的snake模型进行离散化处理后得到的，一定程度上解决了传统snake模型对初始目标轮廓选取敏感和弯曲函数对轮廓影响较小的问题。T-snake模型的思想是将连续曲线看做由个离散点构成，对于第个离散点其节点模型如图6所示，在T-snake模型中其内部能量函数int定义为：

式中：k1为弹性系数；k2为弯曲系数。xi+1，xi，xi−1为3个相邻的离散点，di为任意2个离散点之间的距离。

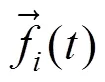
由上述公式可得，内外能量函数的和即为T-snake模型总能量，求解该能量极小值的过程思想和传统snake模型相同，也就是求解第个离散点微分近似项的稳定值。

2.4 改进T-snake模型提取道岔轮轨接触区

T-snake模型在继承了传统snake模型优点的同时，还是存在曲率约束不足，当图像背景和提取目标灰度差异较小时，分割效果不明显的问题。针对这些问题，本文在式(7)的基础上引入区域能量项Region，该区域能量项是基于局部区域的最小方差之上的，将外部能量函数重新定义为：

式中：为Region的比例值本文取2。Region的定义如下：

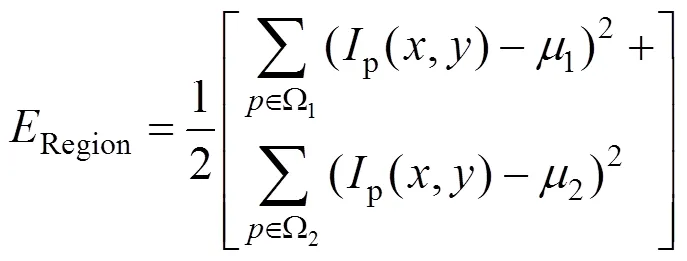
式中：(,)为的灰度值，W1为图像内部区域，1为灰度均值；相同的W2和2为外部区域和其灰度均值。式(8)中外力和膨胀力的计算公式如下：

式中：和分别为外力和膨胀力的系数。外力为高斯核函数与输入图像像素值卷积模平方与系数乘积的负数；膨胀力为第个离散点出单位法向量，二值函数和膨胀力幅度值三者乘积的倒数。当像素值大于阈值时二值函数((,))取正，反之取负。通常情况下为常数，为了提高收敛速度和算法的稳定性，本文将定义为：

式中：W为离散点的3×3的邻域，为该领域内最大最小灰度值之差，和为灰度方差以及灰度均值。

2.5 分割结果分析

基于上，为了验证提出算法的分割效果，在MATLAB仿真软件中，选用兰州铁路局兰州北编组站提供的道岔区轮轨接触图像作为输入图像，采集的图像中线路钢轨材质为U71Mn，其型号为CHN60轨，道岔号为9号道岔，车轮踏面型号为LMA-30，具体实验环境设备参数如表2所示。

表2 实验环境设备参数

实验中相关参数取值如下：参考snake算法在图像分割方面的应用[13]，式(3)中控制图像外部能量的系数为5.0，平滑函数中的高斯核函，数()为1.35。分别对尖轨顶25进行道岔区踏面边缘分割，结果如图7所示。

(a) 原图像；(b) 预处理图像；(c) 初始轮廓线；(d) Snake 分割；(e) T-snake分割；(f) 本文分割结果

由图7(d)，7(e)和7(f)可得，轮缘凹陷处局部(矩形内部分)的分割效果为本文改进后T-snake算法效果最优，对凹陷处边缘捕捉能力比snake和未优化的T-snake算法要强，T-snake模型对凹陷处边缘捕捉能力优于snake模型。为了客观地评价本文算法的分割结果，引入算法迭代次数，普拉特品质因数(Pratt’s figure of merit，PFM)和标准误差(Standard Error，SE)这2个评价标准。PFM和SE的计算方法如下：

式中：s为实际实验中提取像素点的个数；l为理想标准情况下提取出像素点的个数；为第个提取点到真实点的距离；为距离系数，本文取5。s为实际提取的边缘特征值；为理想情况标准边缘特征值。通过式(12)和式(13)可以得出，当PFM的值越大且SE的值越小时，提取的踏面边缘越接近于真实边缘。

在道岔区轮轨接触输入图像中，手动提取车轮轮缘踏面的边界，将其作为理想标准情况下的目标边界，分别采用标准snake，标准T-snake和本文改进后的T-snake算法的实验结果进行对比，并结合算法的迭代次数多角度进行评价，具体实验结果评价标准如表3所示。

表3 实验结果评价标准

从客观评价标准上来看，本文提出的算法在提取轮轨接触图像中踏面的边缘的实验中PFM与SE系数，以及算法迭代次数与收敛时间上优于其他3种分割方法。

3 多传感器数据融合

3.1 融合模型构建

本文采用非线性逼近和容错能力强的小波神经网络构建多传感器输入融合预测模型。该模型的输入数据为道岔区轮轨相对横向位移量，列车速度值，列车加速度值，轮重减载率。由参考文献[14]隐含层节点数为5，输出为预测值脱轨系数。得到融合模型如图8所示[14]。

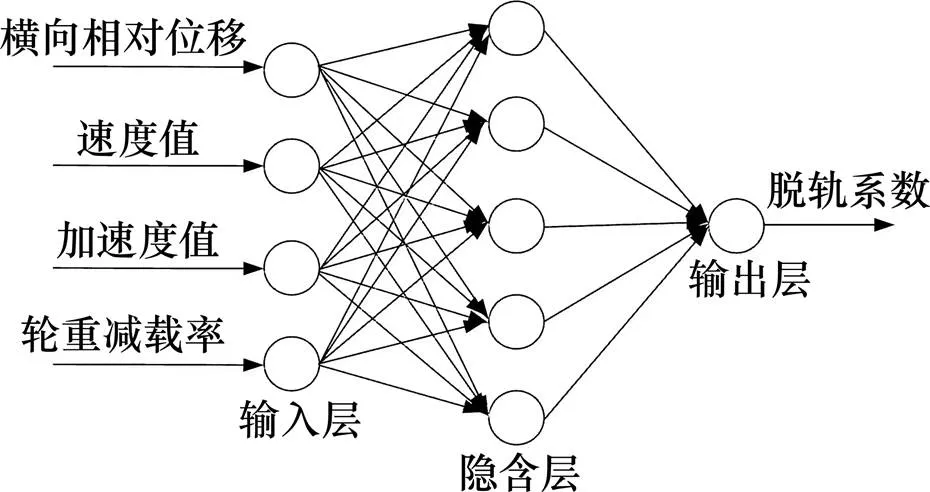
图8 脱轨系数预测融合模型

1) 输入层：()=[x()x()x()x()]T，1()为道岔区轮轨相对横向位移量，2()为列车速度值，3()为列车加速度值，4()为轮重减载率。

其中，速度值由速度传感器获取；加速度值由加速度传感器获取；轮重减载率由测力传感器获取；道岔区轮轨相对横移量是通过对车载摄像机获取的轮轨接触图像进行分割，由分割得到的边缘曲线确定轮轨中心线计算得到的，的计算方法如下：

式中：0为单个像素的长度；为提取出的踏面边缘中心线和钢轨中心线间的像素点个数，具体计算示意图如图9所示。

2) 隐藏层：计算公式如下。

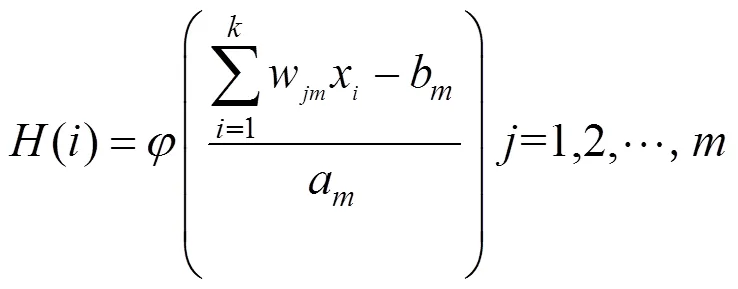
式中：()为隐含层第各节点输出值；w为输入层和隐含层的连接权值；b为平移因子；a为尺度变换因子；为小波基函数，选用Morlet母小波函数，计算公式如下：

3) 输出层：计算公式如式(14)所示。

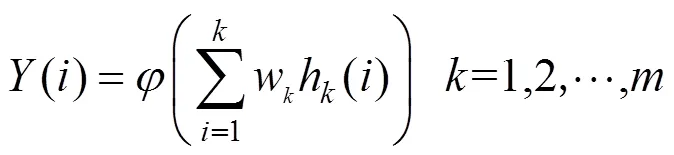
式中：hk(i)为隐含层第i各节点输出值；wk为输出层和隐含层的连接权值；k为隐含层节点数；m为输出层节点数。

3.2 GA优化融合模型参数

脱轨系数融合模型是由小波神经网络构建的。本文拟采用GA遗传算法来优化融合模型的参数，使网络收敛速度加快，融合结果精度提高。遗传算法优化小波神经网络包括网络结构的确定、遗传算法优化网络初始参数。其具体步骤如下。

1) 参数编码：每个染色体编码为(wwba)形式的实数串。

2) 适应度函数：训练小波神经网络后，预测输出和期望输出之间的误差绝对值和即个体适应度值。

3) 选择操作：每个个体被选择的概率为：

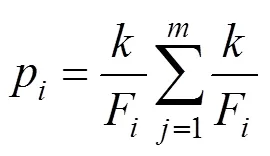
式中：F为个体的适应度值；为概率系数，为种群个数。

4) 交叉操作：采用实数交叉法。

5) 变异操作：基因a进行突变操作。

3.3 优化结果

基于以上阐述，在matlab2016a软件平台中进行融合模型参数优化实验，算法中，种群规模=20，进化代数为50，初始交叉概率0=0.7，最优个体适应度值如图10所示。

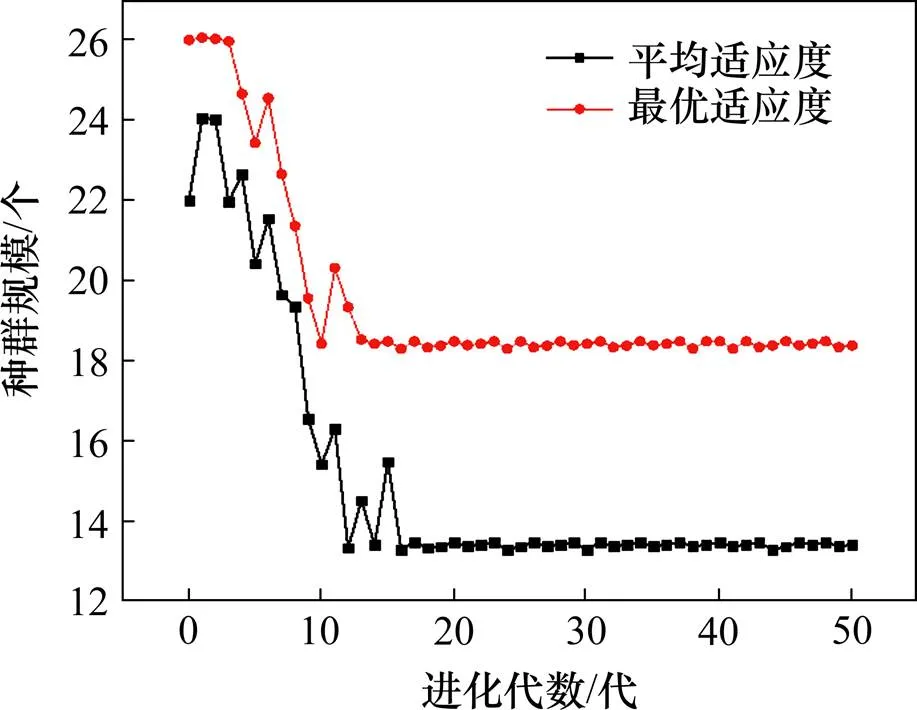
图10 最优个体适应度值

从图10可以看出，在仿真运行到15代左右，最优个体的适应度值已趋于稳定，表明遗传算法已得到优化的融合模型参数，具体数值见表3。

表3 优化后融合模型参数

4 仿真实验与结果分析

现场实验地点为兰州铁路局兰州北编组站线路。机车型号为东风7C型，钢轨型号为CHN60轨，道岔为9号道岔。道岔线路长700 m，以2 min为采样周期，共取200组数据，每20组数据为一个样本，分为训练集和测试集。现场多传感器数据及融合后的部分脱轨系数如表4所示。预测误差对比如图11所示。

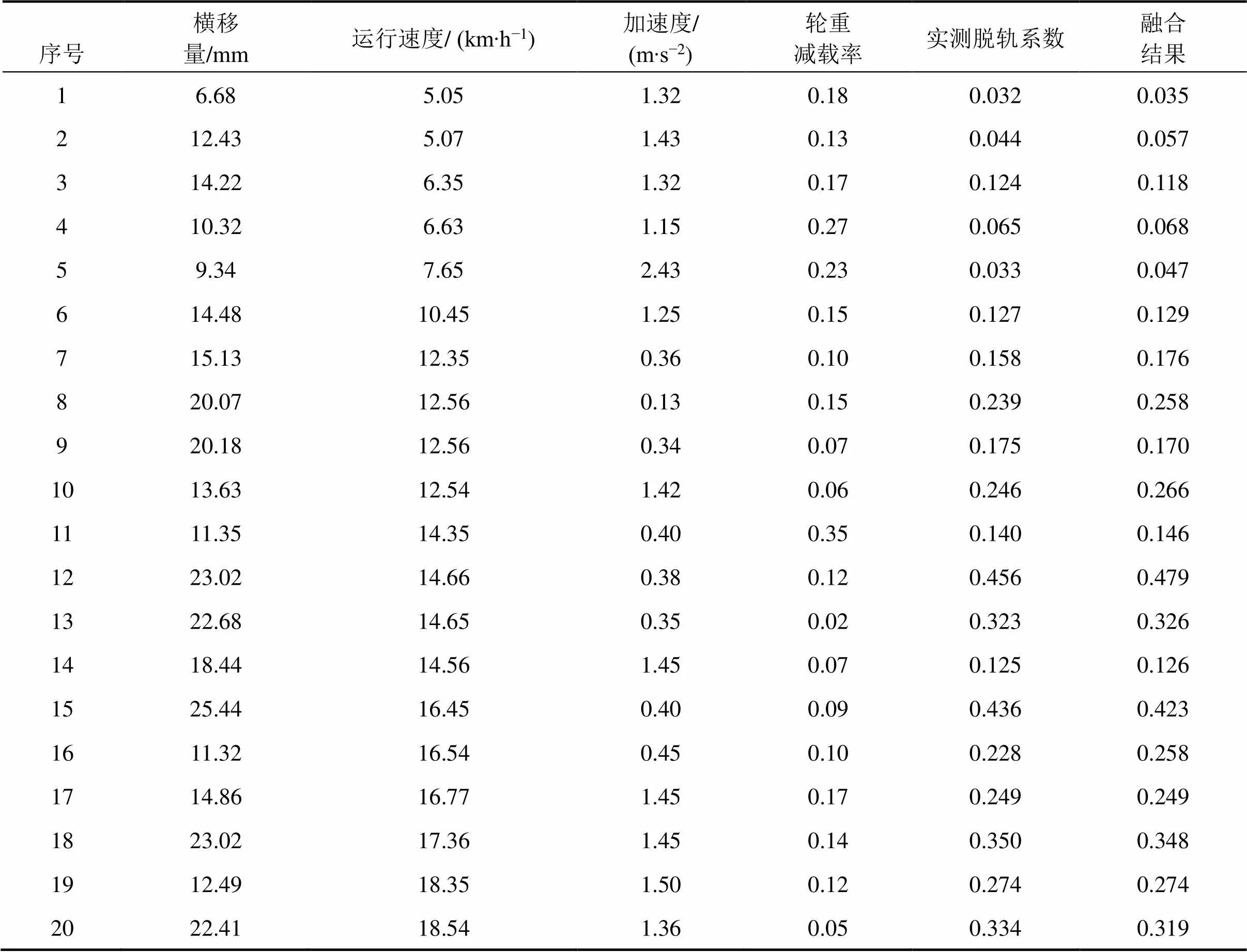
表4 初始数据及融合结果

从图11可以看出，融合结果的误差在4%范围内，预测结果良好。主要误差存在的原因为输入的相对位移量，因为图像分割结果与真实踏面边缘像素点存在一定的误差。总体来看，融合数据与实测数据吻合度良好，满足阈值要求，融合后的脱轨系数对于过岔安全性研究具有一定的意义。

图11 融合结果误差对比

通过观测表4中输入数据对融合结果影响可以客观地评价本文融合模型与实际脱轨理论的吻合度。以轮对相对横移量为基础坐标轴，绘制速度，加速度及轮重减载率与融合结果的三维示意图如图12，图13和图14所示。由图可得，本文实测数据与预测脱轨系数的关系符合脱轨理论。

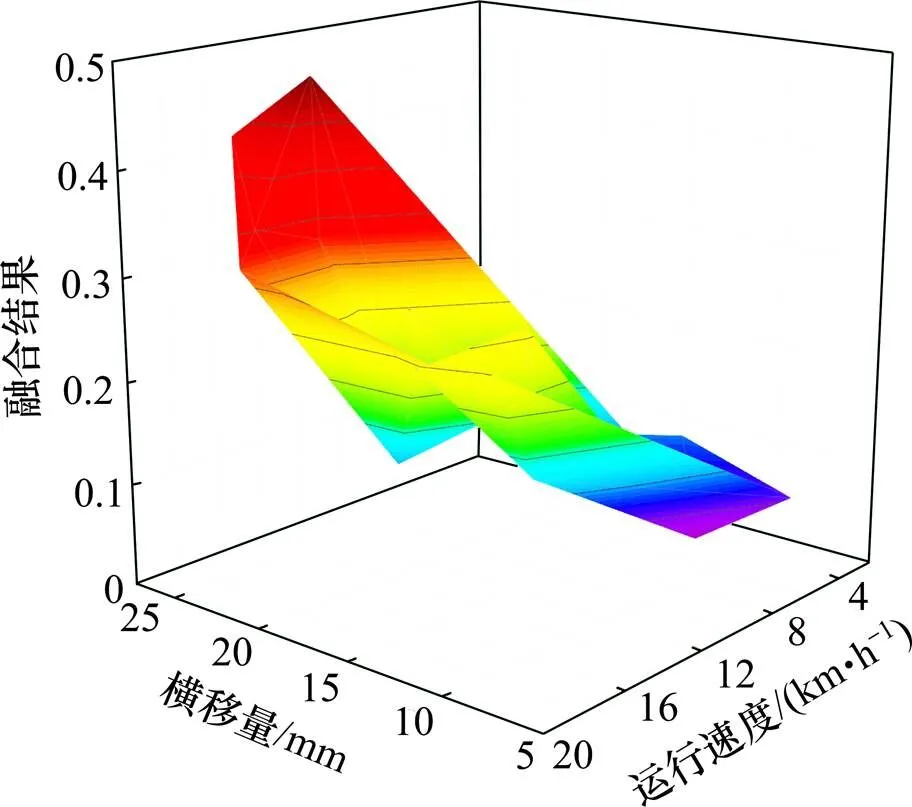
图12 运行速度对融合结果的影响

为了避免了样本数据过学习以及欠学习情况的发生，实验采用10折交叉验证方法，将200个样本数据随机分成10组，每20个数据为一个样本统一编号，进行10组预测实验。第次实验中，第10组样本数据为测试数据，其余9组(180个样本数据)为训练数据。同时对本文模型、单一小波神经网络、文献[9]中的NARX神经网络和文献[10]中的改进BP神经网络4种预测模型进行对比实验，分别取平均相对误差和最大相对误差，结果如图15和图16所示。

图13 加速度对融合结果的影响

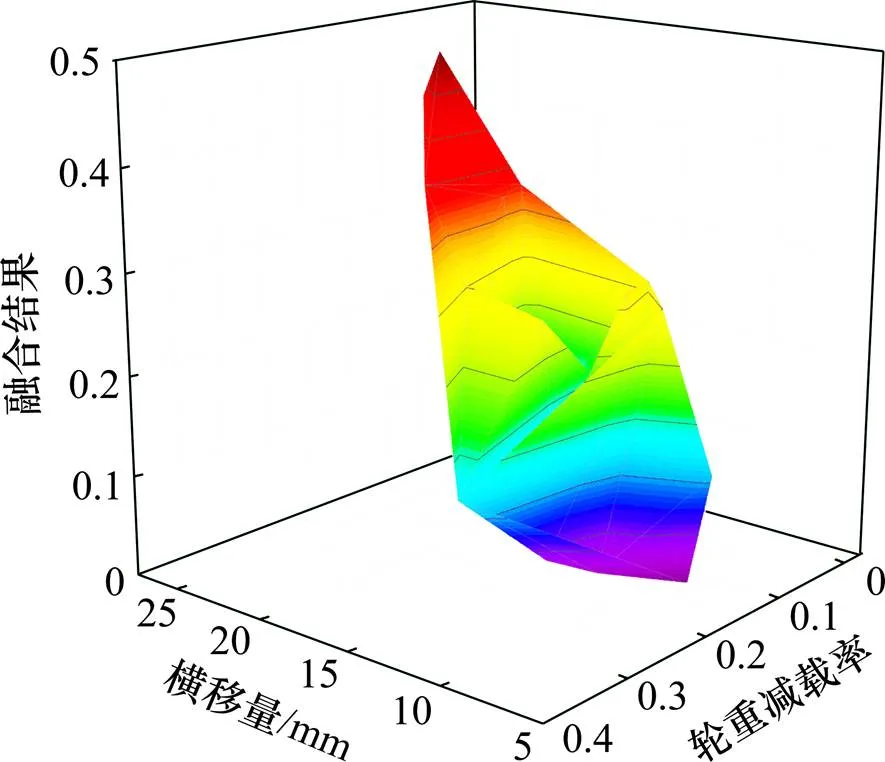
图14 轮重减载率对融合结果的影响

图15 平均相对误差结果图

图16 最大相对误差结果图

由图15~16可知，10次交叉实验的4种预测模型中，本文预测模型平均相对误差和最大相对误差较单一小波神经网络预测模型和文献[9]文献[10]预测模型要低，本文模型的平均相对误差基本在 1.6%~2.9%波动，最大相对误差基本在2.2%~3.8%波动。从图16可知，4种模型最大相对误差值均未超过6.5%，因此，对每种预测模型的10次测试按相对误差在1%~2%，2%~3%，3%~4%，4%~5%，5%范围外的样本组进行统计，并换算成比例。4种模型的相对误差分布情况对比如表5所示。

表5 预测模型相对误差分布

表5中，模型1为单一小波神经网络，模型2为改进BP神经网络，模型3为NARX神经网络，模型4为本文模型。由表5可以看出，本文模型预测的相对误差分布在1%~2%和2%~3%范围区间内的比例要比其他3种预测模型高，而大误差的概率远低于其他3种预测模型。这说明，该模型具有良好的稳定性和预测结果的精确性。

5 结论

1) 针对现有动力学仿真研究方法研究脱轨机理不具有现实监测列车过叉运行安全性问题，采用多传感器实时监测采集的数据作为输入进行脱轨系数的预测。

2) 特征量提取部分，引入区域能量项对T-snake算法进行改进。实验结果表明，本文算法提取效果良好且分割精度优于标准snake和T-snake算法。

3) 构建多传感器数据融合模型进行脱轨系数的预测，并对预测模型进行交叉验证。实验结果显示，本文提出的模型合理且具有良好的鲁棒性，有较高的理论价值和实际应用前景。

[1] 王健. 基于轮轨关系的小号码道岔转辙器区脱轨机理研究[D]. 成都: 西南交通大学, 2018. WANG Jian. Study on derailment theory of switch area in small number turnouts based on wheel-rail relationship [D]. Chengdu: Southwest Jiaotong University, 2018.

[2] WANG P, WANG J, MA X, et al. Theoretical 3D model for quasi-static critical derailment coefficient of railway vehicles and a simplified formula[J]. Mathematical Problems in Engineering, 2018(10)：1-13.

[3] 易思蓉. 铁道工程[M]. 2版. 北京: 中国铁道出版社，2009. YI Sirong. Railway engineering[M]. 2nd ed. Beijing: China Railway Press, 2009.

[4] 王平. 高速铁路道岔设计理论与实践[M]. 成都: 西南交通大学出版社, 2011. WANG Ping. Design theory and practice of high-speed railway turnout [M]. Chengdu: Southwest Jiaotong University Press, 2011.

[5] 马晓川, 徐井芒, 王平, 等. 铁路道岔转辙器部件轮轨两点接触计算方法研究[J]. 铁道学报, 2019, 41(7): 155−161. MA Xiaochuan, XU Jingmang, WANG Ping, et al. Research on calculation method of wheel-rail two-point contact of railway turnout switcher components[J]. Journal of the China Railway Society, 2019, 41(7): 155− 161.

[6] XU J M, WANG P L. Effects of profile wear on wheel-rail contract conditions and dynamic interaction of vchicle and turnout[J]. Advances in Mechanical Engineering, 2016, 8(1): 1−14.

[7] 张鹏飞, 朱旭东, 雷晓燕. 提速道岔辙叉翼轨的加高值方案优化[J/OL].西南交通大学学报: 1−9[2019−11−28]. http://kns.cnki.net/kcms/detail/51.1277.U.20190918.1049.011.html. ZHANG Pengfei, ZHU Xudong, LEI Xiaoyan. Optimization of the raising value scheme of turnout wings for speed increase turnout[J/OL]. Journal of Southwest Jiaotong University: 1−9[2019−11−28]. http:// kns.cnki.net/kcms/detail/51.1277.U.20190918.1049.011.html.

[8] 王永胜, 马增强, 宋子彬, 等. 基于图像畸变校正的车轮踏面区域提取[J]. 图学学报, 2018, 39(3): 432−439. WANG Yongsheng, MA Zenqiang, SONG Zibin, et al. Wheel tread area extraction based on image distortion correction[J]. Journal of Graphics, 2018, 39(3): 432−439.

[9] 陈皓, 程晓卿, 俞秀莲, 等. 列车脱轨系数的精确预测方法研究[J]. 计算机仿真, 2013, 30(7): 142−146. CHEN Hao, CHENG Xiaoqing, YU Xiulian, et al. Study on the prediction method of train derailment coefficient[J]. Computer Simulation, 2013, 30(7): 142− 146.

[10] 刘俊君, 校美玲, 陈明义. 基于轮轨接触关系的列车运行安全预测仿真研究[J]. 石家庄铁路职业技术学院学报, 2019, 18(3): 47−52. LIU Junjun, XIAO Meilin, CHENG Mingyi. Simulation study on train safety prediction based on wheel-rail contact relationship[J]. Journal of Shijiazhuang Railway Vocational Technology College, 2019, 18(3): 47−52.

[11] Elias Kassa, Jens C O. Nielsen. Dynamic train–turnout interaction in an extended frequency range using a detailed model of track dynamics[J]. Journal of Sound and Vibration, 2008(4): 893−914.

[12] 翟婉明, 陈果. 根据车轮抬升量评判车辆脱轨的方法与准则[J]. 铁道学报, 2001(2): 17−26. ZHAI Wanming, CHEN Guo. Methods and criteria for judging vehicle derailment based on wheel lift[J]. Journal of the China Railway Society, 2001(2): 17−26.

[13] 周春瑜, 程显毅. 自适应滤波结合改进T-Snake模型的甲状腺超声图自动分割方法[J/OL]. 计算机应用研究: 1−4[2019−11−28].https://doi.org/10.19734/j.issn.1001-3695.2018.09.0787. ZHOU Chunyu, CHENG Xianyi. Automatic segmentation of thyroid ultrasound map based on adaptive filtering and improved T-Snake model[J/OL]. Application Research of Computers: 1−4[2019−11−28]. https://doi.org/10.19734/j.issn.1001-3695.2018.09.0787.

[14] 路学海, 潘迪夫, 韩锟, 等. 基于改进的QPSO-WNN滚动算法的铁路沿线短期风速预测[J]. 铁道科学与工程学报, 2016, 13(5): 978−984. LU Xuehai, PAN Difu, HAN Kun, et al. Short-term wind speed prediction along railway line based on improved QPSO-WNN rolling algorithm[J]. Journal of Railway Science and Engineering, 2016, 13(5): 978− 984.

Prediction algorithm of derailment coefficient in turnout area based on multi-sensor data fusion

YANG Tong, DONG Yu

(College of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

For the current vehicle derailment occurred in the switch section, and the existing way of derailing judge to consider a single factor can not fully judge the security issue of wheel-rail contact, an algorithm for predicting derailment coefficients in turnout areas based on multi-sensor data fusion is proposed. The method used the T-snake model to segment the wheel-rail contact image of the No. 9 turnout area acquired by the vehicle camera to obtain the relative lateral displacement of the wheel-rail. The wavelet neural network optimized by genetic algorithm is used to construct the fusion model. The input data is the relative displacement amount, speed amount, acceleration amount, and wheel load reduction ratio to perform data fusion to predict the derailment coefficient. The field test results show the accuracy of the derailment coefficient predicted by this method is high, and the considerations are comprehensive.

derailment; railway turnout; data fusion; derailment coefficient prediction

U213.6