高中数学教学中数形结合思想的应用
2020-09-12李彩琴
李彩琴

【摘要】文章简单介绍了数形结合思想,分析了其在高中数学教学中的重要性,并从准确把握思想应用原则,循序渐进强化学生意识,深度引导学生感悟思想,针对不同问题合理应用等方面,对于高中数学教学中合理、有效应用数形结合思想的策略展开了探讨,以供同行参考。
【关键词】高中数学教学;数形结合思想;应用
要想有效提高数学教学效果,就必须对过于强调课堂讲解与机械式重复的传统教学模式进行创新、调整与优化,尤其要突出学生主体性,重点培养学生数学核心素养。其中,在教学中合理应用数形结合思想,不仅可以让教学过程变得更为简单,而且能有效促使学生主动思考,培养学生的逻辑思维能力以及多角度思考问题、灵活变通与解决问题的能力,是极具实践价值的教学创新方式。
一、数形结合思想及其在高中数学教学中的重要性
所谓数形结合思想,就是将数学中所研究的数与形进行联系与结合,从而达到借助数的精确性来阐明形的某些属性,或者借助形的几何直观性来阐明与数之间的某种关系。简单而言,数形结合思想就是以数解形或者以形助数,充分利用数与形之间的密切联系,实现二者的相互利用。对高中数学教学而言,渗透与融入数形结合思想十分有必要。
首先,数与形是高中数学研究的基础对象,基本上所有教学内容都绕不开二者,而且二者又有着密切联系,因而合理应用数形结合能够在很大程度上促使复杂问题简单化、抽象问题具体化,对帮助学生掌握知识、解决问题有着重要意义。
其次,在教育改革背景下,高中数学教学不能再停留和局限于知识传授,而是要引导学生全方位发展。在教学中合理渗透数形结合思想,能够对学生思考问题能力、创新思维、逻辑思维等进行有效培养,促使学生养成良好的学习习惯,拓展学生解题思维和思考问题的思路,有助于学生全面成长与发展。
二、高中数学教学中数形结合思想的应用策略
1.准确把握思想应用原则
在数学教学中应用数形结合思想时,不管是基于该思想进行知识讲解、难题解答,还是培养学生相应的数学思想解题方法,都需要遵循一定的基本原则。
首先,应当遵循双向性原则,即数与形是相互对立又联系紧密的两个层面,在对二者进行思考时一定要进行双向思考,不能只通过数对形来进行研究,也不能局限于数对形的表现。只有充分贯彻双向性原则,才能真正做到对数与形的有效统一与灵活应用,保障其在数学教学中发挥应有的作用。
其次是簡洁性原则。无论是讲解知识还是解答难题,教师在应用数形结合思想时,都是为了用更加简单直观的方式呈现内容,帮助学生以更容易理解和掌握的形式进行思考与探索,从而提高教学效率,提升学生解题速度与准确性。
再次是等价性原则。在数与形在相互转换的过程中,一定要保证对等等价,但凡其中存在一点偏差,都可能导致数形结合思想与方法的运用存在问题,影响最终的解题结果准确性。
最后是创新性原则。数形结合思想虽然在高中数学中占据着极其重要的地位,但这并不意味着学生在解决任何数学问题时都可以应用该思想。只有根据实际情况创新性地应用该思想,才能最大限度地发挥其作用,促使学生更快更准确地解决问题,否则容易陷入解题误区;过于依赖数形结合而无法掌握其他数学思想及方法,更可能导致思维固化。
2.循序渐进强化学生意识
在数学教学中应用数形结合思想具有多重目的,其中最基础的一点在于引导学生以更加简单易懂的方式学习知识,解决难题。从更深层次的应用目的考虑,则要以培养学生良好的数形结合思想与灵活的运用方法为关键,确保学生能够合理利用该思想自主学习与探索,同时促进学生全面发展。不过,思想的渗透与培养是一项长期工作,不可能通过短期教学有效实现,教师必须充分意识到这一点,并在教学实践中以兴趣培养为重要基础,循序渐进地强化学生意识,一步步地培养学生良好的数形结合思想,让学生科学运用数形结合方法进行思考与解题。因此在日常教学中,教师一定要对教学内容进行深度挖掘,着重分析其中与数形结合有着密切联系的部分,并针对这部分进行合理设计,以数形结合的方式带领学生学习新知识,从而让学生在不知不觉间理解、接受和习惯该思想。
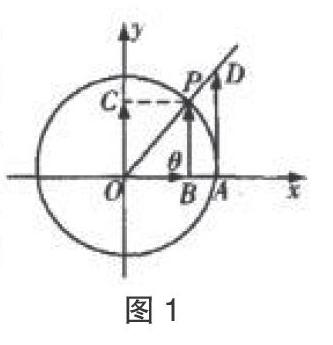
例如在教学三角函数相关内容时,教师可以利用单位圆帮助学生理解新知识。通过图1所示的单位圆,教师可以直观地向学生展示有向线段,并将该图形与三角函数的定义进行紧密联系、数形结合。教师以单位圆中的有向线段OB、OC、OP、OA、AD等,带领学生学习角θ的正弦线、余弦线、正切线等,从而帮助学生快速、准确地理解知识点。由于单位圆和有向线段都是学生容易理解且较感兴趣的内容,教师利用二者并应用数形结合思想,能够在直观讲解知识的同时激发学生兴趣,强化学生数形结合意识。
3.深度引导学生感悟思想
数学教学中对数形结合思想的应用不能停留在简单的认知上,更要引导学生对其进行深度感悟,从而促使学生掌握灵活运用该思想及方法的有效方式。对此,教师一定要通过各种方式引导学生进行感悟,促使学生灵活地主动进行数转形以及形转数,更加高效地运用数形结合方法解决问题。要想真正促使学生进行深度感悟,一定要从学生既有知识储备出发,让学生对已掌握知识进行深度挖掘和探索。
例如在教学函数相关内容时,教师要求学生画出一次函数与二次函数的图像,并让学生结合图像对函数本质、特征等进行研究,鼓励学生自主探索、合作学习。学生在教师的指导下,对函数图像进行反复研究,合作讨论,一起探讨图像表现了函数的哪些特征,并发现函数单调性、奇偶性、对称性等均在图像上得到有效体现。如此一来,学生对数形结合有了更为深刻的认知,并能真正将该思想作为学习数学和解决数学问题的重要工具。
4.针对不同问题合理应用
数形结合体现在高中数学的方方面面,故而合理应用该思想可以更加简单、直观、高效、准确地解决不少数学难题。尤其是对一些依靠常规方法难以有效解决的数学问题而言,灵活应用数形结合方法往往能起到奇效。综观高中数学内容,诸如集合、函数、方程与不等式、三角函数、数列、解析几何、立体几何、绝对值、概率及统计等相关问题的解决都可以应用数形结合思想。在进行这些内容的教学或者解决相关内容时,教师需要针对性地引导学生合理应用数形结合思想,培养学生相应的解题习惯,确保学生更加高效地解决不同的问题。
以函数问题与解析几何问题为例,二者的解答可以通过常规方式完成,也可以利用数形结合方法完成,只不过在实际应用时有一定区别,教师需要针对二者的数形结合解题方法进行准确教学。其中,函数问题应用数形结合思想的关键在于应用形来对数进行直观表现,如此既能快速解决问题,也能避免大量复杂运算而导致的运算出错问题;而解析几何问题中运用数形结合思想,关键就在于将几何结构代数化,利用数来对形进行表达和反映,从而更加具体、准确地进行解答。
例如函数问题:已知f(x)=x2-2ax+2,当x≥-1时,f(x)>a恒成立,试求取a的取值范围。
解析几何问题:已知二元一次方程3x+4y=12,且x≥0,y≥0,求M(x,y)=x2+y2-12x-2y+37取得最大值与最小值的点的坐标。
在应用数形结合思想解决这两个问题时,教师要画出相应的图形,分别如图2和图3所示,让学生根据图形解答问题。
在解决函数问题时,应当将重心放在图形对代数语言的表达上,引导学生结合题意对图形进行观察,并代入问题中给出的条件进行思考,从而求出a的取值范圍。学生在教师的引导下,观察图形,代入题目给出的条件,思考当△<0和△≥0时的不同情况,确定两种情况下a的取值范围分别为(-2,1)和(-3,1),从而判断出答案为(-2,1)。
而在解决解析几何问题时,教师带领学生对画出的图形进行研究,直接通过观察图像可得知x的取值范围为[O,4],并将M(x,y)变形为M(x,y)=(x-6)2+(y-1)2,那么M(x,y)就代表动点P到定点Q的距离的平方,可直接通过观察图形得知点A和点B是M(x,y)取得最大值与最小值的点的坐标。
三、结语
高中数学教学中应用数形结合思想极其有必要,不仅可以更加简单高效地传授知识和解决问题,而且能有效培养学生良好的解题思维与习惯。教师在教学实践中应当积极探索合理渗透、融合与应用数形结合思想的有效路径,尽量以更加简单、直观而高效的方式带领学生学习,提高教学水平,促进学生数学水平全方位提升。
【参考文献】
[1]韩伟会.浅谈高中数学教学中数形结合思想的应用[J].课程教育研究(学法教法研究),2017(07):68.
[2]李晓明高中数学教学与解题中数形结合思想方法的应用分析[J].中国新通信,2018(07):209.
[3]张晓光.分析如何在高中数学教学中渗透数形结合思想[J].中国校外教育(上旬),2016(08):103.
[4]杨德源.高中数学教学中数形结合思想的应用现状及策略研究[J].中国农村教育,2019(33):68.
[5]王宝志.探究高中数学教学中数形结合思想的有效应用[J].数理化解题研究,2017(10):35-36.
