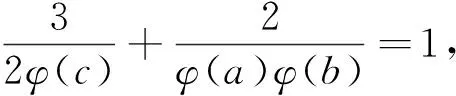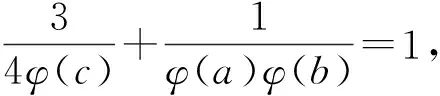三元变系数混合型欧拉函数方程φ(abc)=3φ(a)φ(b)+4φ(c)的可解性
2020-09-12梁晓艳
高 倩,高 丽,梁晓艳
(延安大学 数学与计算机科学学院,陕西 延安 716000)
0 引言
对于任意正整数n,欧拉函数φ(n)表示1,2,…,n-1中与n互素的正整数的个数。欧拉函数φ(n)是数论中极为重要的一类函数,而有关该方程解的研究也是数论中极具意义的研究课题之一。引起了不少数论学者的关注,也得到了一些结论。如文献[1]得出方程φ(mn)=k(φ(m)+φ(n))在k=3时的部分解,而文献[2-4]得出该方程在k=3,4,5,6时的全部解,而文献[5-7]得出方程φ(xyz)=k[φ(x)+φ(y)+φ(z)]在k=3,4,5时的全部解,张四保[8]研究了欧拉函数方程φ(ab)=kφ(a)φ(b)的可解性问题,本文在上述文献的启发下研究φ(abc)=3φ(a)φ(b)+4φ(c)的可解性问题,并给出了该方程的全部正整数解。
1 相关引理

其中p1,p2,…pk为素数。
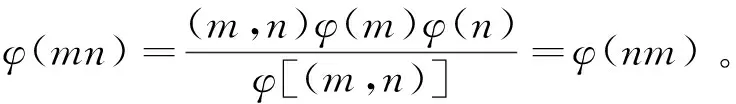
引理3[9]当n≥2时,φ(n) 定理三元变系数混合型欧拉函数方程φ(abc)=3φ(a)φ(b)+4φ(c)有共计87组正整数解,即为下述 φ(a,b,c)=(1,17,5),(1,17,8),(1,17,10),(1,17,12),(1,32,5),(1,34,5),(1,48,5),(2,17,5),(3,16,5),(16,3,5),(17,1,5),(17,1,8),(17,1,10),(17,1,12),(17,2,5),(32,1,5),(34,1,5),(48,1,5)(1,15,7),(1,16,7),(1,20,7),(1,24,7),(1,30,7),(1,16,9),(1,20,9),(1,15,14),(2,15,7),(3,5,7),(3,8,7),(3,10,7),(3,5,14),(4,5,7),(4,5,9),(6,5,7),(5,3,7),(5,3,14),(5,4,7),(5,4,9),(5,6,7),(8,3,7),(10,3,7),(15,1,7),(15,1,14),(15,2,7),(16,1,7),(16,1,9),(20,1,7),(20,1,9),(24,1,7),(30,1,7),(2,15,4),(2,16,3),(2,20,3),(1,16,4),(1,20,4),(1,24,4),(4,5,6),(4,10,3),(3,8,4),(4,5,4),(4,8,3),(3,10,4),(10,3,4),(10,4,3),(5,4,6),(5,6,4),(5,4,4),(8,3,4),(8,4,3),(30,1,4),(16,1,6),(20,1,6),(16,2,3),(20,2,3),(15,2,4),(2,8,2),(2,10,2)(2,12,2),(4,4,2),(4,6,2),(6,4,2),(10,2,2),(12,2,2),(8,2,2),(16,1,4),(20,1,4),(24,1,4)。 证明对于三元变系数混合型欧拉函数方程 φ(abc)=3φ(a)φ(b)+4φ(c) (1) =3φ(a)φ(b)+4φ(c)≤7φ(a)φ(b)φ(c) (1)当φ(c)=4,φ(a)φ(b)=16时,得φ(c)=4,φ(a)=1,φ(b)=16;φ(c)=4,φ(a)=2,φ(b)=8;φ(c)=4,φ(a)=4,φ(b)=4;φ(c)=4,φ(a)=8,φ(b)=2;φ(c)=4,φ(a)=16,φ(b)=1。 1)当φ(c)=4,φ(a)=1,φ(b)=16时,c=5,8,10,12;a=1,2;b=17,32,34,40,48,60。将a,b,c分别组合代入(a,bc)=1,(b,c)=1经验证得(a,b,c)=(1,17,5),(1,17,8),(1,17,10),(1,17,12),(1,32,5),(1,34,5),(1,48,5),(2,17,5)满足(1)式。 2)当φ(c)=4,φ(a)=2,φ(b)=8时c=5,8,10,12;a=3,4,6;b=15,16,20,24,30。将a,b,c分别组合代入(a,bc)=1,(b,c)=1经验证得(a,b,c)=(3,16,5)满足(1)式。 3)当φ(c)=4,φ(a)=4,φ(b)=4时a=b=c=5,8,10,12。将a,b,c分别组合代入(a,bc)=1,(b,c)=1,经验证不存在(a,b,c)满足(1)式。 4)当φ(c)=4,φ(a)=8,φ(b)=2时c=5,8,10,12;a=15,16,20,24,30;b=3,4,6。将a,b,c分别组合代入(a,bc)=1,(b,c)=1,经验证得(a,b,c)=(16,3,5)满足(1)式。 5)当φ(c)=4,φ(a)=16,φ(b)=1时c=5,8,10,12;a=17,32,34,40,48,60;b=1,2。将a,b,c分别组合代入(a,bc)=1,(b,c)=1,经验证得(a,b,c)=(17,1,5),(17,1,8),(17,1,10),(17,1,12),(17,2,5),(32,1,5),(34,1,5),(48,1,5)满足(1)式。 (2)当φ(c)=5,φ(a)φ(b)=10时,得φ(c)=5,φ(a)=1,φ(b)=10;φ(c)=5,φ(a)=2,φ(b)=5;φ(c)=5,φ(a)=5,φ(b)=2;φ(c)=5,φ(a)=10,φ(b)=1。由引理3知φ(c)=5无解,因此式(1)无解。 (3)当φ(c)=6,φ(a)φ(b)=8时,得φ(c)=6,φ(a)=1,φ(b)=8;φ(c)=6,φ(a)=2,φ(b)=4;φ(c)=6,φ(a)=4,φ(b)=2;φ(c)=6,φ(a)=8,φ(b)=1。 1)当φ(c)=6,φ(a)=1,φ(b)=8时,c=7,9,14,18;a=1,2;b=15,16,20,24,30。 将a,b,c分别组合代入(a,bc)=1,(b,c)=1,经验证得(a,b,c)=(1,15,7),(1,16,7),(1,20,7),(1,24,7),(1,30,7),(1,16,9),(1,20,9),(1,15,14),(2,15,7)满足(1)式。 2)当φ(c)=6,φ(a)=2,φ(b)=4时,c=7,9,14,18;a=3,4,6;b=5,8,10,12。将a,b,c分别组合代入(a,bc)=1,(b,c)=1,经验证得(a,b,c)=(3,5,7),(3,8,7),(3,10,7),(3,5,14),(4,5,7),(4,5,9),(6,5,7)满足(1)式。 3)当φ(c)=6,φ(a)=4,φ(b)=2时,c=7,9,14,18;a=5,8,10,12;b=3,4,6。 将a,b,c分别组合代入(a,bc)=1,(b,c)=1,经验证得(a,b,c)=(5,3,7),(5,6,7),(8,3,7),(10,3,7),(5,3,14),(5,4,7),(5,4,9)。 4)当φ(c)=6,φ(a)=8,φ(b)=1时,c=7,9,14,18,a=15,16,20,24,30,b=1,2。 将a,b,c分别组合代入(a,bc)=1,(b,c)=1,得(a,b,c)=(15,1,7),(15,1,14),(15,2,7),(16,1,7),(16,1,9),(20,1,7),(20,1,9),(24,1,7),(30,1,7)。 (4)当φ(c)=7,φ(a)φ(b)=7时,得φ(c)=7,φ(a)=1,φ(b)=7;φ(c)=7,φ(a)=7,φ(b)=1。由引理3知φ(c)=7 无解,因此式(1)无解。 (5)当φ(c)=9,φ(a)φ(b)=6时得,φ(c)=9,φ(a)=1,φ(b)=6;φ(c)=9,φ(a)=2,φ(b)=3;φ(c)=9,φ(a)=3,φ(b)=2;φ(c)=9,φ(a)=6,φ(b)=1。由引理3知φ(c)=9无解,因此式(1)无解。 (6)当φ(c)=15,φ(a)φ(b)=5时得,φ(c)=15,φ(a)=1,φ(b)=5;φ(c)=15,φ(a)=5,φ(b)=1。由引理3知φ(c)=15无解,因此式(1)无解。 (1)当φ(c)=2,φ(a)φ(b)=8时得,φ(c)=2,φ(a)=1,φ(b)=8;φ(c)=2,φ(a)=2,φ(b)=4;φ(c)=2,φ(a)=4,φ(b)=2;φ(c)=2,φ(a)=8,φ(b)=1。 1)当φ(c)=2,φ(a)=1,φ(b)=8时,c=3,4,6;a=1,2;b=15,16,20,24,30。将a,b,c分别组合代入上述4种关系逐一验证得(a,b,c)=(2,15,4),(2,16,3),(2,20,3),(1,16,4),(1,20,4),(1,24,4)满足(1)式。 2)当φ(c)=2,φ(a)=2,φ(b)=4时,a=c=3,4,6;b=5,8,10,12。将a,b,c分别组合代入上述4种关系逐一验证得(a,b,c)=(4,5,6),(4,10,3),(3,10,4),(3,8,4),(4,5,4),(4,8,3)满足(1)式。 3)当φ(c)=2,φ(a)=4,φ(b)=2时,c=b=3,4,6;a=5,8,10,12。将a,b,c分别组合代入上述4种关系逐一验证得(a,b,c)=(10,3,4),(10,4,3),(5,4,6),(5,6,4),(5,4,4),(8,3,4),(8,4,3)满足(1)式。 4) 当φ(c)=2,φ(a)=8,φ(b)=1时,c=3,4,6;a=15,16,20,24,30;b=1,2。将a,b,c分别组合代入上述4种关系逐一验证得(a,b,c)=(30,1,4),(16,1,6),(20,1,6),(16,2,3),(20,2,3) (15,2,4),(16,1,4),(20,1,4),(24,1,4)满足(1)式。 (2)当φ(c)=3,φ(a)φ(b)=4时,即φ(c)=3,φ(a)=1,φ(b)=4;φ(c)=3,φ(a)=2,φ(b)=2;φ(c)=3,φ(a)=4,φ(b)=1,由引理3知φ(c)=3无解,因此式(1)无解。 当φ(c)=1,φ(a)φ(b)=4时,φ(c)=1,φ(a)=1,φ(b)=4;φ(c)=1,φ(a)=2,φ(b)=2;φ(c)=1,φ(a)=4,φ(b)=1。 1)当φ(c)=1,φ(a)=1,φ(b)=4时,c=a=1,2;b=5,8,10,12,将a,b,c分别组合代入上述三者逐一验证得(a,b,c)=(2,8,2),(2,10,2),(2,12,2)满足(1)式。 2)当φ(c)=1,φ(a)=φ(b)=2时,c=1,2;a=b=3,4,6,将a,b,c分别组合代入上述三者逐一验证得(a,b,c)=(4,4,2),(4,6,2),(6,4,2)满足(1)式。 3)当φ(c)=1,φ(a)=4,φ(b)=1时,c=b=1,2;a=5,8,10,12,将a,b,c分别组合代入上述三者逐一验证得(a,b,c)=(10,2,2),(12,2,2),(8,2,2)满足(1)式。 综上所述,该定理得证,即有本文结论。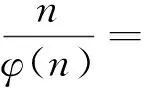

2 定理及其证明