蝗虫优化算法求解跳-扩散模型参数估计问题

倪百秀，刘长平，李国成*

(1.皖西学院 金融与数学学院，安徽 六安 237012；2.淮阴工学院 管理工程学院，江苏 淮安 223200)

0 引言

金融市场经常会受到政治、经济和社会的突发事件等信息冲击而造成资产价格的异常变动，学者们称之为资产价格跳跃行为。Press[1]将跳跃因子加入到扩散模型，构建复合事件模型，用于刻画金融资产的价格过程。Merton[2]将跳跃过程引入到连续的随机过程提出基于过程的期权定价模型，对著名的Black-Scholes期权定价公式进行了完善，开启了期权定价模型研究的新篇章。Kou[3]提出了非对称的双指数跳-扩散模型，具体刻画了金融资产收益的概率分布的尖峰和厚尾等特征，合理地解释了“波动微笑”现象。沈根祥[4]采用时点方差估计方法构建跳检验统计量并对沪深300指数进行检测，证实了跳的存在性，且跳的次数服从Poisson过程。黄苒和唐齐鸣[5]利用可变强度跳跃-GARCH模型来研究资产价格跳跃行为，刘杨树等[6]利用多维跳跃扩散模型来研究跳跃风险对期权复制收益的影响，巢文等[7]采用双指数跳跃扩散模型对长寿债券定价进行研究，宫晓莉等[8]基于广义双指数分布的跳跃扩散模型研究股指期货的波动。

尽管跳-扩散模型的理论和实证研究已取得了丰硕的成果，但是其参数估计问题仍是一个极具挑战性的问题。Fortune[9]采用极大似然估计法和迭代搜索实现对MERTON模型的参数估计，并对S&P500等5个股票指数进行实证研究。AIT-sahalia[10]分别采用矩估计法和极大似然估计法来对MERTON模型的参数进行近似估计。Ramezani等[11]借助Pareto和Beta分布组合双指数跳-扩散模型下的资产收益的概率分布，并借助极大似然估计法实现模型参数的估计。吕韩等[12]通过构建一种新的跳跃识别方法，采用平滑技术实现对跳跃频率的估计，进而实现双均匀模型参数估计。从目前研究成果来看，极大似然估计法较为适合模型的参数估计[10]。但其困难在于其相应的似然函数较为复杂，基于梯度的经典优化方法已不再适用。为此，本文探寻用基于群体智能的蝗虫优化算法(Grasshopper Optimization Algorithm, GOA)[13]来求解该似然函数最大化问题，进而实现跳-扩散模型的参数估计，并进行实证研究。

1 问题描述

1.1 数学模型

假设金融市场有n个风险资产(股票)可供交易，设t时刻资产(股票)i价格为Si(t),i=1,2,…,n,t∈[0,T]，其满足以下方程：

(1)

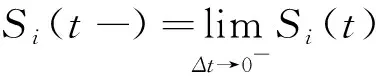
将研究时间段等间隔离散化，为简便起见，不妨记为t=0,1,2,…,T，则离散形式的资产价格过程为：

Si(t+Δt)=

(2)

其相应的离散化的对数价格过程为：

(3)

1.2 跳-扩散模型参数估计问题

模型参数的估计方法主要有极大似然估计(Maximum likelihood estimation, MLE)、广义矩估计(Generalized method of moments, GMM)、模拟矩估计(Simulated moment estimation, SME)和MCMC方法[10]。文献[10]的研究结果表明极大似然估计最适合模型的参数估计。文献[9]给出了(3)式所描述的离散化对数价格过程的对数似然函数，具体如下：

(4)

(5)

经典的优化方法如基于梯度的优化算法等都难于对式(5)所描述的无约束优化问题进行求解。为此，本文探寻用蝗虫优化算法来直接对其进行随机搜索求解。

2 蝗虫优化算法

2.1 算法思想

蝗虫优化算法是由Saremi等(2017)[13]通过构建数学模型来模拟蝗虫群的移动而提出的一种新型仿生群智能算法。该算法在函数优化[13]、工程优化[13]、多目标优化[14]、特征提取[15]等方面都取得了很好的应用效果。

设popi为蝗虫群中第i个蝗虫的位置，由蝗虫群个体间的作用力、重力以及风力的共同决定的，其数学描述如下[13]：

popi=Si+Gi+Ai,i=1,2,…,N

(6)

(7)

(8)

其中f和l是表示蝗虫群间相互吸引力强度和距离长度的参数。

为了求解优化问题，Saremi等(2017)[13]对(6)式进行改进：

i=1,2,…,N

(9)

(10)

M为最大迭代次数，m为当前迭代次数，cmax和cmin为收缩因子的最大值和最小值。

2.2 算法步骤

蝗虫优化算法的主要步骤描述如下：

Step1确定搜索空间，初始化基本参数，随机生成初始种群。

Step2评估初始种群，确定当前最优解和最优值。

Step3按式(10)更新收缩因子c。

Step4计算所有蝗虫间距dij，按式(9)更新每只蝗虫的位置，并进行可行性检测。

Step5评估种群，更新当前最优解和最优值。

Step6检查迭代的终止条件。若不满足，则转向Step3；否则终止迭代，输出最优解和最优值。

2.3 适应度函数

设种群中个体数为N，则每个个体popi代表模型的一组参数(μ,σ,λ,μJ,σJ)。由式(5)所描述的最优化问题可定义蝗虫优化算法求解跳-扩散模型参数估计问题的适应度函数如下：

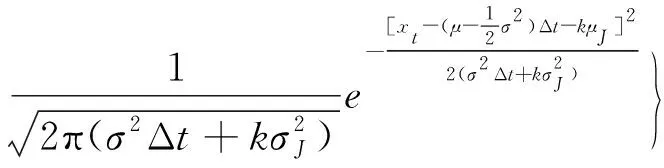
(11)

由此，利用资产价格历史数据计算得到对数价格增量序列xt=lnSt-lnSt-1,t=1,2,…,T，进而利用蝗虫优化算法即可获得资产价格模型参数的极大似然估计值和最优参数。

3 数值实验和结果分析

3.1 样本数据的选取与统计特征

本文从全球金融市场中选取中国上证综指(SSECI)、中国香港恒生指数(HSI)、日本日经指数(Nikkei225)、美国标准普尔500指数(S&P500)、英国富时100指数(FTSE100)和德国综合指数(DAX)等6个市场指数来进行实证研究，历史数据来源于雅虎财经，每个指数采样为2016年1月1日到2018年6月30日的收盘价，有效样本数据个数分别为607、612、614、628、630和632，如图1所示，本文取每个市场的2016和2017年数据作为训练样本，用于估计模型参数，2018年数据作为测试数据。

6个市场指数样本数据日收益率的基本统计特征如表1所示，同时为了进一步检验日收益率是否服从正态分布，采用Jarque-Bera检验法进行检验，即在给定显著性水平α=0.01下，分别计算出J-B统计量的值和接受正态分布假设的概率P。

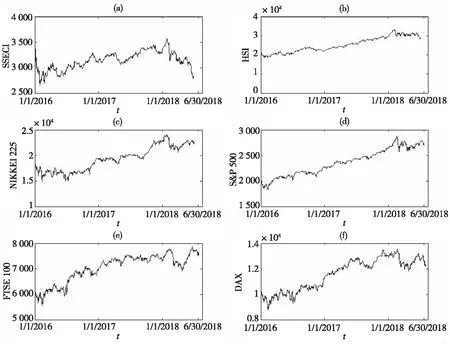
图1 6个市场指数日收盘价变化趋势图Fig.1 Daily closing price trends of six indexes

表1 6个市场指数日收益率的统计特征和J-B检验结果Tab.1 Statistical characteristics of daily returns and results of J-B test of six indexes

首先，从表1可以看出6个市场指数日收益率样本数据的峰度(Kurtosis)的最小值为4.548 8，最大值为10.006 0。由统计学知识可知正态分布的峰度值为3，若峰度值大于3，则样本数据分布表现为尖峰性(比正态分布凸起程度大)。由此可知6个市场指数日收益率样本数据分布均具有尖峰性。其次，表1中6个市场指数日收益率样本数据的偏度(Skewness)的最小值为-1.142 4，最大值为-0.005 4，均小于零。样本数据分布具有负偏离，即左偏态，即体现了厚尾分布的特征。最后，为进一步检验6个市场指数日收益率样本数据是否服从正态分布，本文在给定显著性水平α=0.01下进行了Jarque-Bera检验，表1中的检验统计量J-B的值都很大，其中最小值为91.57，最大值为1 651.77，99%的置信水平下接受正态分布假设的概率P值均小于0.000 1(以0.000计)，亦即在99%的置信水平下几乎以概率1拒绝正态分布假设。为了更为直观地展示这一特点，图2给出6个市场指数日收益率样本数据的正态分布检验Q-Q图，进一步佐证了6个市场指数日收益率样本数据不服从正态分布。依据峰度和偏度的统计意义和表中的数值以及Jarque-Bera检验的结果可以表明6个市场指数日收益率样本数据均具有尖峰厚尾的特性，而不服从正态分布，这与金融时间序列数据分布的特性相一致，也正是跳-扩散模型提出和广为接受的根本原因，因而本文假设资产价格路径服从跳-扩散模型是合理和恰当的。

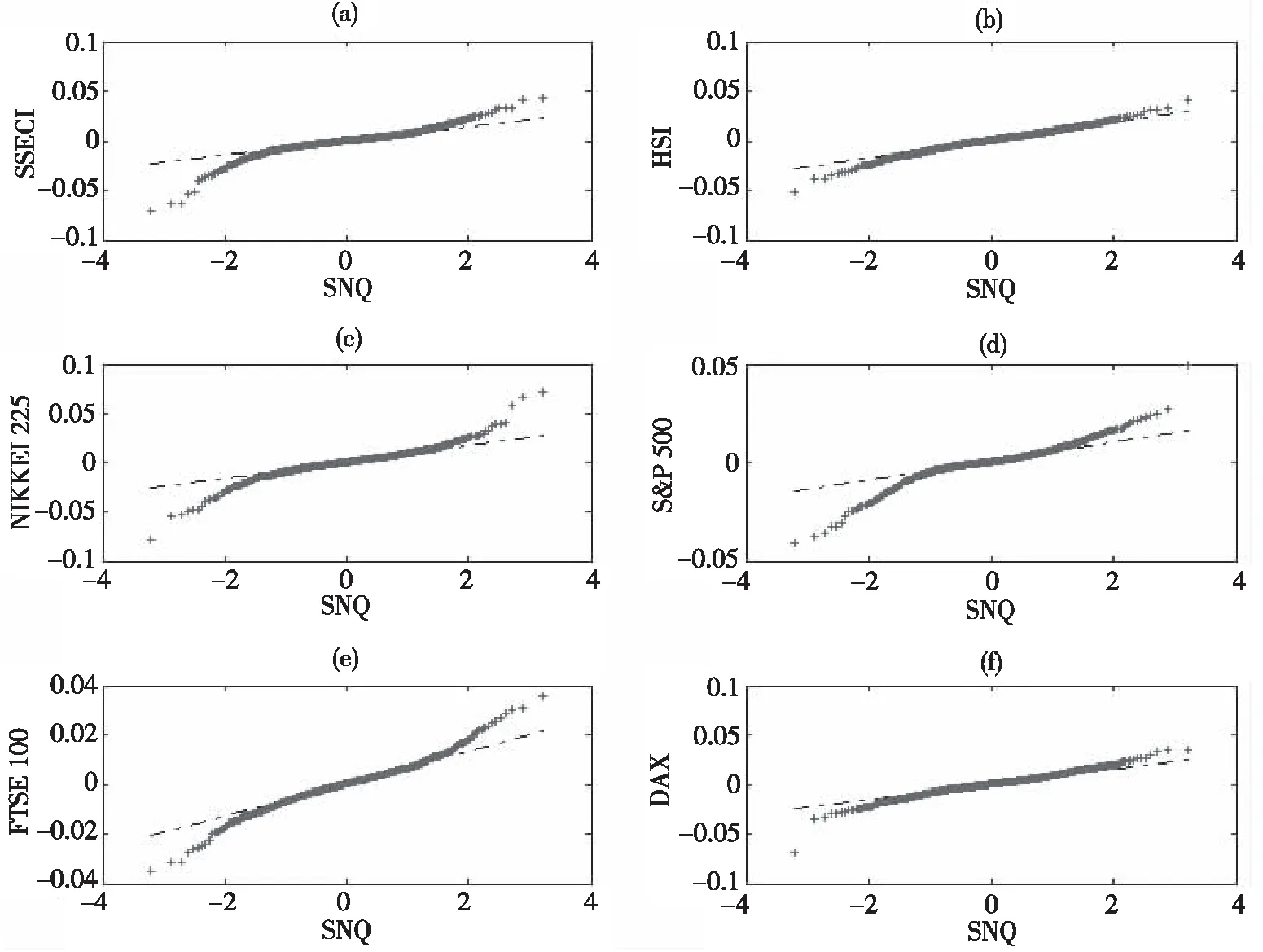
图2 6个市场指数日收益率的Q-Q图Fig.2 Q-Q chart of daily returns of six indexes

3.2 参数估计结果

借助于极大似然估计法和蝗虫优化算法分别对基于市场指数两年的对数日收益率样本数据实现模型参数估计。由于采用的是日收盘价时间序列，因而式(5)中k的取值为0或1，即每天最多只产生1次跳跃，每个市场指数的模型参数估计实验均独立运行30次，结果如表2所示。

表2 6个市场指数的模型参数估计结果Tab.2 The results of model parameter estimation of six indexes

3.3 结果分析与检验

表2借助于MLE获得6个市场指数价格路径服从模型的参数，在此基础上可以利用Kolmogorov-Smirnov单样本检验(K-S检验)来实现资产价格服从模型这一假设的合理性以及模型参数估计的准确性检验。如前所述每个股票指数用于模型参数估计的样本内数据个数分别为487、490、492、502、504、506个(对数日收益率)，用于测试的样本数据个数分别为242、244、245、249、252、250个(对数日收益率)。K-S检验中的理论分布函数F0(x)即为所估计的模型参数确定的对数日收益率的分布函数，其密度函数如下所示：

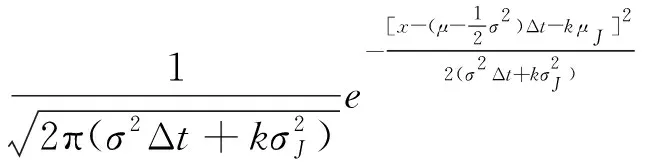
(12)

因而，对于给定的模型参数(μ,σ,λ,μJ,σJ)，其相应的理论分布函数F0(x)可表示为：

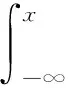
(13)

K-S检验统计量定义如下：

(14)

式(14)所描述的K-S检验统计量表达式中的F0(x)可以借助Matlab软件中的积分函数@quad1进行计算，其中样本数据的累计频数分布Fn(x)可以借助Matlab软件中的@tabulate和@cumsum加以计算。由于检测中的样本内数据个数和样本外数据个数均大于50，因而其临界值的计算式采用：

(15)

6个市场指数模型的K-S检验结果如表3所示，其中置信水平为95%(σ=0.05)。

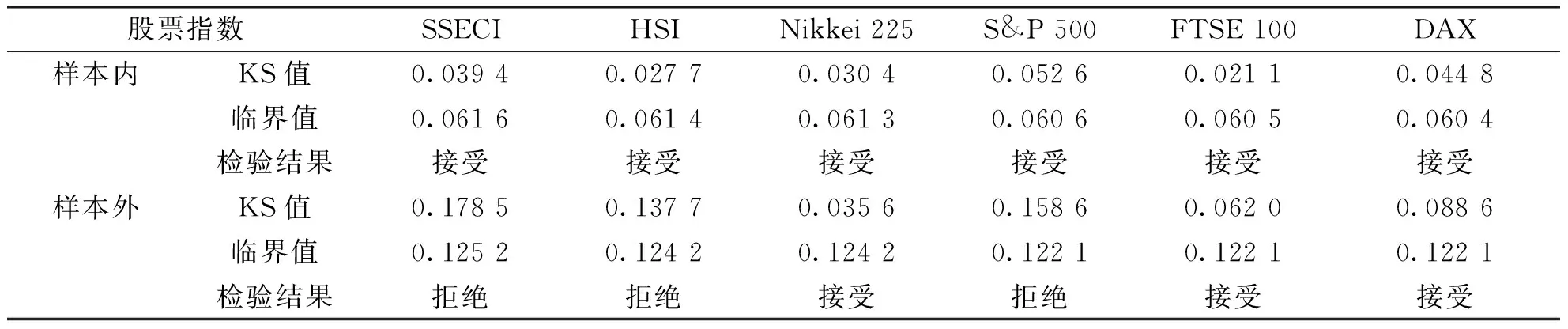
表3 6大市场指数的价格路径模型K-S检验结果Tab.3 K-S test results of price path models of six indexes

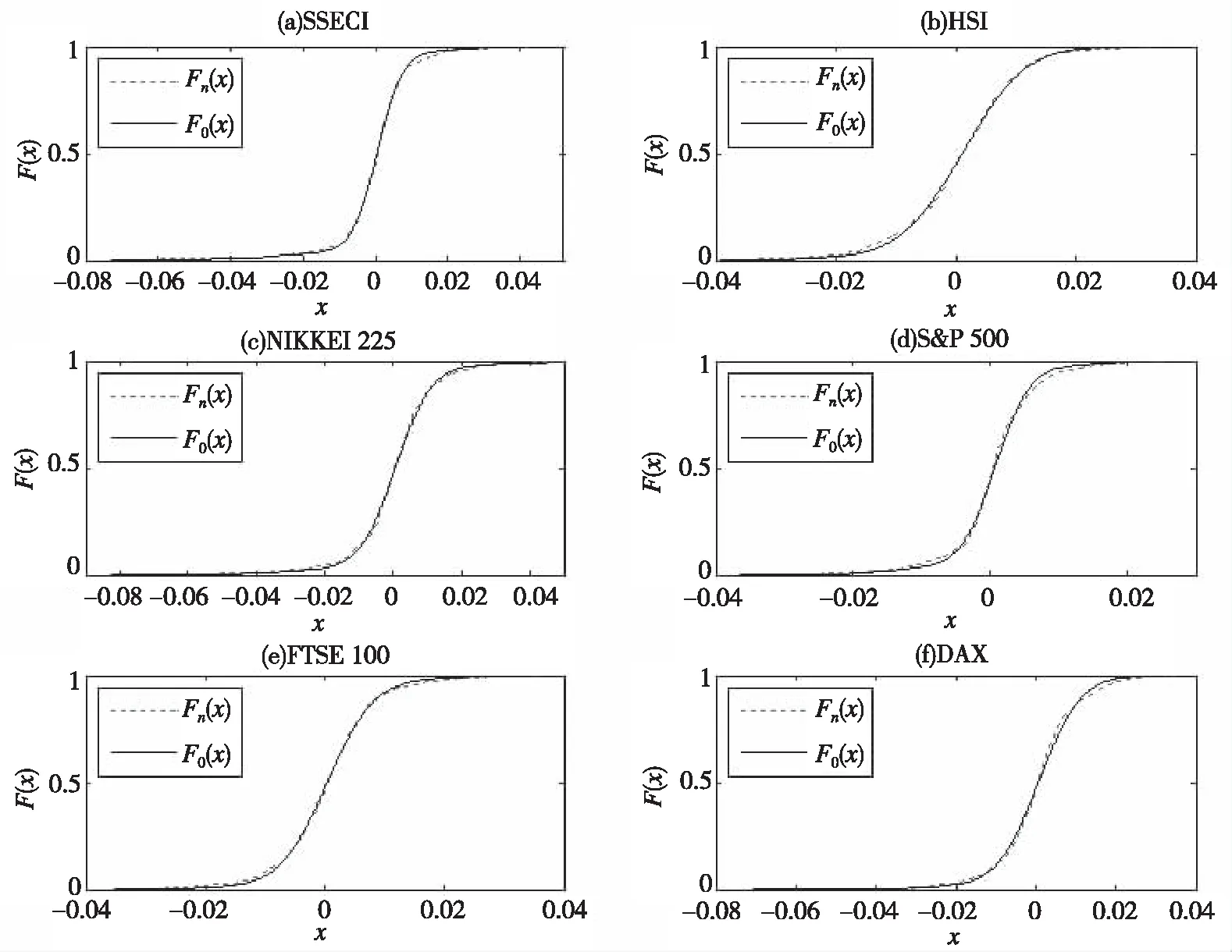
图3 理论分布函数和样本内数据累计频数分布对比Fig.3 Comparison of theoretical distribution function and cumulative frequency distribution of data in samples

图4 理论分布函数和样本外数据累计频数分布对比Fig.4 Comparison of theoretical distribution function and cumulative frequency distribution of out-of-sample data

表3的K-S检验结果表明，基于样本内数据的6个市场指数的价格路径模型假设合理，模型参数估计准确。对于Nikkei225、FTSE100和DAX三个指数而言把样本内数据估计模型参数的结果推广到样本外仍然是准确的，但对于SSECI、HSI和S&P500三个指数而言样本外数据的验证就出现一些偏差。这主要是因为2018年的1月底至2月初全球股市因系统风险而产生暴跌，而后Nikkei225、FTSE100和DAX三个指数逐渐回升，而3月份开启中美贸易战使得HSI和S&P500两个指数虽然逐渐回升但市场波动较大，同时国内的去杠杆、信用风险全面爆发以及中美贸易战的加剧等因素使得SSECI持续下跌。从图1也可清楚地观察到6个市场指数的样本内外的异同。

为了更为直观地体现模型假设的合理性和参数估计的准确性，图3和图4分别给出6个市场指数的理论分布函数和样本内数据累计频数分布以及样本外数据累计频数分布的图形对比。从图3可以看出6个市场指数的理论分布函数和样本内数据累计频数分布都非常吻合，拟合优度高，其中最好的是HSI和FTSE100，这也从表3加以印证，表3中这两个市场指数的检验统计量KS值都很小，吻合度最差的S&P 500指数，其对应表3中统计量的值也是最大的。

对比图3和图4可以看出6个市场指数的理论分布函数和样本外数据累计频数分布拟合优度比样本内数据都差，而且差距明显，其中最好的是Nikkei225，其次是FTSE100和DAX，SSECI、HIS和S&P500三个指数的拟合优度较差。

4 结论

本文将蝗虫优化算法应用于基于极大似然估计法的跳-扩散模型参数估计问题的求解。首先借助于极大似然估计法将跳-扩散模型参数估计问题转化成一个非线性优化问题，然后雇用蝗虫优化算法这一基于仿生学的群智能算法来实现该优化问题的求解，最后选取美国标准普尔500指数等全球六大证券市场指数来进行实证研究，并用K-S检验对模型参数估计结果进行检验，结果表明蝗虫优化算法求解模型参数估计问题是可行和有效的，为跳-扩散模型在金融领域的应用提供了一定的技术支撑。