用“差异取值验证法”巧解高考数学选择压轴题
2020-09-11刘欣华
●刘欣华
高考数学选择题近年来一直稳定在12个小题,每个小题5分;考查内容覆盖范围广,穿插多个知识点的链接,融入多种数学思想和方法。考生必须具备快速、有效的基本解题技巧和能力。这不但是教学过程的重点,而且也是教学成果的体现。因此,研究高考数学选择题的解题技巧具有重大的现实意义。
一、高考数学选择题解题技巧概述
高考数学选择题根据考试大纲,一般情况下按由易到难的顺序排列,主要考点分A、B、C三级。A级是基础的题目,能力要求为“了解、理解”,B级主要是中档题目,能力要求为“理解、掌握”,C级为难题、压轴题,能力要求为“综合应用”。考生需要发挥双向思维,充分利用题设和选项两个方面所提供的已知信息进行解题,通过多种解题技巧迅速完成,一般情况下每个题至少有两种或两种以上的解题方法。
高考数学选择题的解题技巧要注意避免复杂的大量计算,避免常规的解题方法。大多数选择题可以运用常见的解题技巧:直接法、代入验证法、分析排除法、估值推算法、特殊取值法、图解法。但是最后两道压轴题题型复杂,信息量大,费时费力,需要运用特殊的解题技巧才能迅速排除干扰项:单选题模式固定,结构独特,在有限的备选答案中,仅有一个是正确的;依据选项彼此之间相近又相互排斥的特点,可以采用差异取值验证法求解。
二、差异取值验证法的思维原理和适用范围
“差异取值验证法”是根据选择题的备选项,观察每个选项区间范围和差异,代入差异的特殊值验证是否符合题设条件从而进行取舍。其适用范围——适用于选择题;选择题的选项中含有区间范围。具体分三个步骤:第一步是找选项中的“差异”;第二步“取值”,通过选项中的差异出现的值,而且一定是特殊值;第三步“验证”,验证题目中给的等式或者不等式是否成立。
这种解题思想突破常规技巧,巧妙地避开了难点,节省书写解题过程所耗用的时间,使考生体会到“柳暗花明”,凸显其准确、迅速判断答案的优势;检验考生的观察能力和发散性思维;逐步提升考生的数学思维层次以及分析、判断和推理问题的能力。
三、差异取值验证法在高考数学选择题中的具体应用
(一)问题初阶,掌握基本思想

分析:此题是选择题,而且选项给出区间,可以采用差异取值验证法。
对比选项之间的差异,在四个选项中,0都不在范围内,因此0不作为特殊值考虑。而选项A、D含有-1,选项B、C不含有-1,这时取特殊值-1.①当x=-1时,f(0) 例2定义在[-2,2]上的函数f(x)满足(x1-x2)[f(x1)-f(x2)]>0,x1≠x2且f(a2-a)>f(2a-2),则实数a的取值范围为() A.[-1,2]B.[0,2)C.[0,1)D.[-1,1) 分析:由已知条件判定此函数为单调递增函数。此选择题给出了选项范围,考虑差异取值验证法。 观察选项中的特殊值,每个选项都含0,因此不作为特殊值考虑。选项A、D含有-1,B、C不含有-1,这时取特殊值-1。①当a=-1时,得f(2)>f(-4),已知函数的定义域是[-2,2],显然不符合,说明a不能取-1,排除选项A、D。 再对比选项B、C的差异,两个选项都含0,选项B含有1,选项C不含1,这时取特殊值1。②当a=1时,则f(0)>f(0),显然不成立,a不含1,排除选项B,答案选C。 例1、例2中一般的函数图像法和单调性可以求解,只是稍显麻烦,通过差异取值验证法只需要验证两步就得出结论,运算量非常小,简单有效。 例3已知函数f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则实数a的取值范围是() A.(-1,2)B.(-∞,-3)∪(6,+∞)C.(-3,6)D.(-∞,-1)∪(2,+∞) 分析:考查极大值和极小值问题就涉及到了导数,涉及到了单调性,说明导数有正有负,原函数有增有减。因此先求导数f'(x)·=3x2+·2ax+a+6 观察四个选项中,A、C选项含有0,B、D选项不含有0,这时取特殊值0。①令a=0时,f'(x)·=3x2+6>0则f(x)递增,这与已知函数有极小值不符,因此a不能取0,排除选项A、C 再对比选项B、D的差异,取特殊值-2。②令a=-2时,f'(x)·=3x2-4x+4,判别式△=16-3×16<0,则f'(x)>0恒成立,这时f(x)是递增函数,与已知相悖,故排除含有-2的选项D,答案选B。 具备了差异取值验证法的思维和方法后,通过观察,在不同区间和范围内选取合适的差异特殊值,可以轻松自如地解决高考中的压轴题 例5(2014全国卷11题)若函数f(x)=kx-lnx在区间(1,+∞)单调递增,则k的取值范围是() 分析:由已知条件考察函数的单调性涉及导数,依据函数在区间上单增,可知导数 观察四个选项都不含有0,第一步比较A、B选项的差异,取特殊值-1,①令k=-1时,原式化为,由x∈(1,+∞),显然不成立,排除含有-1的选项B,再令k=-2,原式化为由x∈(1,+∞),亦不成立,同理排除选项A。 第二步在选项C、D中,取差异值1,②令k=+1时,原式化为,由x∈(1,+∞),恒成立。故选择含有1的选项D,答案为D。 注:此题在寻求选项的差异时,观察到A、B、C选项均不含有1,选项D含1,不妨直接选取差异特殊值1。令k=1时,得1≥,一定成立,因此可直接判断答案D。 分析:本题考查函数的奇偶性和单调性,常规方法把此问题转化为|x|>|2x-1|,平方化为x2>(2x-1)2,求解不等式。 用差异取值验证法只需两步:第一步观察选项A、C和B、D的差异,选取特殊值0。①令x=0时,原式化为f(0)>f(-1),即,即-1>ln2-0.5,显然不成立,故排除含有0的选项A、C。 第二步取选项B、D的差异值1.②令k=1时,原式化为f(1)>f(1),显然不成立,故排除含1的选项D,答案选B。 例7(2018全国卷市级统考)已知函数f(x)=-x3+3x2-mx-2m,若存在唯一的正整数x0,使得f(x0)>0,则m的取值范围是() 第二步在选项C、D中取差异特殊值1.②令m=1时,原式化为f(x)=-x3+3x2-x-2=-x2(x-3)-(x-2),对于上式当x>3时,f(x)<0恒成立,因此只需验证x=1、2、3时,这时f(1)=-1+3-1-2=-1<0,f(2)=-8+12-2-2=0,f(3)=-27+27-3-2=-5<0,故不埚正整数x0,使得f(x0)>0。综上所述m=1时不成立,排除含有m=1的选项D,答案选C。 如何恰当地选取合适的差异特殊值,既是运用差异取值验证法的关键,也是处理这类问题的难点,需要考生反复练习,增强观察明锐性和分析问题的能力 相对于传统的数学选择题解题技巧,差异取值验证法是在综合的方法的基础上,充分挖掘题目的个性特征,整体分析,横向比较,巧妙排除,规避难点,探寻简便解法;是考生取得高考数学优异成绩的重要保证。(二)问题升华,巧妙选取差异特殊值
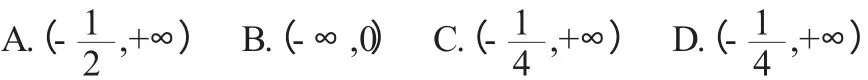
(三)问题精进,综合分析高考选择题



四、结论
