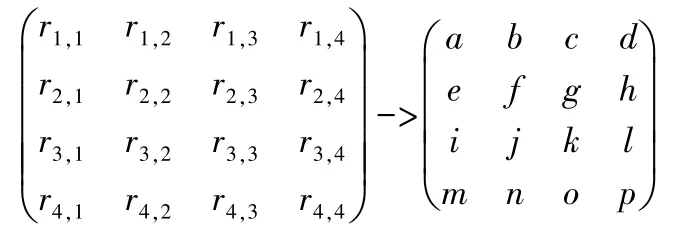Sweedler 代数上的 Rota⁃Baxter 代数

◎郝午牛 刘春麟 解瑞明 陈全国 （曲阜师范大学数学科学学院，山东 曲阜 273165）

一、引言

为了解决分析和组合问题，Rota⁃Baxter 算子被引入［1－3］，其在数学和数学物理领域中有重要的应用.文［4］给出了二维复预李代数上的所有 Rota⁃Baxter 算子； 文［5］几乎给出了三维复结合代数上所有Rota⁃Baxter 算子.

设A为域F上的结合代数，R：A→A是线性算子 如果

R（x）R（y）＋λR（xy）＝R（R（x）y）＋R（xR（y）），x，y∈A，

其中λ∈F是任意给定纯量，那么称R是A的一个权λ的 Rota－Bxter 算子.显然，对任意λ≠0，λ－1R是权为 1 的Rota⁃Baxter 算子.

文中，我们欲讨论四维 Sweedler 代数上的 Rota⁃Baxter算子，采用数学软件Mathematica 进行编程，计算出Sweedler代数上的所有 Rota⁃Baxter 算子，区别于以往文献［6－7］的算法，提供了利用计算机编程计算有限维代数上所有Rota⁃Baxter 的新方法.

二、主要结论

本节，我们主要讨论以x，g为生成元，且满足条件：x·x＝0 ，g·g＝1 ，x·g＝－g·x的 Sweedler 代数（A，·）.令α，β∈A，且α，β在基 1，x，g，x·g下的坐标分别为（α1α2α3α4）′和（β1β2β3β4）′，则αβ可用“拟二次型”来表示，即

以下固定生成元“基底”1，x，g，x·g，把α在生成元“基底”下坐标与α等同看待，并记B（i）＝ （δji）4×1（i＝ 1，…，4）为第i个生成元在基下的坐标，特别地，记B（5）＝ （0）4×1为（A，·）中零元在“基底”下的坐标.在 Mathematica 中，为方便编码及计算机识别，在代码中，用ε，ϕ，φ，ψ依次代替1，x，g，x·g，用θ代指（A，·）中的零元.

对应Mathematica 代码如下：

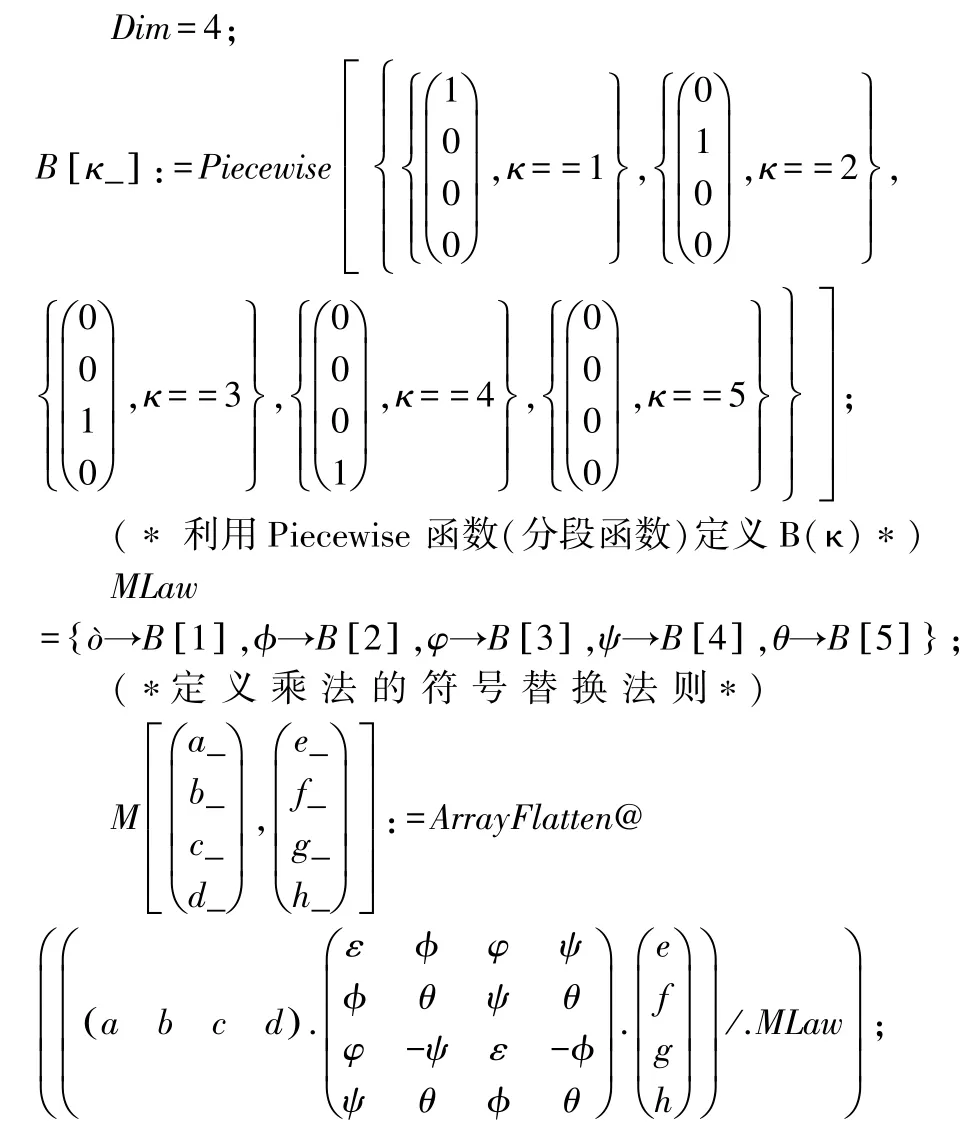
（∗利用Mathematica 的符号化运算计算拟二次型的运算结果，并对无实际定义的符号进行替换，对最终结果以延迟赋值的形式赋值给函数M作为乘法函数∗）

设R∈End（A），令R在基 1，x，g，x·g下的表示矩阵

则R（α）在基 1，x，g，x·g下坐标为：

对应Mathematica 代码如下：

（∗定义R在生成元 1，x，g，x·g下的表示矩阵为RM∗）

（∗求以（s，t，u，v）为坐标的元素在自同态R下作用所得到的像的坐标，并把该坐标以延迟赋值的形式赋值给函数R作为自同态R的表示函数∗）.

定理 1 设α，β∈（A，·），R∈End（A），令α，β在基 1，x，g，x·g下的坐标分别为(α1α2α3α4) ′和(β1β2β3β4)′，则元素

R（α）·R（β）＋λR（α·β）－R（R（α）·β）－R（α·R（β））

在基 1，x，g，x·g下的坐标可通过 Mathematica 计算得出，Mathematica 代码如下：

（∗此为Rota⁃Baxter 条件的表示函数∗）

（∗此为当α为第i个生成元、β为第j个生成元时，所对应的Rota⁃Baxter 条件的表示函数∗）

我们针对λ＝ 0 的解进行讨论，设α，β∈（A，·），R∈End（A），则当α，β遍历生成元时，将对应 Rota⁃Baxter 条件的坐标表达式合并，即可得到表达式集合，对表达式集合进行修改即可得到约束条件方程组，使用Reduce 函数对方程组进行约化，即可得到对应解的所有情况，即满足Rota⁃Baxter 条件的所有自同态解.

（∗此为遍历生成元所有组合后得到的所有的Rota⁃Baxter 条件表达式所构成的集合∗）

（∗此为遍历生成元所有组合后得到的所有的Rota⁃Baxter 条件所构成的集合，即Rota⁃Baxter 约束条件的方程组∗）

Reduce[AE].

（∗通过Reduce 函数对方程组进行约化，从而得出解的所有可能情况，即满足Rota⁃Baxter 条件的所有自同态解∗）

当λ＝ 0 时，程序运行后，得到所有满足 Rota⁃Baxter 等式情况及其所对应的矩阵.

为方便表示，下用字母来替代对应ri，j并用字母矩阵进行解的坐标表示，替代规则如下：