浅谈数学归纳法在中学数学中的应用
2020-09-11李英爽北华大学数学统计学院吉林吉林132013
◎李英爽 郭 微 (北华大学数学统计学院,吉林 吉林 132013)
数学归纳法表面看着很简单,形式固定,但是很多学生难以理解其本质.有的同学在使用数学归纳法时完全靠生硬的记忆,不能掌握其真正的思想.那么,应该怎样理解数学归纳法的主要思想,解决问题时数学归纳法分哪几步,在中学数学中它都有哪些应用? 本文就是在理解数学归纳法的概念,了解数学归纳法解题步骤的基础上,论述数学归纳法在中学数学中的主要应用,帮助学生使用数学归纳法证明一些复杂的命题.
一、数学归纳法的概念
数学归纳法是一种数学证明方法,主要用于证明某个命题在自然数范围内成立.在自然数之外的一些数学定理的证明也可以使用数学归纳法.数学归纳法在中学数学中是一种比较严谨的推理方法,主要用来解决与整数相关的数学问题,如证明一些等式和公式成立.
二、数学归纳法的步骤
数学归纳法在应用时分两步进行:
第一步,证明命题在常数的情况下成立.从数学的角度看,命题在常数的情况下成立,那么命题在特殊的情况下也成立,这是证明命题成立的基础,是最基本的步骤,在实际解决问题中,通常用“1”作为证明命题的起点.
第二步,证明命题在任意常数下都成立.在实际解决问题中,我们通常采用未知数k来代表一般情况.在n=k的情况下命题成立,然后推导出n=k+1 的时候命题也成立.这是证明命题成立关键的一步,同时它也代表着所要证明的结论具有普遍性.在归纳分析的时候,要将特殊的情况推广到一般的情况才能证明命题的正确.
总的来说,数学归纳法的基本思路就是通过归纳总结来证明命题的成立.数学归纳法的第一步是很容易进行验证的,就是证明命题在特殊情况下成立.但归纳法的第二步是有点难度的,也是最核心的步骤.利用数学归纳法证明命题时,只有在这两步同时成立的情况下,才能证明命题正确.下面我们来探讨一下数学归纳法在中学数学中比较常见的应用,加深学生对数学归纳法的理解.
三、数学归纳法的应用
数学归纳法可以解决很多类型的问题.下面主要介绍数学归纳法在恒等式和不等式证明中的应用,以及在数列、几何问题、整除性问题中的应用.
(一)数学归纳法在恒等式证明中的应用
利用数学归纳法进行恒等式证明时,整个过程只需做到等式两侧的数值相等.
例 1证明:n+(n+1)+(n+2)+…+(3n-2)= (2n-1)2(n∈N∗).
证明当n= 1 时,左边 = 1 = (2×1-1)2= 右边,等式成立.
假设当n=k时,等式同样成立,即
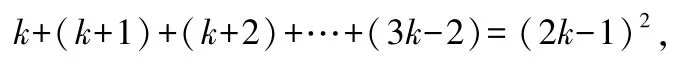
则当n=k+1 时,有

也就是说,当n=k+1 时等式成立,所以等式对于任意一个正整数n都满足.
(二)数学归纳法在不等式证明中的应用
应用数学归纳法解决不等式的证明问题时,可以对不等式两边的形式观察分析,特别是不等式左边的形式,然后再找出当n=k和n=k+1 时左式的差异,弄清这些是解决这类问题的关键.
例2证明
证明当n=1 时,不等式显然成立.
假设当n=k(k≥1,k∈N∗)时,不等式同样成立,即

则当n=k+1 时,


即n=k+1 时,不等式成立.
所以不等式对于任意一个正整数n都成立.
(三)数学归纳法在数列中的应用
有时应用数学归纳法解决数列的有关问题时,相对于其他方法思路可能要更通畅一些.
例 3设数列{an}的前n项和为Sn.已知求:(1)a2的值;(2)数列{an}的通项公式,并用数学归纳法加以证明;(3)求数列{an}的前n项和Sn.
解(1)将n=1 代入得a2=4.
下面用数学归纳法进行证明:
1)当n=1 时,a1=12=1,命题成立.
2)假设当n=k(k∈N∗)时命题成立,即ak=k2成立,则当n=k+1 时,有

即当n=k+1 时命题也成立.
综上可知,an=n2对于任何n∈N∗都成立.
(3)由(2)知an=n2(n∈N∗),则an+1=(n+1)2=n2+2n+1,

(四)数学归纳法在几何问题中的应用
数学归纳法不仅适用于平面的几何问题,也适用于部分立体几何问题.下面举例说明数学归纳法在几何问题中的应用.
例4设多个圆心在同一条直线且两两相交的半圆,试求:这些半圆的交点最多将半圆分割成多少个圆弧?
解设半圆个数为n,最多分割圆弧的个数为函数f(n),如图 1 所示,可知当n=2 时,f(n)=f(2)= 4=22.
当n=3 时,为了让三个半圆相交得到的圆弧最多,就应该让第三个半圆和前两个半圆都相交,如图2 所示,可得f(3)= 9=32.同理可知,当n= 4 时,f(4)= 16 = 42.因此猜想有n个半圆时,最多可以将半圆分割成f(n)=n2个圆弧.
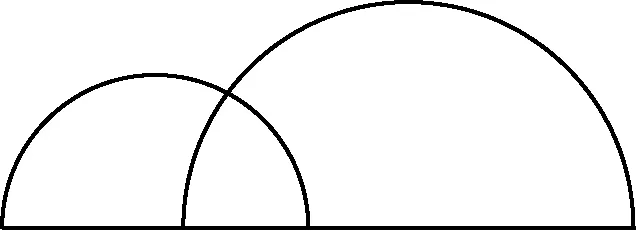
图1

图2
用数学归纳法进行证明:当n=2 时命题成立.假设当n=k时命题成立,即f(k)=k2.也就是说,当直线一边有k个两两相交的半圆时,最多可以分割成k2个圆弧.
当n=k+1 时,求第k+1 个半圆与之前的k个半圆都相交时可以得到最多的圆弧.
此时,原来前k的半圆都被第k+1 个半圆割出了一条新圆弧,有k条圆弧,第k+1 个半圆都被原来所有的半圆分割成了k+1 个圆弧,因此f(k+1)=k2+k+k+1 =(k+1)2,故当n=k+1 时命题成立.即当有n个半圆时,可以将半圆最多分成f(n)=n2个圆弧.
(五)数学归纳法在整除性问题中的应用
利用数学归纳法解决整除性问题,首先需要知道一些整除性方面的知识,即如果a能被c整除,那么a的倍数na也能被c整除;如果a,b都能被c整除,那么它们的和或差a±b也能被c整除.
例 5证明:f(n)= (3n+1)·7n-1(n∈N∗)能被 9 整除.
证明当n=1 时,f(1)= (3+1)·7-1 =27,27 显然能被9 整除,故命题成立.
假设当n=k时,原命题成立,即f(k)= (3k+1)·7k-1能被9 整除,则

故f(k+1)=f(k)+9·(2k+3)·7k能被 9 整除.
综上可知,对于一切n∈N∗原命题都恒成立.
结束语
数学归纳法是中学数学中比较重要的学习内容,是证明命题成立的重要方法之一,它的核心就是递推思想,它可以很好地弥补不完全归纳法的不足,在多个教学环节得到了广泛应用.
