1种鲁棒的模糊聚类方法

汤 欢,胡恩良

(云南师范大学 数学学院,云南 昆明 650500)

聚类分析按照“物以类聚”的思想将无标签数据聚成不同的簇,实质是发掘出数据间的联系.随着众多学者的研究,许多聚类算法被相继提出,FCM[1](fuzzy C-means clustering)就是最具代表的聚类算法.将C-means聚类[2]结合模糊集合理论,是C-means的完善,且被广泛应用.然而FCM聚类算法也有不足,例如：FCM缺乏鲁棒机制,对噪声点或野值点很敏感.其本质原因在于：FCM聚类模型中的度量距离是欧氏距离的平方,故由噪音点或野值点导致的偏差会按“平方”幅度被放大,从而使得FCM缺乏鲁棒性.为了增加鲁棒性,文中采用“不带平方”的距离来代替“平方”距离,以此来抑制由噪音点或野值点导致的偏差被放大.“不带平方”的距离导致了非光滑的FCM,不能用原有的EM(expectation maximization)算法进行求解,为此采用了MM(majorization minimization)优化方法.实验结果表明,与传统FCM算法相比,RFCM具有更好的聚类性能.

1 FCM及鲁棒性分析

1.1 FCM算法

FCM聚类是硬聚类C-means的1种改进和推广.通过引入模糊集合理论[3],将HCM算法中隶属度矩阵推广到模糊隶属度矩阵.FCM算法根据模糊隶属度矩阵U,计算每个样本点隶属于某个类的隶属度uij∈[0,1].从而进行聚类.该算法最早由Bezdek[1]提出,将数据集X分成c个模糊类.采用“类内加权平方和最小化”的准则确定目标函数,形式如下：

(1)

在(1)式中,V={v1,v2,…,vc}为聚类中心,U=[uij]n×cFCM隶属度矩阵.uij表示样本xi对类vj的隶属度,m表示模糊指数(m越大模糊程度越高).特别地,若在(1)式中定义隶属度uij：

(2)

则式(1)就退变成C-means的目标函数.

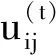
(3)

(4)

1.2 鲁棒性分析

FCM聚类模型中的度量距离是欧氏距离的平方,故由噪音点或野值点[7]导致的偏差会按“平方”幅度被放大,从而使得FCM缺乏鲁棒性.在模型(1)中,若xi是1个野值点,则它到聚类中心vj的偏差按平方“‖xi-vj2‖”增长得很大,从而统治了非野值点对应的项.虽然“距离平方”带来FCM的光滑性,方便了后续的求导运算,但这也将造成FCM对野值点很敏感,缺乏鲁棒性.

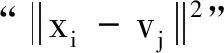
2 RFCM:1种鲁棒的FCM模型

2.1 模型建立

(5)

对比问题(5)和(1)的2个模型,很容易看出：

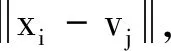
2.2 MM优化方法[5](majorization-minimization)

MM算法是1种迭代优化方法,它利用函数的凸性来找到原函数最小值.且EM算法是MM算法的1个特例.当目标函数较难优化时,MM算法找到易于优化的上界函数逼近于原目标函数.即每一次迭代找到1个原目标函数的上界函数,再求上界函数的最小值.

若满足：(i)g(θ|θ(t))≥f(θ) ∀θ; (ii)g(θ(t)|θ(t))=f(θ(t)),则g(θ|θ(t))就可作为f(θ)在θt处的代理函数或上界函数.在MM算法中,通过最小化g(θ|θ(t))而不是实际函数f(θ)来寻求下1个迭代点.MM算法是1种单调下降算法,即如果θ(t+1)为g(θ|θ(t))的最小值,则有：

f(θ(t+1))=g(θ(t+1)|θ(t))+f(θ(t+1))-g(θ(t+1)|θ(t))≤g(θ(t)|θ(t))+0=f(θ(t)).

2.3 RFCM模型的求解

定理1：(i)S(V,U|U(t))≥JRFCM(V,U)；(ii)S(V,U(t)|U(t))≥JRFCM(V,U(t)),其中

(6)

基于上界函数S(V,U),利用EM算法进行交替优化求解U和V.模糊聚类的隶属度矩阵U与聚类中心V更新公式都可求出封闭解.迭代序列如下：

U(0)→V(0)→U(1)→V(1)→…→U(t)→V(t)→…

该求解过程可整理成如下算法1.

算法1： RFCM求解

输入：数据集X,聚类别数c,聚类中心V(0),模糊指数m,最大迭代次数tmax,阈值ε,t=0.

输出：隶属度矩阵U*.

Step 1 更新模糊划分矩阵:

(7)

Step 2 更新聚类中心向量:

(8)

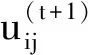
3 实验结果与分析

3.1 实验数据描述及信息

本文选取12个数据集(具体信息如表1)进行实验.它们分别是Blood,chessboard,CMC,Bupa, cancer, seed, Vechicle, WDBC, heart, iris, sonar和wine,均来自UCI数据集[6].

3.2 聚类纯度对比及分析

表2中,我们在12组数据集上对FCM和RFCM的聚类纯度[7]进行了对比.从表中可看出：除了在数据seed上RFCM聚类纯度比FCM稍微低点,在大部分数据上RFCM的聚类纯度都比FCM的聚类纯度高或者相等.而在数据集chessboard、iris上RFCM比FCM优势明显突出.

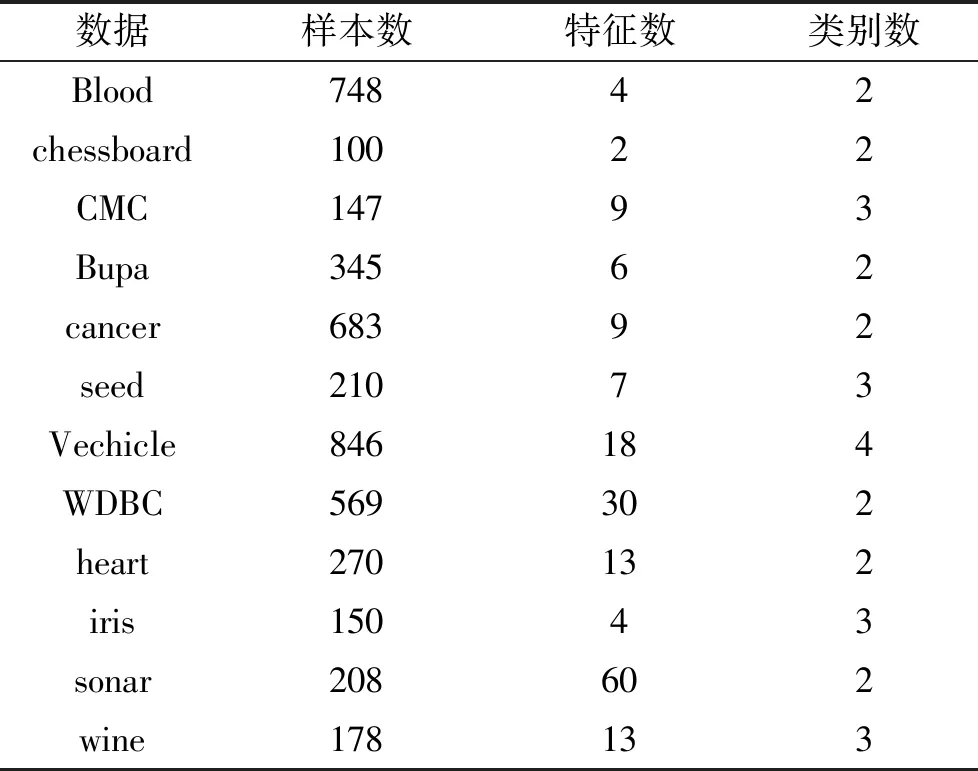
表1 RFCM数据集及相关信息

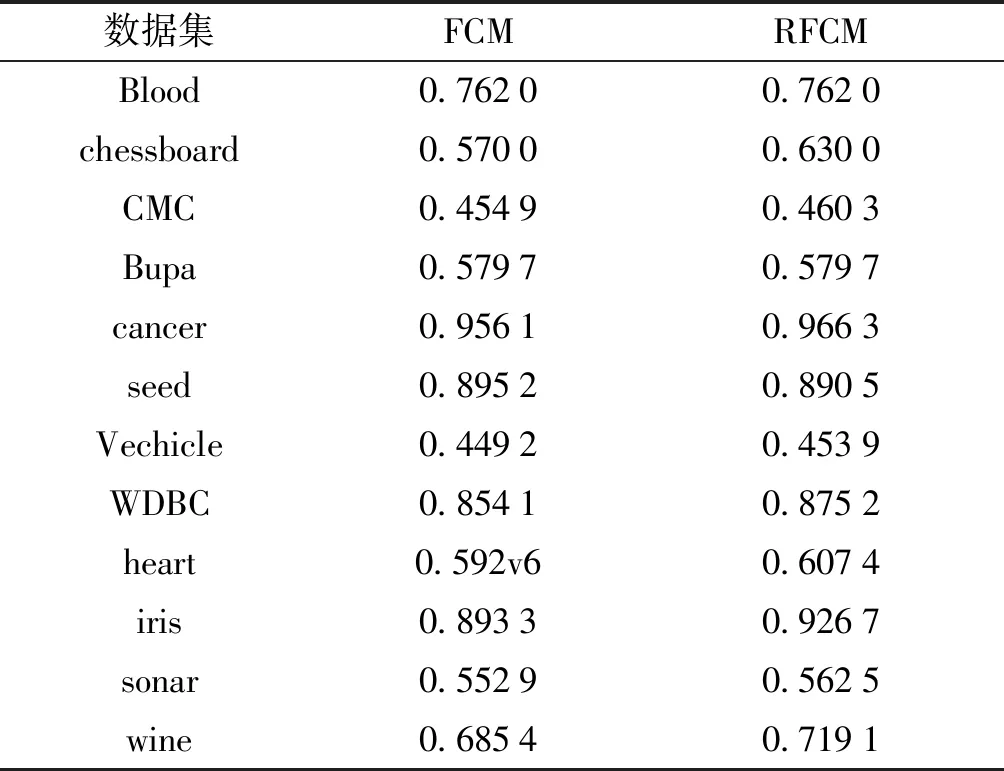
表2 RFCM与FCM在数据集上聚类纯度对比

表2中的结果分析：

2) 在seed数据集上,聚类纯度RFCM没有FCM方法高,其原因可能是该样本不同类(簇)上数据分布相对集中,或者受到模糊指数m的影响.

3.3 模糊指数m的选择

图3中,在4组数据集(wine、WDBC、chessboard、iris)上,通过选取不同的模糊指数m,对FCM和RFCM聚类纯度进行了对比.从表中可看出：FCM和RFCM聚类算法在m≥2时,聚类纯度都得到大幅度提高,且聚类纯度RFCM都要比FCM高,表现相对稳定.特别的,m=2,2.5时,RFCM总体效果较好.

4 结语

为了提高聚类效果,本文提出了1种鲁棒的FCM聚类算法RFCM.在RFCM中,我们将FCM的目标函数中度量样本到类(簇)中心的“平方”距离,替换成一般的“非平方”距离.其作用很大程度缩短了样本中噪音或野值点到类中心的距离,从而降低了野值点对类中心的影响,有更好的鲁棒性.通过实验结果可得出,RFCM方法比FCM具有更高的聚类纯度.未来工作中,可以进一步引入图论的知识来提高聚类性能.