给定度序列的三圈图的极值图
2020-09-11邵燕灵
杨 杨,邵燕灵
(中北大学 理学院,山西 太原 030051 )
化学图论主要研究化学分子图的拓扑不变量的性质与化合物的物理化学性质[1-5].分子拓扑指数就是反映化合物的结构特征的1种图的不变量,它用于描述化学结构,是将分子结构数值化的1种方式.
本文研究的所有图均为简单连通图[6-10].简单连通图G的度序列为π.文中图的的度序列均为非递增序列π=(d0,d1,…,dn-1).Tπ表示所有度序列为π的三圈图的集合.
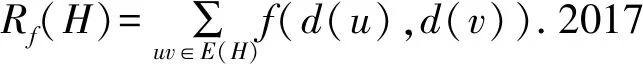
1 相关引理
定义1[10-11]设g(x,y)是N×N上的二元函数,如果对任意x≥y和a≥b,有g(y,a)+g(x,b)≤g(x,a)+g(y,b),当且仅当x=y,a=b时等号成立,则称g(x,y)是递增函数.相似地,如果对任意x≥y和a≥b,g(y,a)+g(x,b)≥g(x,a)+g(y,b),当且仅当x=y,a=b等号成立,则称g(x,y)为递减函数.
引理1[12]设g是递增函数,G∈gπ,pq,mn∈E(G)且pn,mq∉E(G).设M=G-pq-mn+pn+mq,如果d(p)≥d(m)且d(n)≥d(q),则Rg(G)≤Rg(M).
引理2[12]f是递增函数,若极值图G在gπ上使Rf最大化,G中的顶点记为{v1,v2,…,vn},其中v1为图G的根点,可满足以下条件:
(1)0≤h(v1)≤h(v2)≤…≤h(vn),h(v)表示顶点v到根点v1的距离;
(2)d(v1)≥d(v2)≥…≥d(vn);
(3)假设vpvq,vmvn∈E(G),vpvn,vqvm∉E(G),h(vq)=h(vn)=h(vp)+1=h(vm)+1,如果p 可图三圈图的度序列π可以分为以下几种情况. 1)d0≥d1≥4,且dn-1=1.这样的度序列构成的三圈图记为T1. 2)d0≥4>d1=d2=3,且dn-1=1.这样的度序列构成的三圈图记为T2. 3)d0≥5>d1=3,d2=2且dn-1=1.这样的度序列构成的三圈图记为T3. 4)d0≥6>d1=2,且dn-1=1.这样的度序列构成的三圈图记为T4. 定理1设n≥6,π=(d0,d1,d2,…,dn-1)是1个可图三圈图的度序列,d0≥d1≥4,且dn-1=1.则对任意递增函数f,存在1个极值图G在T1上使Rf最大化,使得v1v2,v1v3,v1v4,v1v5,v2v3,v2v4,v2v5∈E(G)且对所有x∈V(G){v1,v2,v3,v4,v5},有d(v1)≥d(v2)≥d(v3)≥d(v4)≥d(v5)≥d(x). 证明:根据引理2,存在1个极值图G在T1上使Rf最大化,并把G中的顶点标记为,v1为图G的根点. 1) 若vp-1,kvpi,vp-1,kvpj∈E(G)且i 2) 若vp-1,kvpi,vp-1,lvpj∈E(G)且k 有如下4个断言: 由以上4个断言可知,对任意递增函数,必存在1个极值图G,在T1上使Rf最大化,若记v1=v01,v2=v11,v3=v12,v4=v13,v5=v14,则v1v2,v1v3,v1v4,v2v3,v2v4,v2v5∈E(G),且对所有的x∈V(G){v1,v2,v3,v4,v5},有d(v1)≥d(v2)≥d(v3)≥d(v4)≥d(v5)≥d(x).定理证毕.d(v1)≥d(v2)≥d(v3)≥d(v4)≥d(v5)≥d(x). 定理2设n≥6,π=(d0,d1,d2,…,dn-1)是1个可图三圈图的度序列,d0≥4>d1=d2=3,且dn-1=1.则对任意递增函数f,存在1个极值图G在T2上使Rf最大化,使得v1v2,v1v3,v1v4,v1v5,v2v3,v2v5,v3v4∈E(G) ,且对所有x∈V(G){v1,v2,v3,v4,v5},有 d(v1)≥d(v2)≥d(v3)≥d(v4)≥d(v5)≥d(x). 家长是孩子的启蒙老师,是孩子的第一任教育者。温馨的家庭氛围和良好的家庭文化将对留守儿童产生巨大的影响。但是父母长期在外,导致家长角色弱化,父母与孩子产生隔阂,儿童应有的心灵归属缺失。 证明:类似于与定理1的证明,我们将有以下4个断言成立. 前3个断言与定理1的证明类似,以下证明断言4成立. 在极图H2上,因为d1=3,d2=3,有以下2种情况: 由以上4个断言可知,若n≥6,π=(d0,d1,d2,…,dn-1)是1个可图三圈图的度序列,d0≥4>d1=d2=3,且dn-1=1,对任意递增函数,必存在1个极值图G,在T2上使Rf最大化.若记v1=v01,v2=v11,v3=v12,v4=v13,v5=v14,则v1v2,v1v3,v1v4,v1v5,v2v3,v2v5,v3v4∈E(G),且对所有的x∈V(G){v1,v2,v3,v4,v5},有d(v1)≥d(v2)≥d(v3)≥d(v4)≥d(v5)≥d(x).定理证毕. 定理3设n≥7,π=(d0,d1,d2,…,dn-1)是1个可图三圈图的度序列,d0≥5>d1=3,d2=2且dn-1=1.则对任意递增函数f,存在1个极值图G在T3上使Rf最大化,使得v1v2,v1v3,v1v4,v1v5,v1v6,v2v3,v2v4,v5v6∈E(G) ,且对所有x∈V(G){v1,v2,v3,v4,v5,v6},有d(v1)≥d(v2)≥d(v3)≥d(v4)≥d(v5)≥d(v6)≥d(x). 证明:类似于与定理1的证明,我们将有以下4个断言成立. 前3个断言与定理1的证明类似,以下证明断言4成立. 由以上4个断言可知,若n≥7,π=(d0,d1,d2,…,dn-1)是1个可图三圈图的度序列,d0≥5>d1=3,d2=2且dn-1=1,则对任意递增函数,必存在1个极值图G在T3上使Rf最大化.若记v1=v01,v2=v11,v3=v12,v4=v13,v5=v14,v6=v15,则v1v2,v1v3,v1v4,v1v5,v1v6, v2v3,v2v4,v5v6∈E(G),且对所有的x∈V(G){v1,v2,v3,v4,v5,v6},有 d(v1)≥d(v2)≥d(v3)≥d(v4)≥d(v5)≥d(v6)≥d(x).定理证毕. 定理4设n≥8,π=(d0,d1,d2,…,dn-1)是1个可图三圈图的度序列,d0≥6>d1=2,且dn-1=1.则对任意递增函数f,存在1个极值图G在T4上使Rf最大化,使得v1v2,v1v3,v1v4,v1v5,v1v6,v1v7,v2v3,v4v5,v6v7∈E(G) ,且对所有x∈V(G){v1,v2,v3,v4,v5,v6,v7},有d(v1)≥d(v2)≥d(v3)≥d(v4)≥d(v5)≥d(v6)≥d(v7)≥d(x). 证明:类似于与定理1的证明,我们将有以下4个断言成立. 前3个断言与定理1的证明类似,以下证明断言4成立. 由以上4个断言可知,若n≥8,π=(d0,d1,d2,…,dn-1)是1个可图3圈图的度序列,d0≥6>d1=2,且dn-1=1,则对任意递增函数,必存在1个极值图G在T4上使Rf最大化.若记v1=v01,v2=v11,v3=v12,v4=v13,v5=v14,v6=v15,v7=v16,则v1v2,v1v3,v1v4,v1v5,v1v6,v1v7,v2v3,v4v5,v6v7∈E(G),且对所有的x∈V(G){v1,v2,v3,v4,v5,v6},有 d(v1)≥d(v2)≥d(v3)≥d(v4)≥d(v5)≥d(v6)≥d(v7)≥d(x).定理证毕. 给定度序列的k-圈图的极值图是图论研究工作者关注的焦点问题之一,具有一定的理论意义,它在物理化学中预测新型化合物的物理和化学性质.给定度序列的树、单圈图、双圈图的极值图均已经被研究,本文在此基础上研究了给定度序列的三圈图的极值图,将可图三圈图根据度序列分为4种类型,分别对这4种类型的三圈图给出其极值图,并拓展到具体的分子拓扑指数.2 主要结论
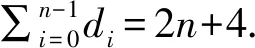
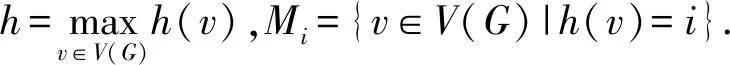
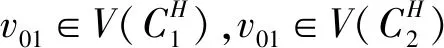
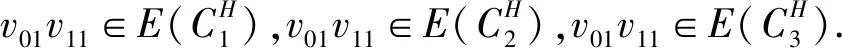
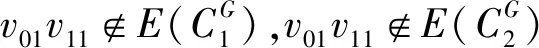
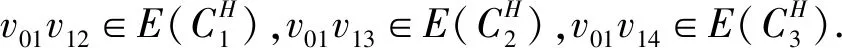
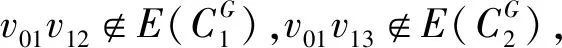
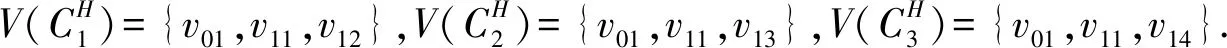
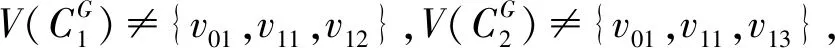
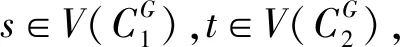
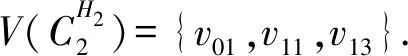
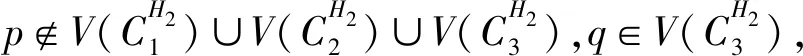
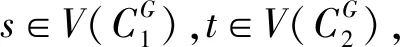
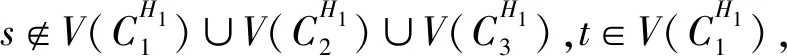
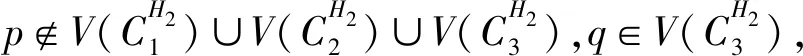
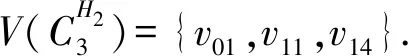
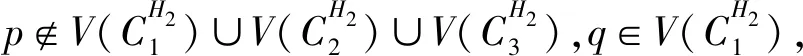
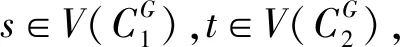
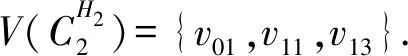
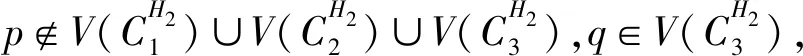
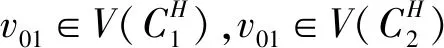
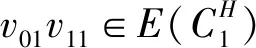
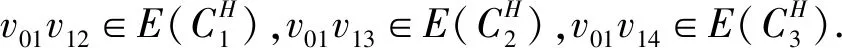
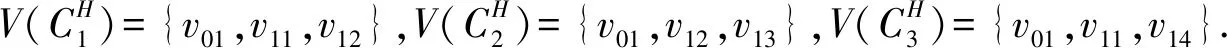
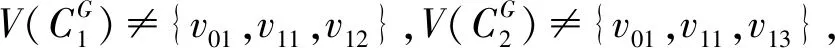
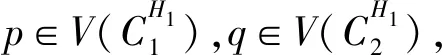
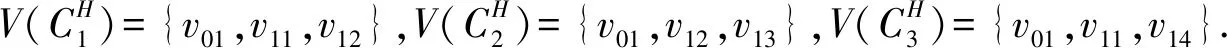
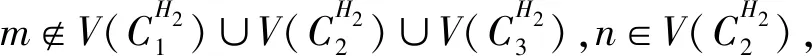
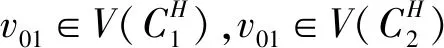
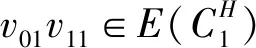
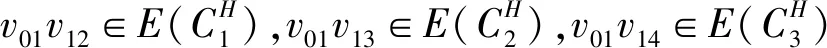
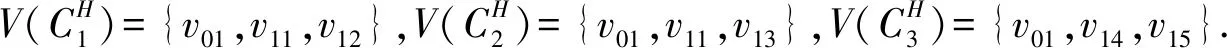
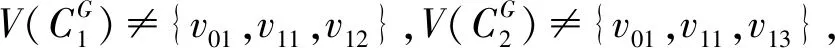
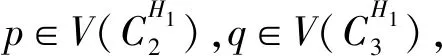
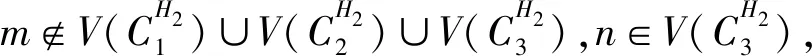
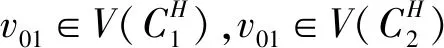
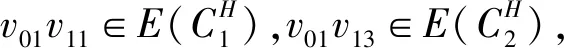
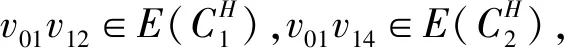
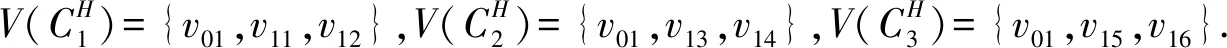
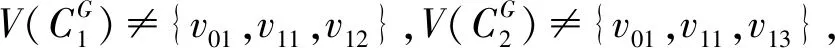
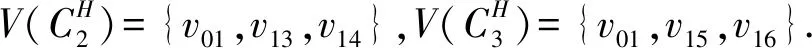
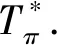
3 结语
