筒仓漏斗折板梁计算方法对比分析

霍云星

(泰戈特(北京)工程技术有限公司，北京 100022)

1 概 述

钢筋混凝土筒仓作为存储散料的特种结构，在选煤厂、电力、水泥、粮食等行业中大量应用，筒仓卸料漏斗常用的结构形式有角锥形、圆锥形等。角锥形漏斗常用的有2种形式，一种通过在梁下吊挂斜壁板，梁上填料，形成漏斗形结构；另一种通过2个方向的折板梁垂直相交形成1个漏斗的2个斜壁，此漏斗另外2个斜壁则通过与筒仓相连的内筒配合填料形成。在大直径筒仓中采用折板梁形成的漏斗，因折板斜壁可以形成卸料斜坡，与角锥形漏斗相比，折板梁处可节省大量填料。折板梁具有很大的抗弯刚度，通过折板梁处斜壁板和自身折板梁结构来抵抗上部物料的压力。在大直径筒仓卸料漏斗结构形式的选择中，折板梁漏斗从整体受力和经济造价方面有一定优势。

折板漏斗的折板梁下部纵向受力钢筋计算，以往手算通常采用简化的深梁计算，侧壁按3边支撑板进行配筋计算；对于折板深梁，因端部支座约束有限，介于刚接与半刚接之间，受力复杂，以往计算通过深梁计算下部和支座纵向配筋时，可通过端部铰接和刚接2种简化模型的计算来进行纵向配筋。因折板梁受力复杂，按深梁计算的配筋量也较小，一般通过最小配筋率和关键部位加大配筋构造来进行施工图设计。

目前在结构设计中，复杂结构节点的计算一般通过有限元应力分析来校核配筋。本文通过有限元软件MIDAS对折板梁建立实体单元模型，单元划分后，按照单元配筋方向拉应力大小，依据现行《水工混凝土结构设计规范》(DL/T 5057—2009)中有关非杆系钢筋混凝土结构配筋计算原则来计算配筋。通过实际折板梁配筋计算分析，明确了2种计算方法配筋的差别，为实际施工图配筋提供一定参考。

有限元分析可以弥补手算中局部应力集中等不易详细计算的部位，对以往通过概念设计构造配筋的关键部位可以用数据直观表示，对于折板深梁的配筋一般分为斜壁板配筋和下部纵向配筋，可以分别计算，按计算结果叠加出施工图(因篇幅有限，折板深梁侧壁配筋、裂缝验算等本文不做详细描述，同时对折板梁跨中下部受力钢筋计算作对比分析时不考虑地震作用和风荷载)。

2 折板梁布置及计算

2.1 折板漏斗布置

本文选取1个实际工程的φ21 m筒仓(储量1万t，贮料为精煤)的折板梁卸料漏斗为分析对象，该筒仓有4个卸料口，通过2个折板梁垂直相交形成每个漏斗中的2个斜壁，另外2个斜壁通过筒仓内筒填料形成，卸料口处漏斗平面和剖面布置如图1至图3所示。

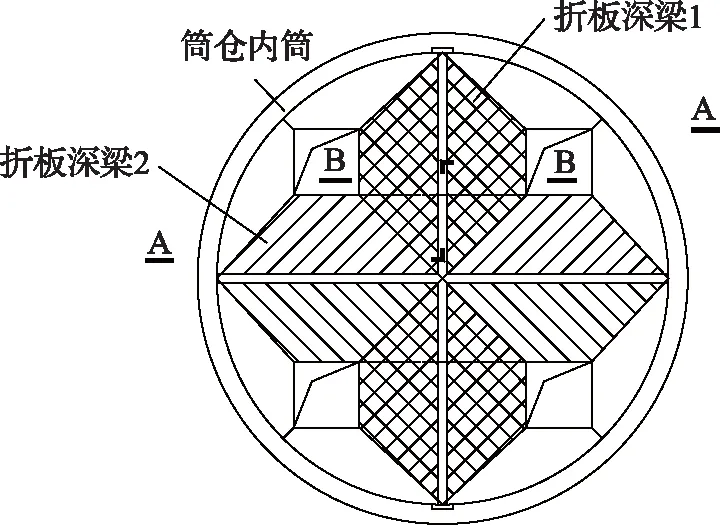
图1 漏斗平面布置

图2 漏斗剖面(一)

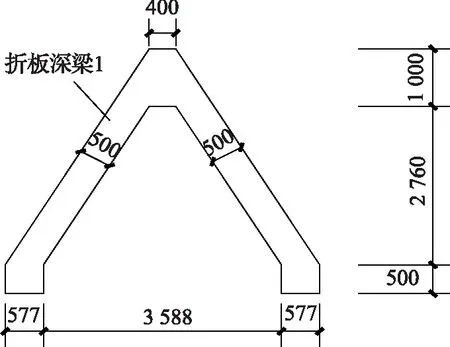
图3 漏斗剖面(二)

以下计算均按图3中漏斗剖面所注尺寸，梁纵向跨度按5 m考虑。

2.2 折板梁荷载

折板梁承受漏斗以上物料的压力，简化计算时折板梁上的荷载不考虑折板梁高度变化所引起的荷载变化，折板梁承受的物料压力依据《钢筋混凝土筒仓设计标准》(GB 50077—2017)可求得，计算模型的详细荷载如图4所示。

图4 折板梁实际荷载受力

折板梁计算仅考虑下部纵向计算配筋对比，为简化计算，以下分析中，按深梁模型计算时，荷载简化为线荷载，荷载简化图如图5所示；按有限元分析实体单元建模计算时，荷载简化为顶面承受的均布荷载，荷载简化如图6所示。

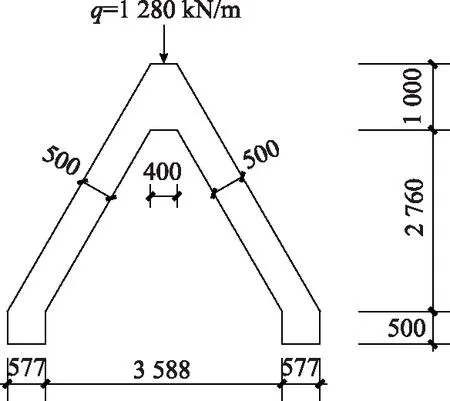
图5 折板梁按深梁计算荷载简化

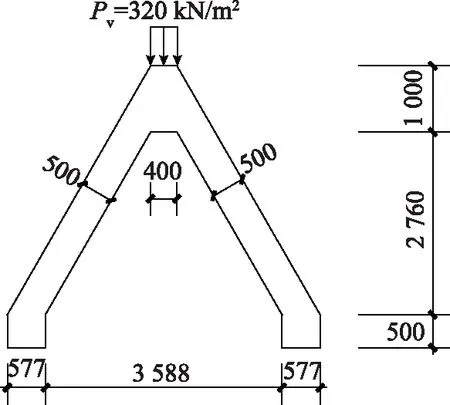
图6 折板梁按实体单元计算荷载简化

折板梁侧壁配筋时斜壁板按3边支撑板计算，也可通过有限原分析按板单元建模进行内力分析配筋，但侧壁配筋计算对与上述假定关于折板梁底部纵向钢筋的计算结果影响不大，所以以上假定不影响折板梁下部纵向钢筋的计算配筋(因篇幅所限对侧壁配筋不做介绍)。

以下模型分析计算时，物料荷载按活载取值，活载分项系数取1.4；自重按恒载取值，恒载分项系数取1.2。

计算分析时材料选用，混凝土强度等级取C30，纵向受拉钢筋取HRB400。

3 折板梁计算对比

3.1 折板梁按深梁简化计算分析

3.1.1 折板梁折换成矩形深梁简化模型

折板深梁计算时，常规设计方法为按照等高度和等惯性矩为原则，折换成普通矩形深梁，按矩形深梁进行配筋计算，惯性矩计算时可通过AUTOCAD中面域快速进行计算。折板梁按图3中尺寸计算的惯性矩为：I=6 606 280 776 729 mm4，折算成矩形深梁时计算公式为：I=(b×h3)/12，通过该公式可得折算矩形深梁的宽度为1 025 mm，转换后的普通矩形深梁计算模型如图7所示。

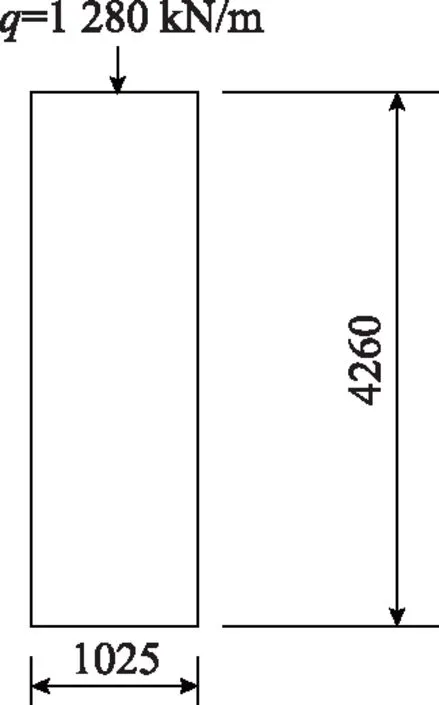
图7 折板梁转普通深梁计算模型

3.1.2 折板梁转普通矩形深梁配筋计算

对于筒仓下折板深梁配筋计算时的边界约束假定，因实际筒仓内筒对折板梁的约束并不能形成完全刚接，实际为半刚接。如按刚接计算所得的跨中弯矩比实际弯矩偏小，而完全按铰接假定，支座处配筋与实际不符。因此依据实际工程经验通过刚接和铰接分别计算，施工图中一般按铰接和刚接的计算结果取包络配筋，并结合最小配筋率和实际情况做配筋调整。

深梁配筋计算按照《混凝土结构设计规范》(GB 50010—2010)附录G进行。配筋计算公式如式(1)所示。

M≤fyAsz

(1)

z=αd(h0-0.5x)

(2)

式中：M——弯矩，N·mm2；

fy——钢筋强度设计值，N/mm2；

As——受拉区钢筋面积，mm2；

h0——截面有效高度，mm；

h——截面高度，mm；

l0——计算跨度，mm；

x——受压区高度，mm；

z——内力臂，mm。

按铰接计算时，单跨简支梁在均布荷载下计算的跨中弯矩为6 009 kN·m，依据此弯矩按照式(1)计算配筋，可以得出铰接时跨中下部纵向受力配筋面积为：As=4 306 mm2；

按刚接计算时，单跨刚接梁在均布荷载下的跨中弯矩为2 004 kN·m，依据此弯矩按照式(1)计算配筋，可以得出刚接时跨中下部纵向受力配筋面积为：As=1 435 mm2；

按转换后的深梁配筋时，依据混规附录G表G.0.12中规定，深梁纵向受拉钢筋的最小配筋率为0.2%，按最小配筋求得配筋面积为：As=8 733 mm2。

通过以上按铰接和刚接计算的配筋面积与最小配筋率计算的配筋面积比较取值，此处取下部纵向受力配筋总面积As=8 733 mm2。

3.2 折板梁按有限元实体单元建模计算

3.2.1 有限元建模简介

折板梁通过有限元实体单元模型分析时，采用MIDAS计算软件，净跨度按5 m建模，单元网格划分时取100 mm左右间距来分割单元，建模的荷载按图6所示输入。应力分析配筋计算时，采用纵向最大应力云图进行配筋。有限元模型分析时边界假定也采用2种方法，第一种按支座下部铰接进行分析，第二种按支座全部刚接进行分析。

3.2.2 有限元模型支座铰接假定分析

铰接计算简图如图8所示。

图8 支座铰接假定有限元模型

按图8假定，计算分析后的应力云图如图9所示。

图9 支座铰接假定纵向应力分布

通过图9可知下部跨中受力最大，此处取跨中断面处的云图查看单元应力，跨中断面云图如图10所示。

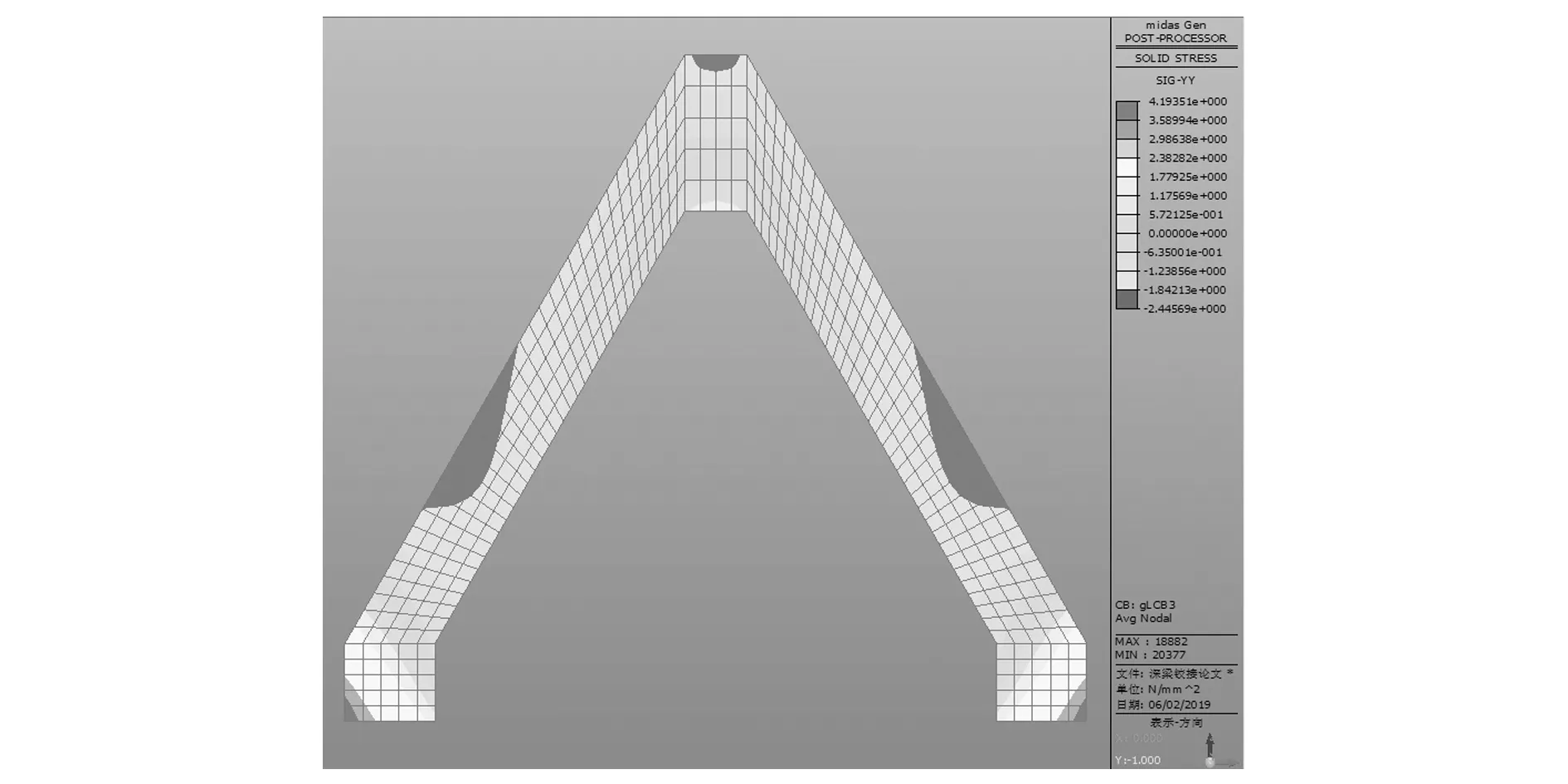
图10 支座铰接假定跨中断面纵向应力分布

从图10中看出下部单元拉应力最大，最大拉应力位置处数值如图11所示。

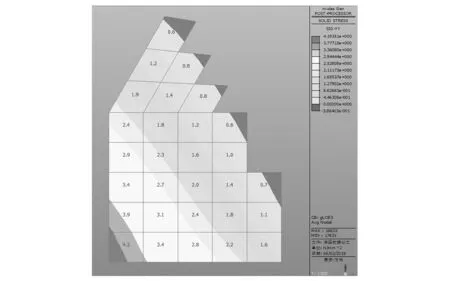
图11 支座铰接假定跨中断面纵向最大拉应力分布数值

3.2.3 有限元模型支座刚接假定分析

刚接计算简图如图12所示。

按图12假定，计算分析后的应力分布云图如图13所示。

本文仅研究折板梁下部纵筋的计算对比，通过图13可知下部跨中受力最大，此处取跨中断面处的云图查看单元应力，跨中断面云图如图14所示。

图14 支座刚接假定跨中断面纵向应力分布

图14中下部单元拉应力最大，最大拉应力位置处数值见图15。

图15 支座刚接假定跨中断面纵向最大拉应力分布数值

3.2.4 有限元分析结果配筋计算

通过以上2种支座假定计算结果的对比，可以看出不同假定下的折板梁底部最大拉应力分布区域，按刚接假定时依据图15，可知底部最大拉应力为σ1=1.8 N/mm2；按铰接假定时依据图11，可知底部最大拉应力为σ2=4.2 N/mm2。此处按受拉单元计算的总合力，铰接假定时大于刚接假定，对比分析时采用最不利假定，因此本文采用铰接假定的图11进行配筋计算。

有限元分析计算时，应力分析配筋一般用来校核常规计算的配筋量，本文应力分析配筋依据《水工混凝土结构设计规范》附录D中的有关规定，依据此条规定，截面正应力方向受拉钢筋的截面面积As按式(4)进行计算：

式中：T——由荷载设计值确定的主拉应力在配筋方向上形成的总拉力，N；

Tc——混凝土承担的拉力，N；

fy——钢筋强度设计值，N/mm2；

As——受拉区钢筋面积，mm2；

γd——重要性系数。

在常规设计中，配筋计算一般不考虑混凝土拉应力的影响。依据式(4)计算时，假定完全不考虑混凝土拉力Tc的影响，重要性系数对比分析时在此处统一取1，按此假定计算结果较为保守。

有限元分析配筋计算时，按照图11计算结果进行。图中单元面积与单元应力的乘积可求得折板梁底部总拉应力的合力，图11中拉应力单元面积按网格划分时网格间距计算，为计算方便，此处统一取为100×(577/5)=11 540 mm2，拉应力单元计算结果如表1所示。

由表1知，按铰接假定时折板梁跨中下部单元受拉部分总拉力T=660 088 N，依据式(4)可求得总配筋As=1 833 mm2。

4 计算结果对比分析

按矩形深梁和有限元分析模型计算的配筋结果如表2所示。

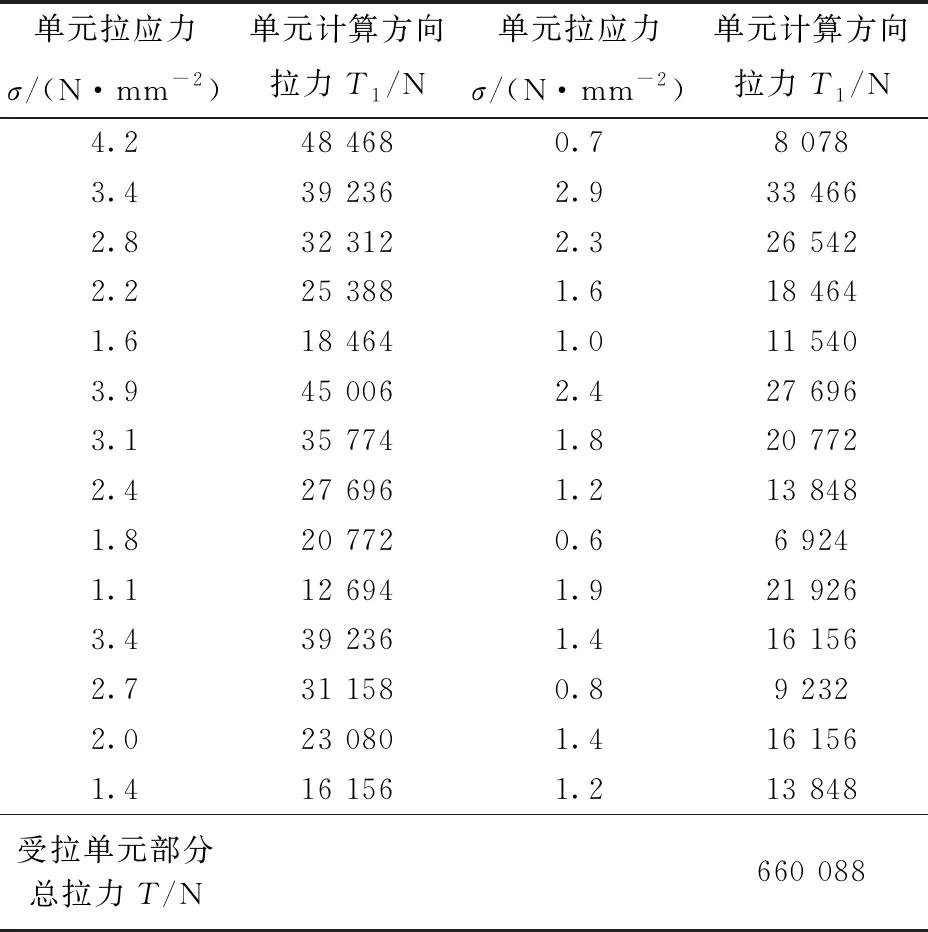
表1 折板梁跨中底部拉应力单元合力计算

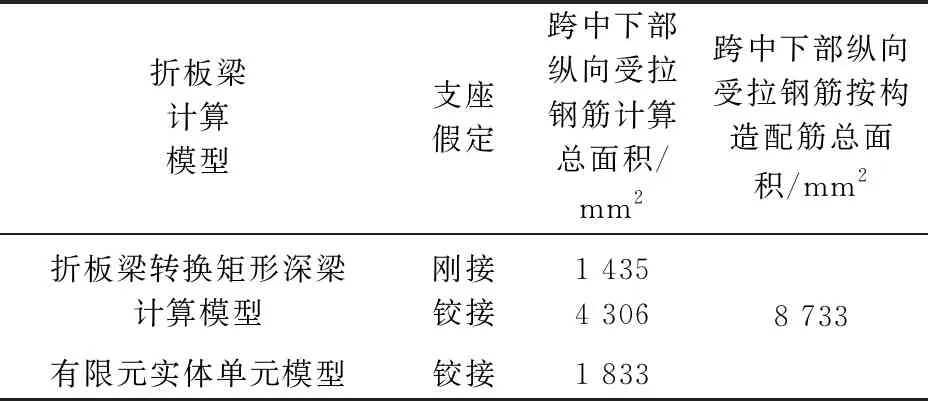
表2 不同计算模型下折板梁下部跨中配筋面积

由表2可知，有限元支座铰接假定计算的配筋面积介于按矩形普通深梁2种配筋方式计算的配筋面积之间，因考虑到深梁实际受力复杂，深梁变形较小，支座不存在完全铰接，以上计算结果与概念设计分析的结果是一致的，实际施工图中配筋一般按最小配筋率确定的总计算面积并结合裂缝计算进行跨中下部配筋，按构造配筋面积大于实际计算面积。

折板梁侧壁为3边支撑板，板厚由侧壁受力和构造确定，折板梁高度由工艺专业按卸料要求确定。实际折板梁结构计算时按工艺构造确定的高度进行，所以折板梁的高度和侧壁板的厚度在截面尺寸上优化难度较大，因此按此形式设计的折板梁抗弯承载力很大。直径21 m筒仓常规储量为1万t，折板梁跨中下部配筋由以上分析可知，按构造取值即可满足抗弯承载力的要求，承载力安全系数较高。

5 结 语

大直径筒仓卸料漏斗形式多种多样，采用角锥形漏斗时，如采用梁吊挂形式的漏斗，为满足工艺专业筒仓漏斗口布置和卸料坡度的要求，通过填料形成斜壁的填料用量较大，不能充分利用漏斗斜壁，性价比较低。

大直径筒仓常见的卸料口无论是4个还是6个，一般均可采用折板梁漏斗形式。通过折板梁的2个垂直相交的斜壁形成漏斗斜壁，折板梁本身作为承重梁承受仓内的贮料压力。

通过传统计算方法和有限元计算方法对比分析发现，在一定折板梁高度和厚度的前提下，折板梁的受弯承载力较大，仅按构造配筋即可满足上部物料压力的作用，安全系数较高。实际施工图中，漏斗口处因给煤机吊挂的要求，漏斗口封边梁配筋按预埋螺栓的构造要求设计后，也可作为折板梁下部纵向受力钢筋，可以额外提供一定的安全系数。

通过有限元分析，可以清晰地看到关键部位的应力集中，在应力集中部位通过加强构造配筋，来满足裂缝等要求。有限元分析作为现行复杂结构设计的一种计算方法，可以从细部微观上进一步量化关键部位的受力情况，为结构安全设计提供可靠保证通过对折板梁不同计算模型的对比分析还可以发现，对于折板梁这种将漏斗斜壁和跨间承重结构相结合的体系，结构合理、经济效果明显，是仓底漏斗承重结构的一种较好方案。