齿轮传动系统的动态性能分析和优化设计

李文善

摘要：为了分析多级齿轮传动系统的动态性能，构建了齿轮传动系统仿真模型，通过仿真，分析多级齿轮传动系统的主要物理参数对于齿轮传动系统动态性能的影响规律。并基于仿真得到的分析数据据和相应的实验测试数据，提出了应用谐波平衡法的多级齿轮传动系统优化设计方法，并获得最优设计参数。

Abstract： In order to analyze the dynamic performance of the multi-stage gear transmission system， a simulation model of the gear transmission system is constructed. Through the simulation， the influence law of the main physical parameters of the multi-stage gear transmission system on the dynamic performance of the gear transmission system is analyzed. And based on the analysis data obtained by simulation and the corresponding experimental test data， a multi-stage gear transmission system optimization method based on the harmonic balance method is proposed. The housing size parameters of the reducer and the basic parameters of the gear pair are used as design variables. The transmission ratio， actual center distance， gear tooth strength， etc. are constraints， and the root mean square value of vibration acceleration and the overall mass are the goals. A multi-objective hybrid discrete optimization model is established， and the program is solved based on the branch and bound algorithm to obtain the optimal design variable.

關键词：齿轮传动系统;动态性能;优化设计

Key words： gear transmission system;dynamic performance;optimization design

0  引言

多级齿轮传动系统相较于普通齿轮传动系统而言，具有体积小、质量轻、传动效率高、传动精度高、承载能力高等众多优势。精密设备的控制系统对于多级齿轮的传动性能在灵敏度界限、工作快速性和稳定性方面提出更高的要求。因此，有必要对多级齿轮传动系统的动态性能开展相关的研究。

1  建立多级齿轮传动系统的动态性能分析模型

1.1 构建多级齿轮传动系统的数学模型

依据刚度特性，多级齿轮传动与一般齿轮传动之间具有一定的差异，并且在负载与执行件之间安装径向啮合式多级齿轮传动的主要目的是为了传递动力、实现运动，所以必须要考虑到弹性与齿间侧隙的影响[1]。通过综合考虑弹性与齿间侧隙的影响，构建数学模型。

而模型中的IL为负载惯量，IM是执行电机转子和波发生器的惯量，制定电机的转角？渍M（t）进行折算，使其到输出轴上的转角以？渍M（t）=？渍M（t）/ih。

当系统存在齿间侧隙为2jt的情况下，可以采用以下的方程式来表示方程组。

从上述的公式中，充分考虑了元件弹性以及齿间侧隙的影响，其是一个非线性函数。在多级齿轮传动系统中，将电机到负载的系统当量为两个具有弹性元件的链接，为间隙隔开集中质量的运动传递，模型中的Ii为IM折算到输出轴上的惯量，？渍i（t）与Ti则为折算到输出端的输入转矩和转角。

1.2 建立多级齿轮传动系统动态性能仿真模型

在对于多级齿轮传动系统的动态性能建立数学模型后，利用SIMULINK组件能够实现多级齿轮传动系统的动态性能仿真模型的构建[2]。如图1所示为仿真模型。

1.3 仿真分析和结论

对于多级齿轮传动系统动态性能建立仿真模型，后进行仿真分析，从而确定传动系统中的主要物理参数，得出对于整个系统性能产生的影响规律。

利用某研究项目中应用的多级齿轮减速器为仿真对象，总传动比i=80、柔轮变形波数U=2，钢轮齿数z2=162，柔轮齿数z1=160，输入轴转速fH=9500r/min，啮合角？琢n=20°，额定负载60N·m，输入端转动惯量J1=0.00022kga·m2，输出端转动惯量J0=0.2839kg·m2，0是初始条件。通过进行各种试验之后，能够得出扭转刚度表达式各项，而齿间侧隙则是2？渍i=8′。

在设定仿真参数之后，将上述的各项参数开展仿真分析，以此来得到这些参数对于传动系统性能所产生的影响规律。

2  传动系统非线性振动特性的分析

对微分方程组进行求解，求解所用积分时间范围为300Tm。求解时，需要对二阶振动微分方程逐步进行降阶处理，方程可表示为：x2=f（t，x（1），x（2））。

2.1 转速对于系统非线性振动特性的影响

齿轮传动正逐步向高速和重载的方向发展，因此有必要对转速影响系统振动特性开展系统的研究，设定传动系统的无量纲频率在？赘=0.001～1.5在范围内变化。当？赘<0.2时，系统呈现出单周期的非谐响应特性。此时，系统位移反映的时间历程图即单周期曲线，并且频谱图分布在m？赘的离散点上。随着无量纲频率的增加，系统将会由倍周期分叉进入混沌运动。随频率的逐渐加大，系统响应状态呈无规律的反复变化，且运动的状态也更为复杂而多变，混沌区域出现了众多的周期性窗口，同时窗口宽窄呈现交替渐变趋势。随着频率的再次升高，齿轮副动载荷系数也将随之加大，系统将在无冲击状态下显现单边及双边冲击。当无量纲频率增至1附近时，动载荷系数出现最大值，冲击情况最为严重。

2.2 黏滞摩擦因数对于传动系统性能的影响

利用仿真分析可以得知在不同黏滞摩擦因数的响应曲线，如图2所示，而系统阶跃响应曲线如图3所示。

通过图2、图3，能够得到传动系统中黏滞摩擦因数对于传动系统的动态性能所造成的影响。随着黏滞摩擦因素的不断增加，而传动系统的相位差也在逐渐的扩大，出现这一问题的主要原因在于：随着黏滞摩擦因数的上升，传动系统中的摩擦力矩也会随之上升，这表示随着摩擦动态方程中阻尼项参数的不断上升，将会出现这些反应[3]。除此之外，还会导致多级齿轮传动系统中，机械效率逐渐出现下降情况。因此，在设计传动系统的过程中，必须要考虑传动系统的一定速递效率、一定快速性，在这一前提条件下，可以有效的降低系统的粘滞摩擦因数。

2.3 齿间侧隙对于多级齿轮传动系统的性能影响

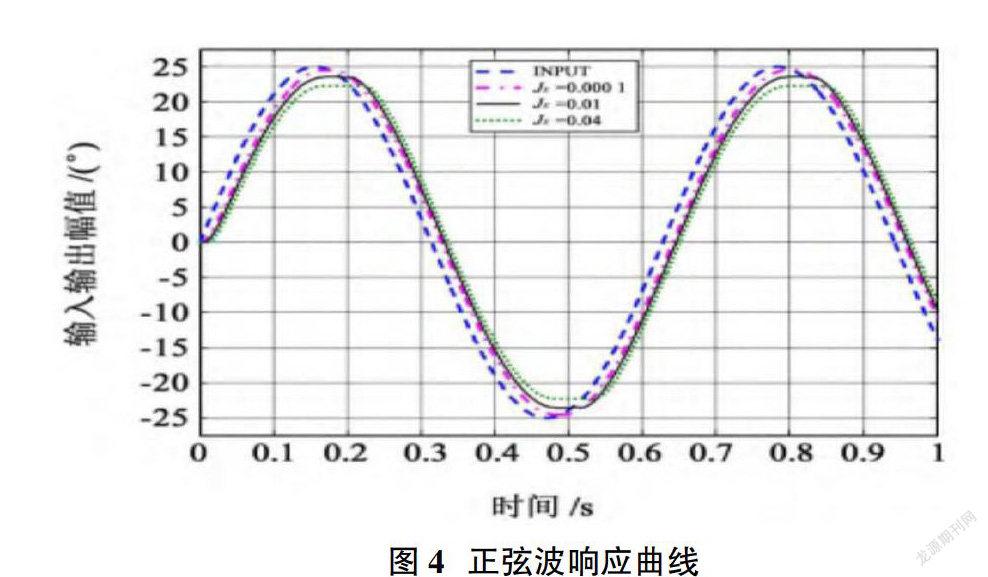
如果构建仿真模型采用齿间侧隙的话，其响应曲线如图4所示。而在采用不同齿间侧隙后，如图4所示为系统的阶跃响应曲线。

基于图4的曲线图，传动系统的传动间隙对于系统动态性能的影响主要体现在：当传动系统存在间隙时，响应的稳定性和快速性都会下降，同时因为存在间隙，所以虽然传动系统可以达到最佳的稳定状态，但是传动系统也同样会存在一定振幅的振动，并对于整个工作的稳定性造成严重的影响[4]。所以，在对于多级齿轮的传动系统进行设计和制造等过程中，需要以系统运动润滑为前提，同时满足这一前提条件下，尽可能的消除传动系统中所存在的装配间隙与其误差，以此来保障传动系统的设计功能。

3  多级传动系统的优化设计

3.1 优化设计变量

多级齿轮减速器具有结构复杂的特性，充分考虑减速器的安装环境及条件，设减速器外型尺寸不出现较大变化，随后逐一选取传动系统和对应壳体中的关键性几何参数作为设计的变量。传动系统的设计变量为齿轮的模数（m）、齿数（Z）和齿宽（b），对应壳体的变量分别为各子块的壁厚（β），累计设置15个变量，其变量矩阵表达式：

3.2 目标函数

综合考虑减速器的抗振性及轻量化设计等两个方面的具体要求， 同时密切注意到传动系统与壳体间的振动响应幅值处存在较大差别的实际，采用线性加权组合法，构建出目标函数：

3.3 约束条件

一般而言，多级齿轮的总传動均比较大，考虑到齿数优化后可能会引起减速器总传动比发生变化，所以需要对总传动比提前进行约束。此外，因多级齿轮传动系统中存在最小齿数与总传动比之间合理分配的实际情况，且各齿轮齿数应取整数，故对应的取值范围如下：

众所周知，齿轮的大齿宽对应高强度。但齿宽过大会导致齿轮载荷分布不均匀，因此有必要设置宽径比约束条件。实际生产中，为便于加工和测量，通常将齿宽的结尾数值取0和5。综上所述，齿轮宽径比约束取值范围如下：

3.4 优化模型求解

多级齿轮传动系统动态性能优化模型其实质为一个多目标混合离散规划，离散设计变量为齿轮的m，整型设计变量分别为z、b和β。本文利用Matlab软件和分枝定界法思想编程求解，其算法的基本过程简述如下：

首先，确定相互啮合的各级齿轮m的组合，其可行域设定为6。

其次，获得满足齿数、装配、传动比、邻接和中心距等约束条件的齿数组合可行阈值。

第三，在确定的齿轮m和齿数等约束条件下，逐步求解满足轮齿强度、宽径比约束条件的齿宽可行域6;随后，获取目标函数的局部最优解并存储相关信息。

最后，变换m及z再次进行计算，便可获得局部最优解集合，局部最优解集合中使目标函数最小的设计变量即为全局最优解[5]。通过上述混合离散优化求解，便可得到多级齿轮传动系统的设计变量最优值。忽略齿侧间隙和摩擦力矩等非线性因素会在一定程度上影响到优化计算的准确性，为检验优化效果，将优化后设计变量值，代入考虑非线性因素的减速器耦合系统集中参数模型中，计算构件的振动加速度和质量，将优化后各构件的振动加速度均方根值和质量除以优化前的相应值，可得到优化后振动加速度均方根值和质量的相对值[6]。

3.5 优化结果

优化后的具体结果如表1所示。优化后多级齿轮传动系统中的振动速度降低，传动系统构件振动加速度均方根值平均降低36.8m/s2，较优化前减小了33.5%，实现了减振的目的;传动系统质量降为2532kg，较优化前减小了12.96%。

4  结语

综上所述，通过分析齿间侧隙对多级齿轮传动系统的动态性能造成的影响，以此为基础构建传动系统的模型，通过仿真，分析传动系统中的齿间侧隙、黏滞摩擦因数等主要参数对系统动态性能的影响。最后，通过对某一型号的多级齿轮传动系统进行优化，得到了优化参数，并且传动系统重量减轻，性能也得到了提高。

参考文献：

[1]张强，李洪武.车辆多级行星传动系统扭振特性分析与优化[J].机械科学与技术，2019，38（3）：339-343.

[2]孙刚，任尊松，辛欣，等.高速动车组齿轮传动系统振动特性[J].机械工程学报，2019，55（18）：104-111.

[3]吴涛，周建星，张文祥，等.行星齿轮传动系统动态均载性能与灵敏度分析[J].机械设计与制造，2019（4）：171-175.

[4]郑凯峰，李伟，程立勇，等.模拟发动机驱动的变速器传动系统动态性能台架试验[J].汽车零部件，2019（6）：68-70.

[5]崔慧娟.齿轮传动系统动态特性与传动效率研究[J].内燃机与配件，2019（15）：73-74.

[6]符升平，项昌乐，姚寿文，等.基于刚柔耦合动力学的齿轮传动系统动态特性[J].吉林大学学报（工学版），2011，41（2）：382-386.