智能材料磁流变液垂直连续冲击减振器理论与实验
2020-09-10樊富起
樊富起


摘要:本文基于智能材料磁流变液冲击减振系统的阻尼效应与时域进行了理论推导,将数值仿真和物理模拟试验结合起来进行比对、研究冲击减振系统对流变液体钢性和柔性运动特性;系统固有频率总能抑制系统的振动得到揉性平衡谐振的结论。
关键词:磁流变液冲击减振器;垂直连续减振系
中图分类号:TB535.1 文献标识码:A 文章编号:1674-957X(2020)22-0073-02
0 引言
磁流变冲击减振器是利用磁流变液在自由冲击体活塞电场与磁流变液谐振系反复磁力线碰撞产生的能量损耗和动能量交换达到减振目的。由于其具有简单的结构、控制较易、体积也较小且对安装空间的要求也较低,目前不但用于飞机机翼的颤振抑制控制,而且也开始了在精密的数控机床等冲击减振器的应用。近年汽车研究人员想把这种技术用于汽车减震和车身钢度控制以及电动汽车的反充电上,该项技术正在研究之中。本文将解析分析、数值仿真和实验结合起来研究磁流变冲击减振器理论。
1 磁流变冲击减振系统响应情况分析
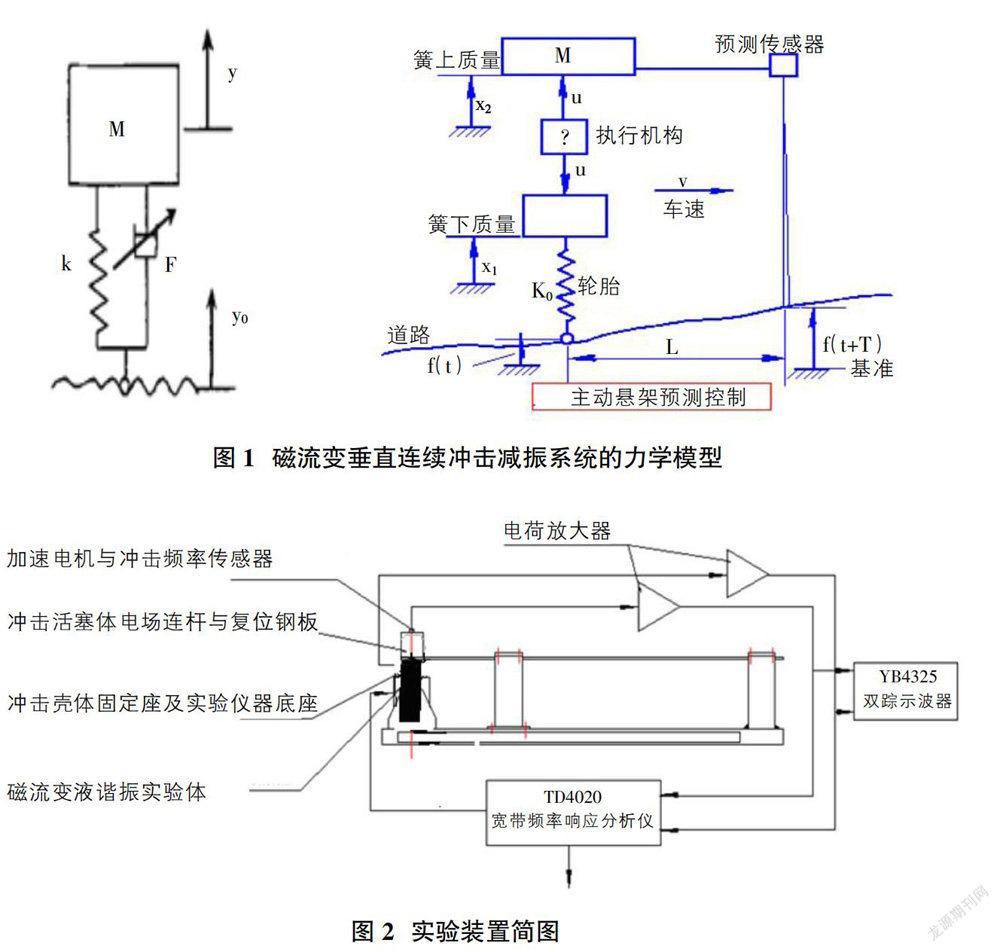
图1为力学模型。磁流变减振系由悬臂梁、减振器外壳组成。质量为m的冲击体活塞电场杆件放置于质量为M的容腔内,它们之间的纵向空隙为0.03mm。磁流变谐振系在外部简谐激振力Fsi(ωt)的作用在车架上将产生振动,当产生的激振力足够大,并且系统参数可以满足某种条件时,传感器将信号传给中央处理器、冲击体活塞电场将克服重力接通活塞磁场电源,磁流变液在容腔中作磁力运动,并和主质量发生碰撞。
建模时采用以下假设:
①磁流变自由冲击体活塞电场与减振器壳体的碰撞为瞬时弹性碰撞,满足动量守恒定律;②主系统是线性系统,适用叠加原理;③系统的运动过程中,磁流变本体处于冲击状态(冲击体活塞电场悬空)或粘附状态(冲击体活塞电场与磁流变谐振体作绞接运动)。
2 实验与仿真分析
实验装置如图2所示,悬臂梁为研究对象,悬臂梁的材质为弹簧钢板,悬臂梁的悬伸长度可调,悬臂梁的尺寸为1000×50×5mm,E=2.057×1011Pa,ρ=7718kg/m3,悬臂梁的悬伸量为195mm。在悬臂梁的左端固定冲击减振器,减振器壳体质量为0.4176kg,冲击体活塞电场的质量为0.266kg,磁流变液0.65kg壳体容积350mml,把激振器固于实验装置支架上,实验装置的激振点位于冲击减振器的正下方。有信号发生器置于TD4020型宽带频率响应分析仪内,将实验产生的信号送至功率放大器,通过调节使之始终保持为简谐信号。通过频率响应分析仪对系統进行动态特性测试,得到各频率对应的相频、幅频值。利用测得的幅频值来估算共振频率、阻尼比和留数,即估算模态参数。系统的动力学特性就可以通过这些模态参数完整地描述出来了。
通常,一个系统的若干阶模态振型的叠加可用来表示它的动态响应。若一定频带内只有一个重要的模态,就可单独确定该模态的参数。用电流变液质量的阻尼变量系数来表示悬臂钢板等效载荷,其二阶系统的速度幅频特性表达式为:
进行拟和,拟和曲线如图3所示。得到:A=2.44;fn=52.65;ξ=0.0041。
则给定激励力F,减振器安装处位移响应可由A0=H(f)·F(2?仔f)获得。
冲击减振位移测量:
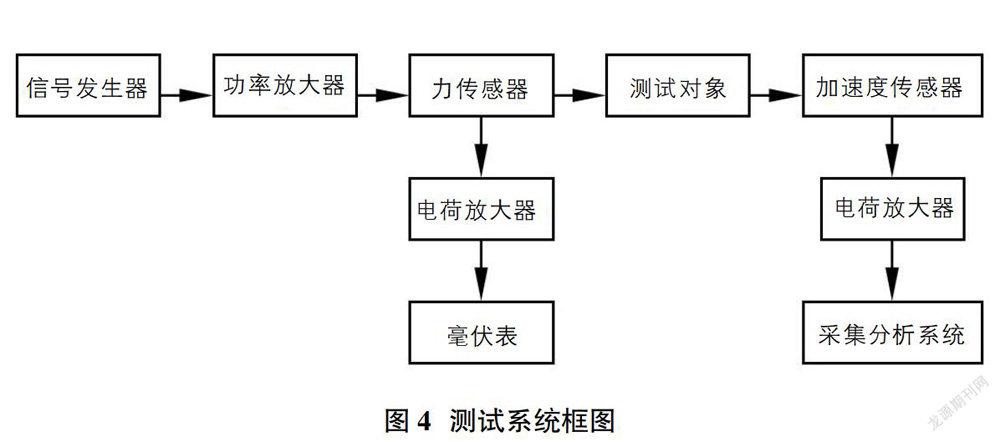
将冲击体活塞电场放入减振器壳体,调整冲击体活塞电场的冲程2h=1.5mm,测出减振器安装处的位移。测试系统框图见图4。
用毫伏表测出作用力的大小,而采集分析系统得出磁流变谐振系的位移响应。
恢复系数的测量:
恢复系数需有实验测定,在通常情况下,对于材料固定的物体,碰撞过程结束和开始的速度大小比值是不变的,该比值为恢复系数,用k表示,电场阻尼活塞自高处向减振器低处下降,并在弹片上连续弹跳,此弹跳过程中的信号用声卡采集到电脑,用任相邻两次碰撞的时间间隔算出碰撞恢复系数:。
用此法测出e=0.59。
冲击减振器的减振效果定义为:1-A/A0,其中A为磁流变谐振系装有减振器时的振幅,A0为磁流变谐振系统原来的振幅。
激振频率的影响:激振频率是影响减振效果的一个重要参数,取激振力F=6.17N,选用扫频间隔选为1Hz的稳态正弦手动扫描激振,来测试悬伸端的响应情况,绘出减振曲线,把该减振曲线与数值仿真计算获得的减振曲线进行比较。从图5可以观察到在该系统固有频率附近减振效果是最好,当实际产生的激振频率偏离系统的固有频率时,减振效果很快降低,表明冲击减振器对激振频率是比较敏感的。
激振力幅值的影响:选系统的共振频率作为激振频率,改变激振幅度,来测试悬伸端的响应情况,获得图6所示曲线,从图上看出减振曲线变化平缓,即冲击体活塞电场的运动状态对减振效果并无太大影响,这对工程应用具有指导意义。
3 结论
①本实验和仿真减振曲线趋势上基本上吻合,说明智能材料(磁流变液)减振系统的响应计算和数值仿真是正确的;②在电场接通后系统固有频率总能有效抑制系统的振幅和振频,且在落差大和差度小时减振效果最佳,因此更适应于自激振动系统,且总能保持最稳定的时域;③共振频率端、系统的减振效果对外激励的幅值大小很敏感。
参考文献:
[1]夏季,廖伯瑜.振动台上冲击减振器双面冲击运动的研究[J].力学与实践,2015,3.
[2]徐志伟,等.垂直冲击减振系统的仿真研究[J].西安交通大学学报,2017,5.
[3]丁文镜.减振理论[M].清华大学出版社,2015.
[4]任建庭.磁流变液夹层梁的动力学分析.西北工业大学汽车工程研究所,2016,12.
[5]S.F.Masri. T.k Caughey. On The Stability of The Impact Damper, Trans ASME, JAM, 2017.4.
[6]会强,郑堤.基于磁流变液的回转式阻尼器设计与有限元分析[J].宁波大学学报,2018,12.
