兰新高速铁路双弓-网系统动态耦合性能研究
2020-09-10常占宁张一平张玺王英
常占宁 张一平 张玺 王英












摘 要:为保证高速铁路弓网系统电能供应稳定性,基于弓网动力学理论对采用双弓受流方式的弓网系统动态受流特性进行了研究。以兰新高铁双弓网系统为背景,利用模态分析法建立了接触网和受电弓动力学模型,并在弓网动力学方程中添加前弓激励项进行了修正;通过分析高速动车组在不同车速和双弓间距下的弓网接触压力变化规律,从机械振动机理的角度对双弓-网间接触压力振荡特性进行了解释,得到了高速运行状态下的双弓-网系统动态受流特性。研究结果表明:随着列车运行速度的提高,前、后弓接触压力的振荡幅度均有不同程度的增加,后弓的受流质量受车速的影响更为显著;双弓运行时,不同双弓间距对前、后弓的影响程度不同,后弓受双弓间距的影响更为显著,选取合适的双弓间距可有效提高后弓受流稳定性。
关键词:兰新高速铁路;双弓-网系统;车速;双弓间距;接触压力;受流特性
中图分类号:U225.3 文献标识码:A
随着电气化铁路高速化、重载化、重联化方向发展,弓网系统动态耦合稳定受流日益重要[1]。为保证动车组电能供应连续,采用双弓受流方式是解决弓网供电不稳定的有效方法之一[2]。
目前,弓网系统动力学研究已引起国内外学者的广泛关注。文献[3-4]基于振动力学理论,考虑弓头弹簧的垂向运动,分别建立了计算精度较高的接触网和受电弓动力学模型。文献[5]建立了受电弓-接触网动态相互作用模型,从弓网垂向位移、接触压力变化等方面对弓网系统动态特性进行研究。文献[6]基于空气动力学理论,推导得到了作用于接触网线索上的环境风气动载荷,并仿真分析了环境风速、风攻角对弓网接触压力的影响。文献[7]通过非接触式红外热像检测进行了稳态双滑板接触点测温实验,验证了在不同弓网接触压力、双滑板不同距离情况下的稳态温度分布,并对弓网系统动态性能进行了分析。文献[8]针对刚性悬挂接触网,基于变刚度弹簧接触网模型,对弓网耦合动力学仿真方法进行了优化。文献[9]基于有限单元法,研究了高速列车通过隧道时产生的受电弓空气动力学效应对弓网动力学性能的影响。文献[10]对双弓作用下的弓网动力学行为进行了研究,探讨了双弓间距对弓网动力学性能的影响。文献[11]针对我国京津城际线参数,对高速弓网系统动态受流性能及动车双弓运行时双弓之间的最佳距离进行了仿真研究。目前,有关弓网动力学研究主要围绕单弓-网系统展开,针对双弓-网系统动力学的研究相对较少,且基于车速和双弓间距改变所引起的高速双弓-网系统动态受流特性的变化规律和形成机理有待进一步深入研究。
为此,本文针对西部兰新高速铁路双弓网系统为背景,首先对采用双弓受流方式的高速弓网系统进行动力学建模,基于模态分析法在以往弓网动力学方程中添加前弓激励项进行修正,得到双弓-网耦合动力学方程;随后,考虑动车组车速和双弓间距的影响,通过仿真求解分别研究不同车速和双弓间距对弓网受流的影响,从机械振动机理的角度来对不同工况下的双弓-网间接触压力振荡特性进行解释,得到合适的运行车速范围和双弓间距大小,以期为后续优化高速重联动车组弓网动态受流质量提供参考和依据。
1 双弓-网耦合系统数学建模
1.1 接触网建模
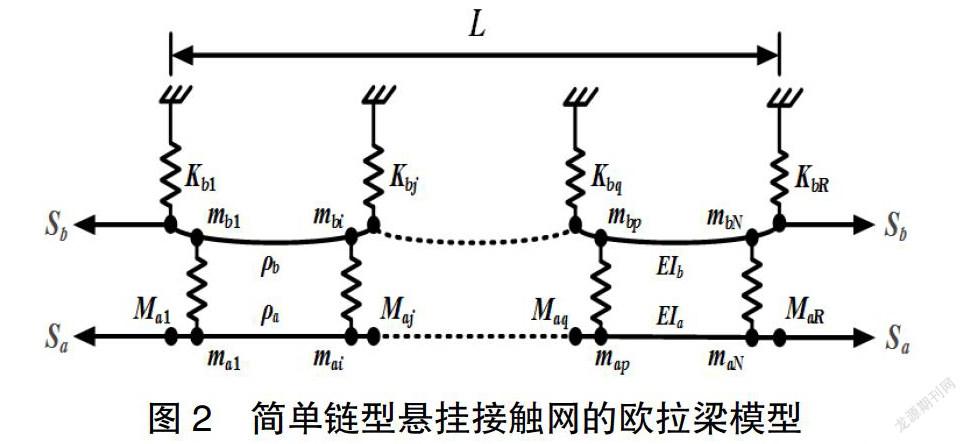
考虑到线索本身具有一定刚度,可将承力索或接触线等效为一根具有抗弯刚度、线密度且两端加有恒定张力的欧拉梁模型[12],取其微分段dx进行受力分析,如图1所示。接触网线索等效欧拉梁模型见图2。
图1中,S为该微分段两端张力;θ为张力与水平面夹角;M为截面弯矩;τ为截面剪切应力;C为系统自阻尼;F(x,t)为该微分段单位长度所受外力大小。
图2中,ρ为接触网线索线密度;m为吊弦集中质量;M为定位器质量;K为支撑杆弹性系数;EI为抗弯刚度;L为锚段长度。
通过对接触线或承力索的微分段进行受力分析,利用牛顿第二定律以及弯矩平衡定理推导可得该简单链型悬挂接触网的振动微分方程式为:
根据偏微分方程理论,式(1)的解可设为:
将式(2)代入式(1)中,可得接触网线索的动力学微分方程为:
式(3)中,为模态函数,为接触网线索的自振角频率,为主振函数。令An、Bn分别为承力索和接触线各阶对应的模态函数,N、R分别为吊弦和支撑杆及定位器的个数,Fc2、Fc1分别为前、后弓网间的接触压力,xr为后弓与接触线间的接触点位置,D为双弓间距。基于模态分析法,可得承力索与接触线的第n阶动力学微分方程式分别为:
式中:FA1(x,t)和FA2(x,t)分别为吊弦和支撑杆施加于承力索的作用力,FB1(x,t)和FB2(x,t)分别为吊弦和定位器施加于接触线的作用力;和分别为承力索和接触线的自振角频率。它们分别表示为:
其中,MD和KD分别为定位器的质量和刚度;MA和KA分别为支撑杆的质量和刚度;MB为定位器质量。
1.2 受电弓建模
对于受电弓模型,本文采用三质量块模型来对左、右受电弓进行数学建模,如图3所示。
图3中,y1、y2、y3,y4、y5、y6分别为前、后受电弓弓头、上框架及下框架的归算抬升位移;M1、M2、M3分别为前、后受电弓弓头、上框架及下框架的归算质量;K1、K2、K3分别为前、后受电弓弓头与上框架之间、上下框架之间、下框架与底座之间的归算弹簧刚度;C1、C2、C3分别为前、后受电弓弓头、上框架及下框架的归算阻尼系数;F0,P0分别为作用在前、后受电弓下框架的升弓力。因此,前、后弓运动微分方程分别为:
其中,接触压力Fc2和Fc1可采用罚函数法定义:
式中,Ks為弓头与接触线耦合时的等效弹簧刚度。
1.3 双弓网系统动力学建模
联立式(4)、(5)和(10)、(11)即可得到双弓网耦合动力学方程组,由于该微分方程组变量较多且难以直接求解,因此用矩阵形式来表示该微分方程组:
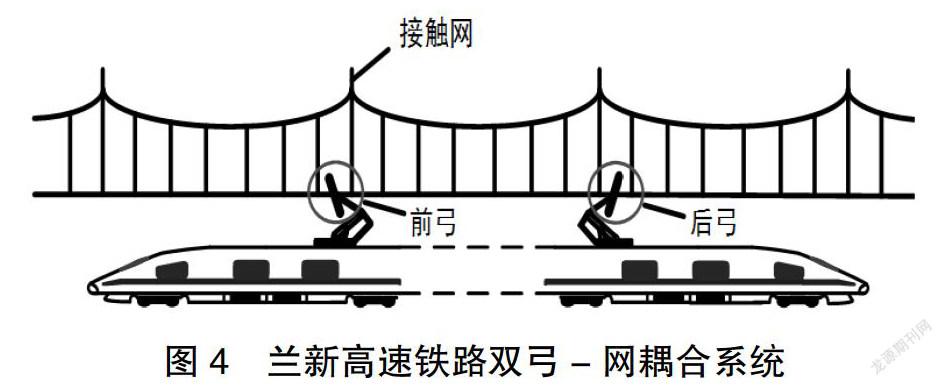
式(14)中:M为该双弓网耦合系统的质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为外界激励。图4表示双弓网耦合系统示意图。
1.4 模型验证
根据EN 50318标准建模参数[13],对250 km/h和300 km/h速度下的弓网模型进行动力学仿真,取3-8跨弓网接触压力统计数据与EN 50318标准进行对比。由表1可见,各项参数均符合标准范围。
2 不同车速下的双-弓网动态受流性能分析
标准TB/T3271[14]中规定,当交流系统时速大于200 km时,接触力范围为0 N~350 N。接触力标准差的最大值不应超过0.3倍的平均接触力目标值。接触力标准差越小表明接触力的集中程度越高,弓网接触质量越好。
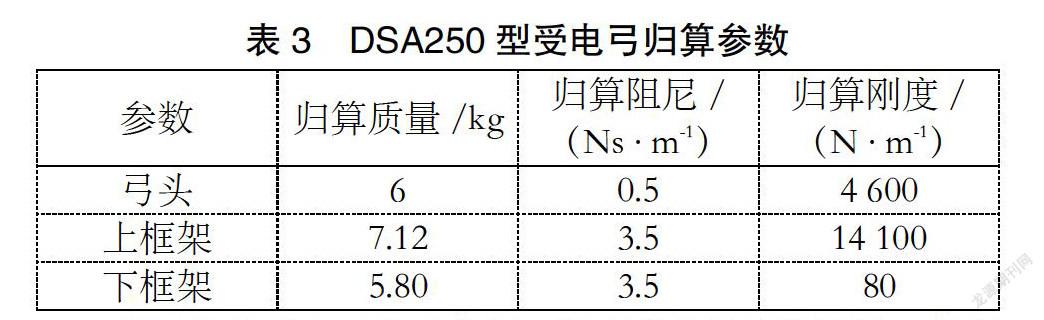
以西部兰新高速铁路为研究对象,该线路接触网参数见表2;受电弓选取DSA250型参数,如表3所示。设定动车组双弓间距为200 m,兰新线运行车速范围为200 km/h~
250 km/h,速度间隔为25 km/h,前、后弓的仿真跨数均取12跨,为保证仿真数据的有效性取3-8跨区段弓网接触压力数据进行分析,如图5所示。表4为兰新高铁不同车速条件下双弓-网间接触压力统计数据。
通过接触网在受电弓作用下所表现出的刚性性能,从机械振动机理的角度来对双弓-网间接触压力的振荡特性进行分析。由图5可以看出,双弓运行状态下的高速动车组后弓接触压力的振荡幅度比前弓更加剧烈,且后弓接触压力幅值较前弓明显更大,因此在不同车速下,后弓始终受前弓滑动接触所引起的振动波的干扰较大,而前弓则相对较小。
由表4可以看出,前弓和后弓接触压力平均值均随着车速的提高而增大。当车速为200 km/h时,前弓接触压力标准差为最小值,此时由后弓在接触线上滑动所引起的振动波对前弓接触受流的影响较小,弓网间受流较为稳定;当车速为250 km/h时,此时后弓引起的振动波干扰强度较大,接触压力出现大幅振荡,弓网间受流质量不佳。
由后弓接触压力数据可知,当车速为200 km/h时,后弓接触压力标准差最小,此时由前弓在接触线上滑动所引起的振动波对后弓受流的干扰较小,弓网间受流质量较好;但当车速高于225 km/h时,后弓接触压力出现振荡,此时弓网间受流情况下降。
通过对双弓数据进行对比,后弓接触压力标准差在各车速下均比前弓更大,且随着车速提高,后弓接触压力波動较前弓增幅更加明显。由此可知,在列车高速运行过程中,由前弓滑动接触引起的振动波对后弓受流干扰比后弓对前弓受流干扰更强,前弓受流更稳定,后弓受流质量受运行速度影响更显著。
3 不同双弓间距下的双弓网动态受流特性分析
随着重联动车组在我国兰新等高速铁路中的投入使用,选取合适的双弓间距成为影响弓网间受流质量的关键因素之一。本节设定动车组运行车速为200 km/h,双弓间距范围为100 m~250 m,间距间隔为25 m,其对应的双弓-网间接触压力曲线,如图6所示。
表5为不同双弓间距条件下的双弓-网间接触压力统计数据。由图6和表5可以看出,当双弓间距不同时,前弓接触压力无明显变化,其标准差的变化范围在5 N以内,且均符合TB/T3271标准,而后弓接触压力变化较为显著,其标准差变化范围在29.21~41.33之间。当双弓间距取100 m和150 m时,后弓在运行过程中出现弓网离线现象。当双弓间距为225 m时,后弓接触压力标准差为最小值,此时由前弓滑动接触引起的振动波对后弓受流的影响相对较小,弓网受流较为稳定;当双弓间距为100 m时,后弓接触压力标准差达到41.33 N,此时振动波对后弓受流的干扰强度较大,对弓网受流不利。由此可见,双弓间距是影响后弓受流稳定性的关键因素之一,在一定的间距范围内,双弓间距并非越大越好。
4 结论
本文基于模态分析法,建立双弓-网耦合系统模型,在弓网动力学方程中添加前弓激励项进行了修正,得到了考虑双弓激励方式的弓网动力学微分方程组,进而对兰线高铁重联动车组双弓-网系统动态受流特性进行了分析。主要结论如下:
(1)随着列车运行速度的提高,前、后弓接触压力的振荡幅度均有不同程度的增加,后弓的受流质量受车速的影响更为显著。当运行速度高于325 km/h时,后弓在多个位置出现离线现象,不符合安全标准。
(2)双弓运行状态下的高速动车组后弓始终受前弓滑动接触所引起的振动波干扰较大,而前弓受后弓的影响相对较小。当双弓间距不同时,后弓接触压力变化显著,选取合适双弓间距可有效提高后弓受流的稳定性。
参考文献:
[1]吴积钦.受电弓与接触网系统[M].西南交通大学出版社,2010.
[2]LU Xiaobing,LIU Zhigang,ZHANG Jing,et al.Prior Infor mation-Based Finite-Frequency H Control for Active Double Pantograph in High-Speed Railway[J].Transactions on vehicular technology,2017,66(10): 8723-8733.
[3]李丰良,粟谦,孙焰.接触网的力学模型及运动微分方程[J].长沙铁道学院学报,1996,18(02):90-93+112.
[4]李敏,李丰良,马俊.高速受电弓的力学模型及运动微分方程[J].铁道科学与工程学报,2005,27(03):83-87.
[5]梅桂明,张卫华.受电弓-接触网系统动力学模型及特性[J].交通运输工程学报,2002,2(01):20-25.
[6]宋洋,刘志刚,鲁小兵,等.计及接触网空气动力的高速弓网动态受流特性研究[J].铁道学报,2016,38(03):48-58.
[7]王英,刘志刚,母秀清,等.受电弓双滑板下的弓网电接触稳态热流分析与验证[J].铁道学报,2015,37(05):27-33.
[8]吕青松,王世轩,周宁,等.基于变刚度弹簧模型的弓网动力学分析[J].电气化铁道,2014,25(05):25-29.
[9]李瑞平,周宁,张卫华,等.高速列车过隧道对弓网动力学影响分析[J].振动与冲击,2013,32(06):33-37.
[10]周宁,张卫华.双弓作用下弓网动力学性能[J].西南交通大学学报,2009,44(04):552-557.
[11]吴燕,吴俊勇,郑积浩,等.高速受电弓-接触网动态受流性能及双弓距离的研究[J].铁道学报,2010,32(04):
38-43.
[12]CHEN Xiao-qiang,ZHANG Xi,WANG Ying,et al.I mprovedstudy on the fluctuation velocity of high-speed railway catenary considering the influence of accessory parts[J].IEEE Access,2020(08):138710-138718.
[13]European Standard EN 50318.Railway application-current collection syste ms-validation of si mulation of the dyna mic interaction between pantograph and overhead contact line.2002,European Co m mittee for Electrotechnical Standardization.
[14]中华人民共和国铁道部.TB/T 3271-2011 轨道交通 受流系统 受电弓与接触网相互作用准则[S].北京:中国铁道出版社,2011.
