基于双向流固耦合的铁路客车水箱冲击分析

戴忠晨　闫海宁　刘建军　付宁宁

摘要：以铁路普通客车水箱为研究对象，针对列车在加减速过程中对水箱内液体冲击晃动的问题，通过采用双向流固耦合方法进行仿真分析。得到了箱内气液两相流分布状态，获得水箱应力时间历程图和水箱位移历程图，实现对水箱结构强度更为准确的研究分析。通过与无防波板时水箱进行比较，进一步明确了防波板在受到冲击时所起的缓冲作用，为铁路客车水箱结构的设计提供了实用可靠的分析方法。

关键词：水箱;双向流固耦合;数值分析;结构强度

中图分类号：TG457文献标志码：A文章编号：1001-2303（2020）04-0079-06

DOI：10.7512/j.issn.1001-2303.2020.04.13

0 前言

铁路客车水箱是列车必备设备之一，用以保证列车上乘客和乘务人员的饮用以及生活用水。随着铁路列车的大幅提速，在列车加减速时水箱所受到的冲击晃动作用明显增强。因此，利用双向流固耦合方法对水箱内的液体进行晃动冲击仿真，找出水箱结构的薄弱环节对保证列车安全稳定的运行具有重要意义。由于水箱结构相对复杂，目前国内外对铁路客车水箱结构的相关研究较少[1]，大多以结构形式相对简单的储液容器为研究对象。如陈志伟[2]以移动式压力容器为研究对象，利用FLUENT软件对带自由液面的液体晃动进行仿真分析，研究了液体晃动对壁面的冲击作用以及容器内的防波板装置的分布情况。苟兴宇等[3]基于航天耦合动力学，对不同类型模型的耦合理论进行了深入研究。刘奎等[4]以罐车为研究对象，利用FLUENT软件，通过VOF模型对制动时的液体晃动过程进行了仿真分析，并与实验结果进行对比，研究防波板在整个晃动过程中的作用。刘小民等[5]研究了铁路罐车刹车过程中的液体晃动，发现罐体端面受力随充液比的增加而增大。徐刚等[6]通过对罐车进行仿真分析，得出了罐箱减速的初始阶段流固耦合对罐箱的运动影响最大。上述研究主要针对储液容器在结构安全性方面的设计，其研究方法是将流体域的计算结果通过插值的方法加载到固体结构的边界上，都是利用单向流固耦合方法。此类方法既不能获得储液容器随时间而变化的应力分布情况，也不能反映通过固体结构变形对流体域的影响。本文基于欧拉描述法多相流模型，利用双向流固耦合方法，根据《GB/T 21563-2008轨道交通机车车辆设备冲击和振动试验》的相关标准，获得了液体冲击晃动过程中箱体应力的时间历程图和水箱结构的位移历程图。

1 计算模型及计算方法

1.1 水箱结构

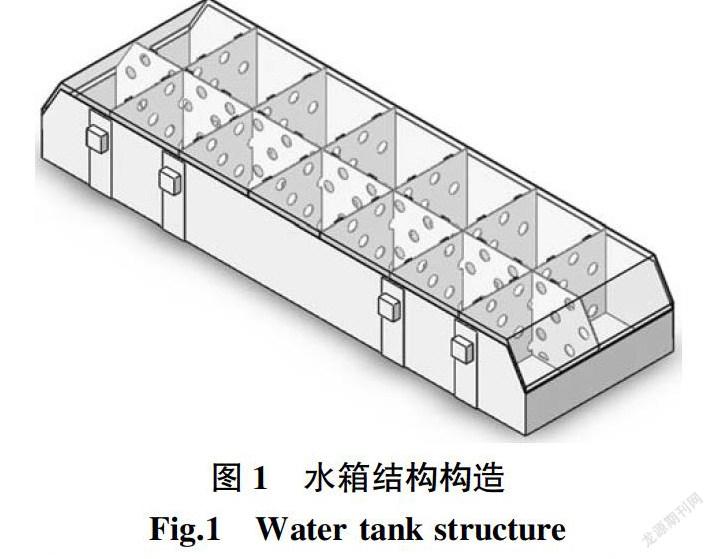
铁路客车上的方水箱为不规则长方体，尺寸为2 650 mm×810 mm×410 mm，重282 kg，容水量800 L，如圖1所示。方水箱由水箱顶面、水箱底面、纵向防波板、横向防波板、扎带、吊座组成等零部件焊接而成。为方便计算，在建模过程中省略了注水口、溢水口、供水孔、通气孔及检查盖等零部件以及焊接时应力集中的情况。

水箱材料主要为06Cr19Ni10不锈钢，它在空气中或化学腐蚀介质中能够形成一种氧化膜以抵抗腐蚀的高合金钢，其材料属性如表1所示，水箱安装位置如图2所示。

1.2 计算模型

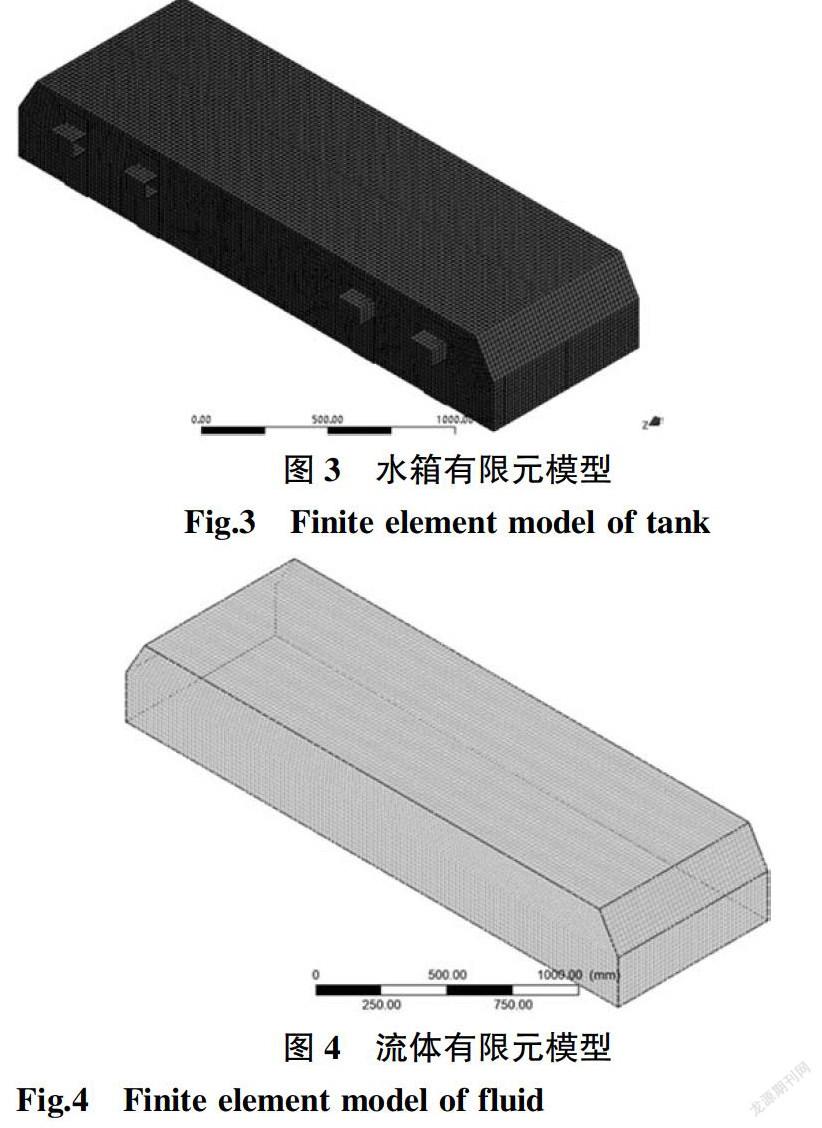
以铁路普通客车水箱模型为研究对象，通过SCDM软件建立薄壁箱体结构的力学模型。在CFX模块中设置流体域，在Transient structure模块中设置水箱结构。因为水箱为薄板结构，所以在SCDM建模过程中通过抽取中面将水箱建成板壳单元模型。通过Meshing功能分别对结构域和流体域进行网格划分，由于耦合参数通过插值传递，同时SCDM建模是一体的，在划分网格时保证了耦合边界上网格和各种参数的传递性，水箱结构有限元模型单元数为136 404，节点数279 539，有限元模型如图3所示。流体域有限元模型单元数为260 791，节点数420 743，有限元模型如图4所示。

1.3 控制方程组

水箱内部为气液两相流非稳态流动。本文采用VOF（Volume of Fluid）模型处理气液两相流且无传热现象对冲击晃动现象进行仿真，并采用k-ε模型模拟冲击现象。

VOF模型是建立在固定的欧拉网格下的表面跟踪办法，在两种或者多种流体（相）不相互混合的前提下，通过相体积分数实现对每个计算单元相界面的追踪。在流体域的每个控制容积体内，所有相体积分数总和为1，定义水为主相流，体积分数为α，则空气体积分数为1-α。

VOF模型满足的控制方程如下：

1.4 双向流固耦合

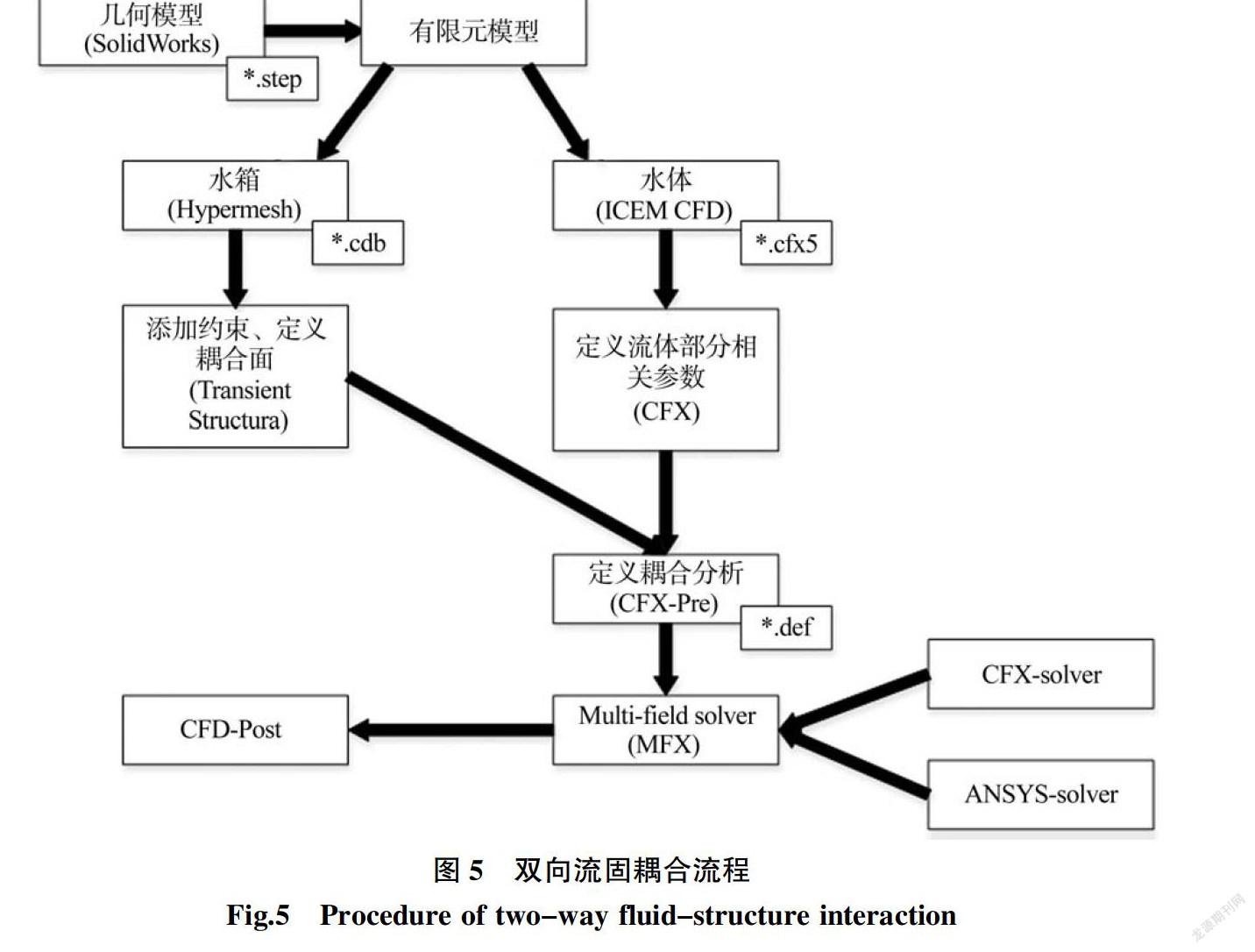
双向流固耦合分析的一般流程如图5所示。该方法的基本思路为：形成两套网格和边界，其中包含特殊定义的耦合边界和状态、参数，耦合软件将通过定义的耦合边界来传递耦合参数，并指挥流体、固体求解器计算，流体域和结构域分别由CFX模块和Transient structure模块进行瞬态计算。先在CFX模块中将流场压力作为直接解出量计算出流场压力分布，然后将其中的压力参数作为输出载荷加载到固体结构中，同时在Transient structure模块中将位移（变形）作为直接解出量计算出固体结构的位移（变形），将其中的位移参数作为输出载荷加载到流场中。由于双向流固耦合在每一步中都会进行数据交换，最后在求解设置中对最大、最小迭代步数进行设置，并将输出结果设置为瞬态结果，经过多步的数据交换以及数据迭代，最终达到一个平衡状态，各种参数最终收敛，得到能够反映结构域在流场边界条件下的各种瞬态结果，经过数据处理后绘制出结构应力、位移变化的时间历程图。

1.5 边界条件

双向流固耦合仿真分析分为流体域和结构域两部分，不能直接导入流体计算结果，而是预先设置一个流固耦合面，在计算过程中传递流固分析数据。本文选择固体结构的所有内壁面为流固耦合面，将流体的整个外表面设置为流固耦合面（FSI）。流体域边界条件为：对纵向方向施加用函数表达式编辑的峰值50 m/s2正弦半波冲击函数（见图6）和垂向重力加速度，设置盛水量（50%）、浮力参数、连续性表面及初始条件。不考虑传热影响，设置水箱内壁为不可滑移边界。固体域边界条件为：对水箱安装座施加固定约束。

2 结果分析

2.1 瞬态分析

首先通过双向流固耦合方法对水箱结构进行瞬态分析。模拟条件可任意选择，取盛水量为50%，冲击加速度为50 m/s2，增量步长0.02 s。不同时刻的水箱内气液两相分布情况如图7所示。

在水箱50%盛水量时对其施加纵向冲击载荷，其应力区域主要出现在水箱上箱盖处，最大值发生在0.76 s处，为26.58 MPa，小于水箱的屈服强度，此时位移变形为0.459 mm，等效应力云图和位移云图如图8、图9所示。其最大应力时间历程如图10所示。

2.2 无防波板比较

为了研究防波板在水箱中的重要作用，针对无防波板情况下的水箱进行了双向流固耦合分析。

如前所述，仍然在水箱50%盛水量时对其施加纵向冲击载荷，不同时刻下水箱内气液两相分布情况如图11所示。

其高应力区域出现在水箱上箱盖处，最大值发生在0.92 s处，为72.96 MPa，见图12。此时位移变形为12.280 mm，见图13。虽然无防波板时最大应力也小于水箱的屈服强度，但可以明显看出失去防波板的缓冲作用，水箱的冲击应力迅速上升，位移变形增大了30倍，由此可见防波板在缓和流体冲击时所起的重要作用。其最大应力时间历程见图15。

3 结论

本文以铁路普通客车水箱为研究对象，针对列车在加减速时水箱内液体冲击晃动问题，对整个过程进行了双向流固耦合数值模拟。得到了水箱盛水量为50%时，箱内气液两相流的应力时间历程图以及箱体位移时间历程图，并与无防波板情况下的水箱仿真分析结果进行了对比，得到结论如下：

（1）提出了一种针对铁路普通客车水箱的结构强度的分析方法和流程，并得到了水箱在冲击载荷作用下应力随时间的分布情况及应力时间历程图和位移时间历程图。

（2）通过与无防波板时水箱进行比较，发现失去防波板的缓冲作用后，水箱的冲击应力迅速上升，位移变形增大了30倍，可见防波板在缓和流体冲击时所起的重要作用。

参考文献：

[1] 吴作伟，梁闯，郭海霞. 基于双向流固耦合的动车组水箱强度分析[J]. 北京交通大学学报，2012，36（6）：42-46.

[2] 陈志伟. 移动式压力容器介质晃动数值模拟及防波装置研究[D]. 浙江：浙江大学，2006.

[3] 苟兴宇，王本利，马兴瑞，等. 航天工程中的贮箱類液固耦合动力学建模及耦合机理研究[J]. 强度与环境，1998，45（1）：9-16.

[4] 刘奎，康宁. 罐车制动时液体晃动的仿真分析[J]. 北京航空航天大学学报，2009，35（7）：799-803.

[5] 刘小民，许运宾. 部分充液罐车动力学特性的数值模拟与分析[J]. 西安交通大学学报，2011，45（6）：116-123.

[6] 徐刚，任文敏，张维，等. 储液容器的三维流固耦合动力特性分析[J]. 力学学报，2004，36（3）：328-335.

[7] 梁闯. 基于流固耦合分析的动车组水箱结构优化设计[D].北京：北京交通大学，2012.

[8] 胡萍. 基于双向流固耦合的200升水箱结构优化[D]. 北京：北京交通大学，2014.

[9] 李鹏飞，徐敏义，王飞飞. 精通CFD工程仿真与案例实战[M]. 北京：人民邮电出版社，2011.

[10] 胡潇毅. 一类流固耦合问题的数值算法及风场中摇曳树木的物理仿真[D]. 浙江：浙江大学，2008.

[11] Jeong K H，Lee S C. Hydroelastic vibration of a liquidfilled circular cylindrical shell[J]. Computers & Structures，1998，66（2-3）：173-185.

[12] Tsukimori K，Liu W K，Uras R A. Formulation of dynamic stability of fluid-filled shells[J]. Nuclear Engineering and Design，1993，142（2-3）：267-297.

[13] 李铁成，王熙林，李俊锋，等. 刚-流-弹耦合系统动力方程及其动力边界条件的建立[J]. 应用力学学报，1998，15（2）：127-131.

[14] Ibrahim R A，Barr A D S. Autoparametric resonance in a structure containing a liquid，Part I：Two mode interaction[J]. J. Sound Vib.，1975，42（2）：159-179.

[15] Pilipchuk V N，Ibrahim R A. The Dynamics of A Nonlinear System Simulating Liquid Sloshing Impact in Moving Structures[J]. Journal of Sound and Vibration，1997，205（5）：593-615.

[16] 岳宝增，王照林，匡金炉. 非线性晃动问题的ALE边界元分析方法[J]. 宇航学报，1998，19（1）：1-7.

[17] 卞荫贵. 粘性流体力学的数值解法[J]. 力学进展，1983，13（1）：19-33.