高考中函数题型的分析与解答探析
2020-09-10魏正余
魏正余


摘 要:函数是高中数学的核心考点,在高考中占有重要地位。为使学生能够灵活运用所学准确、高效地解答函数试题,在高考中取得理想成绩,应做好高考试卷研究,掌握函数常考题型以及考查的知识点,把握函数知识的命题规律与趋势,并做好函数试题的解答分析,授课中有针对性的讲解函数知识以及相关的解题方法,使学生切实打牢函数基础,提升函数试题的解题能力。
关键词:高中数学;高考;函数题型;分析;解答
高中数学涉及二次函数、指数函数、对数函数、三角函数等八大函数模型。同时,还包括函数的单调性、奇偶性、周期性等性质。相关题型复杂多变,难度中上以上,不仅需要学生牢固记忆不同函数的性质,而且还需理解相关结论的数学表达,能够从给出的数学表达式中分析、推导出函数的相关性质,以及时找到解题的突破口。授课中为提高学生的函数解题能力,高效解答相关高考试题,应做好高考题型的分析,并结合具体例题解答,使学生掌握解答函数试题的方法与技巧。
一、高考中的函数题型
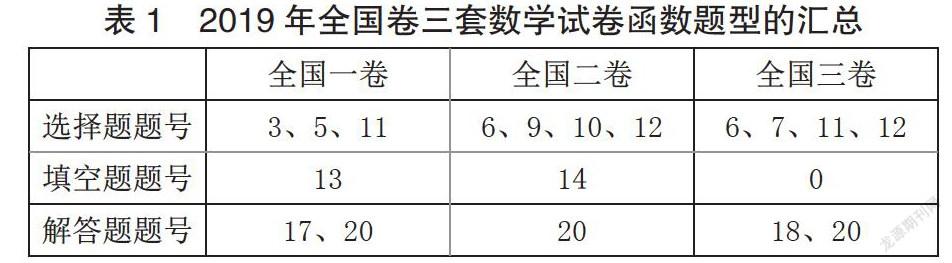
教学中做好高考中函数题型的分析,对学生进行针对性的训练,能够降低学生在高考中的陌生感,提升解答函数试题的自信。现对2019年全国卷三套数学试卷中有关函数的题型进行汇总(如表1所示)。
从表1中不难看出,高考中的函数试题,在选择题、填空题以及解答题中都有出现。其中选择题中的函数试题在3~4个,填空题占1个左右,解答题中占1~2个。其在三套试卷中对应题型中所占的分值分别为:25%、33.3%、33.3%。在填空题中所占的分值分别为:25%、25%、0%。在解答题中所占的分值为40%、20%、40%。由此可见函数在高考占者非常重要的地位。
鉴于函数在不同题型中都有出现,因此,在日常的教学中应做好函数各个题型的训练。同时根据不同题型既要注重解题技巧的传授,又要鼓励学生做好学习经验的总结。其中针对选择题可为学生讲解排除法、数形结合法、特殊值代入法等,使学生能够经过简单分析或运算选出正确答案。针对高考中的填空题可采取的解题方法有数形结合法、特殊值代入法、常规法。根据学生的作答情况来看,解答函数填空题使用常规法的比例较高,因此授课中应结合具体例题,为学生讲解常规的解题思路,使学生能够通法通解。针对函数解答题,一般考查的知识点有三角函数和导数知识。其中三角函数常和解三角形知识结合起来,为提高学生的解题正确率,应为学生细致的讲解正弦、余弦定理以及其和三角形外接圆之间的关系。同时在解题中引导学生注意一些细节,如探讨某个角度的三种函数取值时应注意在角度的取值范围,合理取舍。针对和导数知识结合起来的函数试题,一般难度较大,授课中要求学生准确记忆常规函数、复合函数的求导规律。
二、高考中函数试题的解答
授课中为使学生掌握高考相关函数试题的解答方法,应结合高考中的函数试题,为学生认真的剖析,讲解解题过程,给其以后解答类似的函数试题带来良好的启发。
1.选择题题型的解答
例1,已知a=log20.2,b=20.2,c=0.20.3,则()
A.a
该题目直接考查了对数函数与指数函数的相关性质,难度并不大。解题的关键在于能够联想出对应的对数与函数图像。对于对数函数当底大于1时,在x∈(0,+∞)单调递增。a=log20.220=1,0c>a,正确选项为B。
另外,高考中有关指数与对数函数的试题有时也和函数的单调性与奇偶性结合起来,难度有所增加,解题时需要运用函数的奇偶性,将其划到同一定义域内,而后运用函数的单调性进行求解,如以下题目:
例2,已知f(x)是定义域为R的偶函数,且在(0,+∞)上单调递减,则下列结论正确的是()
A.f(log3)>f()>f()
B.f(log3)>f()>f()
C.f()>f()>f(log3)
D.f()>f()>f(log3)
该题目不仅考查了指数和对数知识,而且考查了函数的奇偶性和单调性,较例1的难度有所增加。显然四个选项均涉及log3、、三个数,先对其进行分析。log31,因此,由f(x)在(0,+∞)上单调递减可知f()>f()>f(log3),正确选项为C。
2.填空题题型的解答
例3,曲线y=3(x2+x)ex,在点(0,0)处的切线方程为:____。
该题目较为简单,考查学生对导数几何意义的理解。在曲线上某一点处的导数,是指在该点处切线的斜率。根据所学可知,y'=3(x2+3x+1)ex,令x=0,可得y'=3。可知曲线的切线是一条斜率为3,过点(0,0)的直线。根据点斜式直线方程的求解方法可得y=3x。另外,填空题也有对函数奇偶性的考查。如以下题目:
例4,已知f(x)为奇函数,且当x<0时,f(x)=-eax,若f(ln2)=8,则a=___。
分析可知,利用给出的“f(ln2)=8”带入函数的表达式,可直接求解出a的值。但题目中给出了x<0时的函数表达式,而ln2>0未落在已知的x<0内,因此不能直接代入,需要应用“f(x)为奇函数”这一条件进行轉化。因为ln2>0,则-ln2<0。又因为f(ln2)=-f(-ln2)=e-aln2=8,即,2-a=8,a=-3。
3.解答题题型的解答
例5,已知函数f(x)=lnx-。(1)讨论函数f(x)的单调性,并证明f(x)有且只有两个零点;(2)设x0为f(x)的一个零点,证明曲线y=lnx在A(x0,lnx0)处的切线也是曲线y=ex的切线。
该题目的第(1)问难度并不大,运用导数知识以及零点存在定理可证明。第(2)具有一定的技巧性,难度较大,应充分利用已知条件,采用设而不求的方法解答。
1不难得知x的取值范围为(0,1)∪(1,+∞)。则>0,则在(0,1)和(1,+∞)为增函数。分别令x=和x=,则f()=-1+<0,f()=ln+3>0,在(0,1)内有唯一零点。同理,分别令x=e和x=e2,不难证明在(1,+∞)内有唯一零点。(2)由已知可知lnx0=,曲线y=lnx在A(x0,lnx0)处的切线方程为y-lnx0=(x-x0),整理得到y=x+。设曲线y=ex在(x1,ex1)处的切线方程为y-ex1=ex1(x-x1)。令=ex1时,则x1=-lnx0,则y=ex的切线为y=x++lnx0,整理得到y=x+得证。
通过解答函数解答题可知,其不仅综合了函数基础知识,而且很好的考查了学生思维的灵活性。为提高该题型的解答正确率,授课中既要使学生牢固掌握各种函数的求导公式,又要具备灵活的头脑,认真审题,观察题目特点,争取找到简单又高效的解题思路。正如例5中在证明函数零点时恰当的设出了特殊点。另外,在第(2)问的证明中通过设出y=ex的切线方程,通过运用已知条件进行转化,降低了解题的难度。
三、结论
高中数学函数教学中,为使学生掌握相关题型的解题方法,在高考中顺利求解相关试题,既要做好高考中函数常考知识点的总结,又要认真分析相关的函数题型,使学生有针对、有目的性的学习。同时,注重优选高考中的典型习题,为学生讲解不同题型的解题思路以及解题方法,要求学生认真听讲,积极总结与反思,不断积累相关的解题经验,使其能够根据具体题型应用最佳的解题方法,实现函数试题解题效率的显著提升。
参考文献
[1]李啸骁.函数单调性的判定法及其在高考试题中的解题探讨[J].数学学习与研究,2019(22):115-116.
[2]李昭平.活跃在高考中的函数零点问题[J].高中数学教与学,2019(17):34-36.
[3]于丹丹,濮安山.高考中函数含参量不等式恒成立问题的解题[J].中学数学研究(华南师范大学版),2019(11):23-25.
