基于Simulink的多自由度系统振动仿真研究

黄兵 孔程程

摘要：多自由度有阻尼振动系统在工程实际中普遍存在，为研究和掌握该系统在外界激励作用下的振动规律，采用Matlab/simulink对多自由度振动系统进行仿真分析。数值仿真得到在正弦函数和固定值的外界激励作用下系统的输出性能，并研究不同的阻尼和弹簧参数对系统中质量块的位移和稳定性的影响。这对多自由度振动系统的实际应用提供参考依据。

关键词：simulink;多自由度;振动;仿真

0  引言

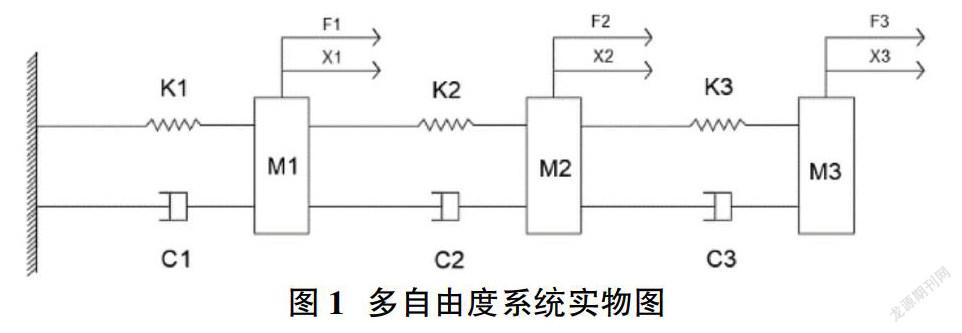
在实际工程中，许多物体都涉及到振动问题，比如在行驶过程中的汽车、城市轨道车辆、高速运行的动车等。但是对于很多复杂物体的振动分析较为困难，因此在分析的过程中要加以简化才可以。通常而言，大部分物体振动可以简化为简单的三自由度系统，这样更加方便计算和分析。比如现在的汽车在满足安全的同时追求更好的驾驶舒适性，其车的结构也是越来越复杂。大多数汽车座椅下面使用了弹簧和橡胶来吸收振动、缓解冲击，同时在汽车底盘和轮胎处都采用了减振装置，这所有就可以看成一个三自由度的系统。

简化模型来解决复杂振动问题，可以采用理论分析和数值仿真，数值仿真通常用Matlab。本文主要针对工程中常用的三自由度系统的简化模型进行了分析，综合采用理论计算和数值仿真。理论计算做了三自由度的运动微分方程、固有频率和主振型的计算，数值仿真做了系统的模型用来分析各部分在外界激励的作用下的位移响应曲线。本文用的是Simulink动态分析，它可以在做出实际系统之前，预先对设计的系统进行仿真分析，并可以根据仿真结果随时进行参数的修正，提高系统的性能和稳定性，以减少对实际系统的设计与修改，实现高效率的开发和设计分析系统的目的。

1  三自由度振动系统理论计算

本节用一个三自由度有阻尼系统来近似模拟简化的机械物体在运动过程中的振动。

问题描述：已知一个系统刚度K=500N/m，系统质量M3=20kg、M2=20kg、M1=20kg，阻尼器系数C=2Ns/m，弹簧和质量块为蓄能元件，阻尼器为耗能元件。三个质量块的位移分别为X1、X2和X3，外部激励X（t）为，系统初值为零。

具体分析过程如下：

根据对质量块受力分析，可以得到系统的动力学方程如下：

整理为下面的形式方便建模：

矩阵形式为：

即振动系统可以表示为：

下面进行系统的模态分析：

系统矩阵可以写为（4）

其中M-1表示系统质量逆矩阵，K表示刚度矩阵，可以表示为：

系统矩阵为：

令，则有

對此频率方程展开，令其为零，可得一个关于λ的方程，求解后得到系统的各阶固有频率：

D的伴随矩阵为

将代入式（6），可得

该矩阵是成比例的，矩阵的第三列就是取x1为基准的主振型。

同理，将带入式中，可得

将代入式中，可得

根据上面理论计算我们得到了三自由度的固有频率和主振型，得到固有频率和主振型可以了解到此系统的共振区域，通过对这些数据的了解与分析可知这系统设计的不合理处，为结构设计提供一定的指导，并在以后的振动损坏的起因上找到最不合理的地方并进行改进。也可以对计算模型进行校验，验证做的仿真计算的模型是否正确，为以后开展瞬态分析、谱分析提供基础。

2  Simulink仿真模型的建立与分析

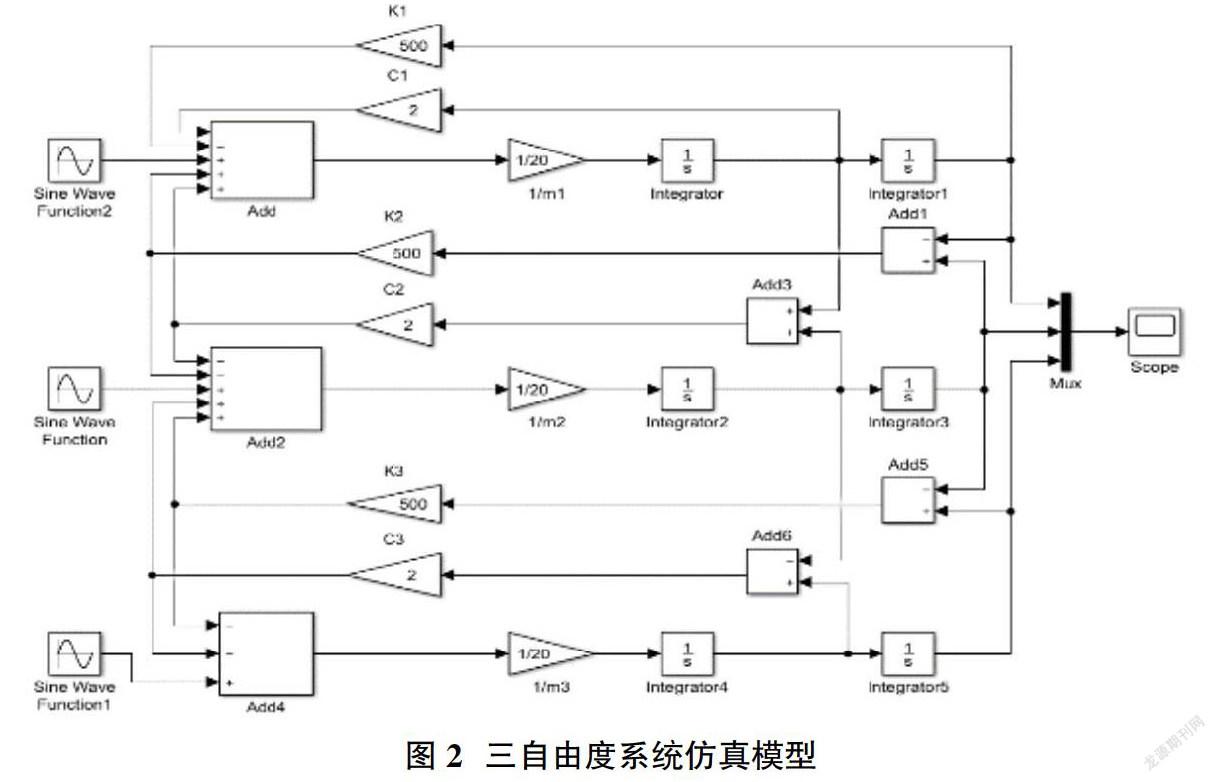
结合上述理论分析，采用Matlab/simulink对上述三自由度系统进行数值仿真，建立的仿真模型如图2所示。

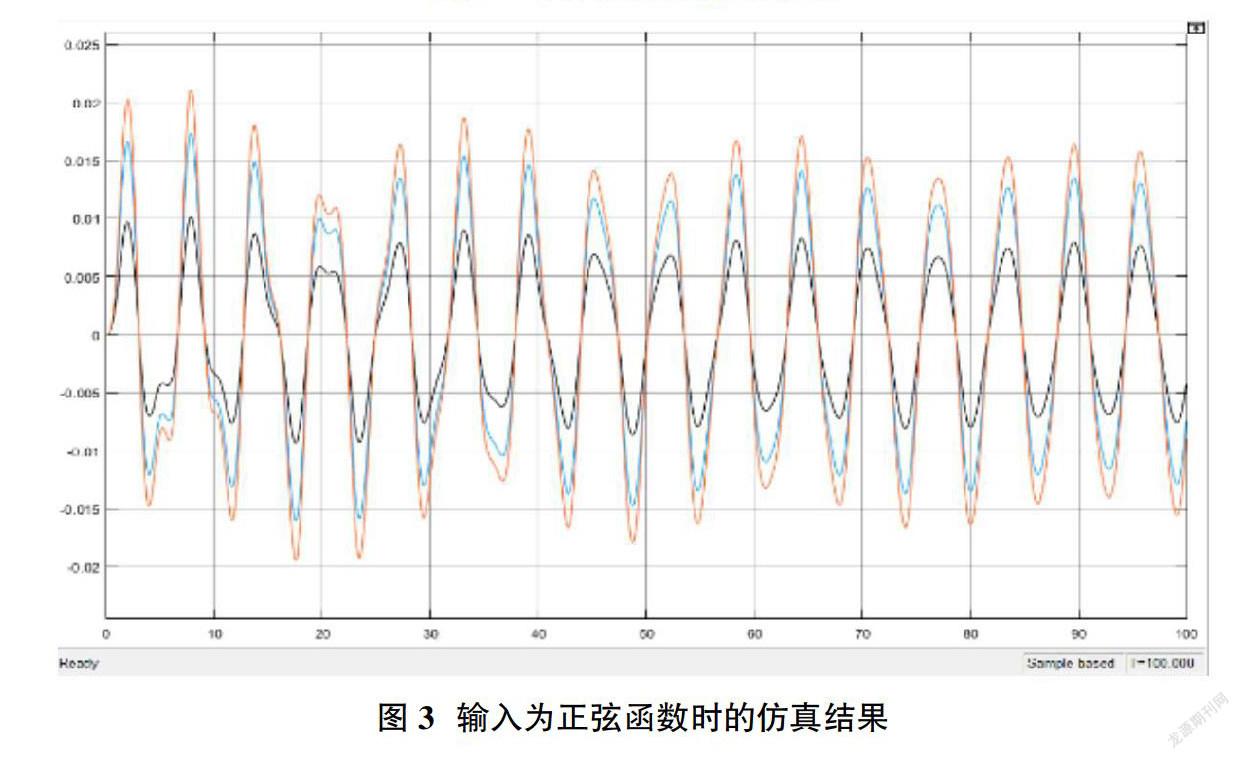
在该分析中，主要采用了增益模块、求和模块、积分模块、三角函数模块。分别设置一次和二次积分模块初始值为0，因为质量增益模块是在积分前面的，所以值要设为质量的倒数为1/20，最后分别设置刚度和阻尼增益模块为500和2。数值仿真结果如图3。

从仿真结果图可以看出当输入为正弦函数时，质量块的位移刚开始一段时间偏离平衡点比较远，而且振动不是很稳定，随着时间变化系统最终会以输入函数的形式在平衡点附近稳定的振动。当输入系统的外界激励是一个定值时，系统会在平衡点附近比较稳定的来回振动，最后因为阻尼作用而逐渐衰减为0。

3  结语

本文系统而简略地介绍了常见的多自由度数学模型的建立和Simulink的建模仿真。通过Simulink对设计的系统进行建模仿真，可以得到每个参数对系统的影响，并可以随时对不正确的参数进行优化，即先分析系统的可行性和可能产生的结果，然后在解决实际工程问题时能把设计的风险降到最低。这样可以更好的对系统设计提供理论基础，同时也可以对多自由度减振结构分析提供相应的参考和指导。

参考文献：

[1]陈作炳，刘颜.汽车多自由度结构振动分析[J].计算机与数字工程，2015，43（05）：841-843.

[2]扈静，袁中凡.基于SIMULINK的二阶、三阶系统建模与仿真[J].中国测试技术，2004（02）：20-21.

[3]王文娟.机械振动分析的Matlab/Simulink仿真研究[J].现代电子技术，2006（24）：46-48.

[4]单长吉.三级质量-弹簧-阻尼系统的特性分析[J].大学物理实验，2015，28（03）：35-37.

[5]刘鍊生，霍拳忠，黄克累.非线性振动系统主振型的一种求解方法及稳定性判定[J].应用数学和力学，1987（06）：505-512.

[6]冯奇，魏力.多自由度无阻尼机械振动系统各阶固有角频率与主振型的计算[J].机械设计，1989（04）：21.

[7]文涛，胡青春.基于MATLAB语言的多自由度振动系统的固有频率及主振型计算分析[J].中国制造业信息化，2007（01）：78-81.