系统思维 整体把握

摘要：课堂教学的改革要求教师以新的眼光审视“数学工具”的内涵，数轴作为一项学习工具，用直观而有效的方式带给学生解决问题的方法和思路。目前小学数学教学中对于数轴的使用现状却是流于形式，存在误区。如何适时、适度、适当地发挥数轴在教学中的价值？本文旨在厘清教育部审定（2013）人教版教材中“数轴”的使用素材梳理，结合自身的教学实践，对小学数学教学中数轴的使用进行一次探究，传承了数形结合思想，将数轴的内涵、应用价值与具体实践相结合，多方面使学生来感悟数轴这一学习工具对于建立数感、拓展思维的意义。

【关键词】数学工具; 数轴;数形结合; 数感

课堂教学改革给广大教师提出了许多新要求，我们教师要以发展性的眼光审读“数学工具”的价值取向。数轴是非常重要的数学工具之一，是学生进行数学学习活动的重要媒介。合理的使用数轴这一“数学工具”，能够很好的渗透数形结合思想，对学生数感的建立，数学思维的发展起到积极的作用。

一、“数轴”缘起——“一道习题”引发的思考

【镜头再现】

人教版一年级上册“11～20各数的认识”时，教材练习十七安排了这样的一道习题：

笔者在听课中发现：老师用的“填一填、对一对、读一读”是传统教学中的“三步曲”，教学效果不佳，导致很多学生不会填写。

简单的填数练习，为什么结果会如此糟糕。笔者课后翻读了教材内容，发现：这之前，教材没有单独介绍过“数轴”，学生很陌生，自然无从入手。

【课堂审视】在这堂课中，老师没有用活教材，没能让学生学会自己去深入思考，获得学习体验。课后笔者查阅了相关资料，产生了以下几点思考：

1.教师教法过于简单，忽视了培养学生探究新知的学习能力。学生对于“第一次”

接触有“数轴”的练习题应该是陌生而又充满学习兴趣的，而教师简单化的教学操作，只停留在“填一填，对一对，读一读”的层面，忽视了学生在“数轴”这个特定的几何图形上认识数的能力探究。笔者觉得应该要适时引导观察：“数轴上的几个数是怎样排列的？这些数排列的顺序与箭头的方向有什么关系？”。

2.习题价值挖掘不够，失去了发展学生高阶思维能力的机会。本道习题的意图在于

引导学生学会在数轴上观察数，体会数的顺序，感受到数的大小关系，而教师没有精准把握习题的意图和挖掘出习题的真正价值，停留在一个低级水平层次的教学，使得学生失去了高阶思维能力发展的机会。笔者认为，第一次教学这样的习题，如果精准了教学目标，挖掘了深层次的价值内容，定会提高后续教学的驱动能量。

二、聚焦“数轴”——“一套书”的整体解读

数轴作为一种特定的几何图形，是数形结合的重要载体之一。为了充分挖掘数轴这一直观形象的教学资源，笔者对“数轴概念”和相关“数轴习题内容”进行了全面解读和梳理。

1.“数轴”的概念解读。数轴是基本的数学工具，是学生形成认知、经历数学活动的重要媒介之一。教材中真正的数轴概念出现在初中一年级：“用一条直线上的点表示数，这条直线叫做数轴”。

2.“数轴”的应用价值。在小学阶段的学习中，学生或许并不清楚数轴的准确含义，但数轴早已和学生的学习形影不离。第一、借助数轴，学生能直观地感受数的排列是有规律和方向的，感受数的顺序性。第二、数轴上的“数量级”又能帮助学生认数、准确地判断数的大小。第三、将计数与数轴图像联系起来，学生能深入理解运算的性质，为以计数为基础的计算策略提供心理意象，渗透一一对应的思想。第四、数轴能体现间隔，并能使学生认识并判断位置与方向等。数轴具有形象地认识数的完备性的作用，有效使用数轴，对学生的数学思想、数学方法，甚至是数学能力的培养，发展数感都有着不可估量的作用。

三、巧用“数轴”——“数感”的实践思考

《义务教育数学课程标准（2011版）》指出：数感的主要表现是能用多种方法来理解并表示数的意义，能在具体的情境中，把握数的相对大小关系、表达和交流信息，能选择适当的算法解决问题，会估计运算的结果，并解释其合理性。

教材中的每条数轴都承载着提升学生数学思维的作用。在教学中，教师要深入理解数轴的使用价值，将数轴这一工具有意识地向学生逐步渗透，帮助建构认知，发展数感。

（一）点数对应，启蒙数感

1.依托数轴，感知数的顺序

数在数轴上的排列是有一定顺序，有一定方向的，这是学生建立数感的逻辑起点。借助数轴上的数序，学生通过观察对比，就能判断出负数总是比正数小;真、假分数所在的区间范围，决定了假分数肯定比真分数大;整数中位数多的数一定比位数少的数大等等。

比如：

在练习上面这道题时，教师并没有急着让学生填，而是先让学生观察已经给出的数，说说它们的大小，再觀察箭头的方向，引导学生发现，越往箭头方向，数就越大，从左往右，数是按从小到大的顺序排列的。然后引导观察“18”“19”两个数，明确单位长度表示“1”。在这样的理解下，学生填错的概率就很小了。反馈时，让学生自由表述解题的思考过程，理清思路，活跃思维。

生1：我知道10和12中间是11，所以第一个方框填11。

生2：我知道越往箭头方向越大，所以12后面肯定比它大，但是又比14小，所以只能填13。

生3：我知道17比18小1，所以它肯定填在18前面一格;19后面肯定是20，因为19加1是20。

......

2.借助数轴，理解运算性质

所有的实数都可以用数轴上的一个点来表示，利用这一性质可以帮助学生探究运算的算理，理解运算的性质，体会各种运算之间的联系与区别。

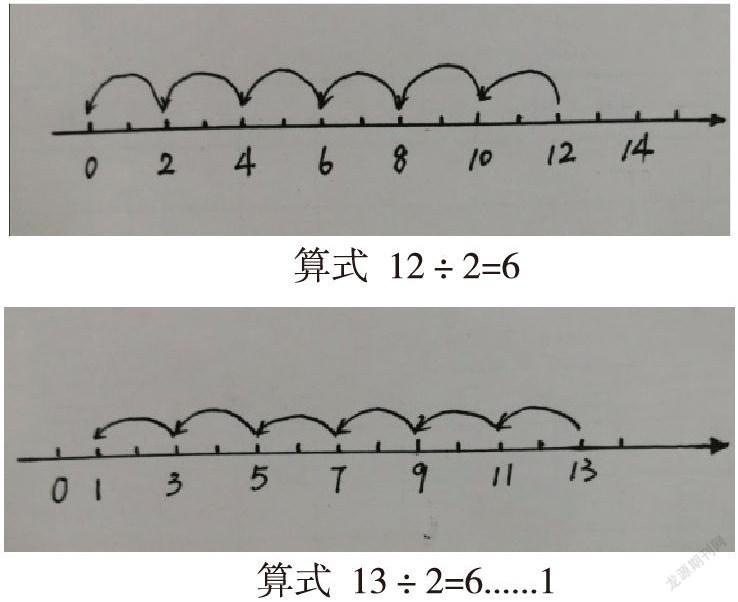
比如，除法可以看作是连续减去相同数的减法，就是在数轴上找到“被除数”，然后依次向左减若干个相同单位长度的数。如果减到最后恰好是0，就说明能整除，减的次数就是“商”，反之则是有“余数”，剩余几余数就是几。如下图：

算式 12÷2=6 算式 13÷2=6......1

点数对应，用图形化的方式表征运算的性质，不仅沟通了减法与除法的关系，更呈现了商及余数的来源，数轴的使用让抽象的计算变得有“形”可依，为学生多样化的计算策略提供了直观参照。

（二）借轴操作，发展数感

1.邻近原则，估算的意义一目了然

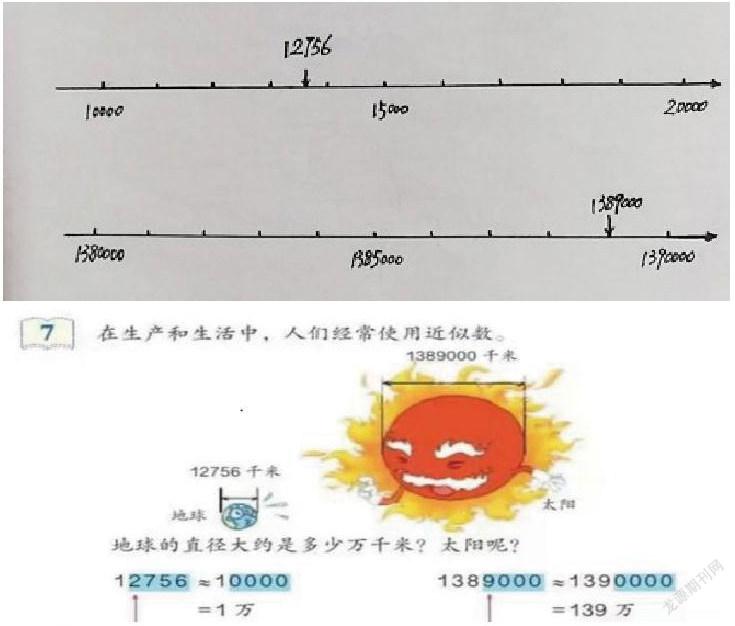
语文有预测，数学有估算，如出一辙，都是探索未知领域的法宝。“学生不仅要掌握估算的策略和方法，更要理解估算的意义，经历估算的过程，提升估算的意识。”数轴上的单位长度是确定的，借助这一特征，让学生在数轴上标出近似于某数的位置，是“四舍”还是“五入”就能直观地呈现在学生面前，“近似数”的概念就一目了然了。

如人教版四年级上册学习“近似数”时，课本上例7求地球和太阳直径的近似数，我们就可以借助数轴来帮助学生理解。让学生先找到12756在数轴上的大致位置，然后通过观察发现其更接近于10000，所以得到12756≈10000，而1389000则更接近于1390000，实质上是万位上的9通过“五入”得到的。通过直观的呈现，学生自然就理解了“四舍五入”的方法，也就能运用自如了。

2. 对称原则，负数的概念顺理成章

负数概念的出现，是学生认识“数”的一次飞跃，自此学生的认数范围拓展到了有理数。虽然学生在日常生活中已经不经意间接触过负数，比如零下的温度，电梯显示的地下二层等，但这只是停留在生活经验的感性认识，缺乏数学意义的理解。教学中，教师若能借助数轴引出负数的概念，那么学生的认识便会顺理成章。

教学片断：

师：你能在温度计上找出零上5度和零下5度吗？

生：0往上5格是零上5度，0往下5格是零下5度。

师：“0”的作用是什么？

生：“0”是分界点。

师：如果把温度计横过来变成一条数轴，你还能找到零上5度和零下5度吗？你有什么发现？

生：我会先找到刻度“0”，往左数五格是零下五度，往右数五格是零上五度。

生：它们刚好相反。

师：对了，两个看似相同的数字，前面加了不同的符号，意义就完全相反，数字前面加“+”（正号）表示正数，数字前面加“-”（负号）表示负数。

数轴不仅为学生理解概念提供了感性支撑，更让学生体验了“建模”的过程，提升了数学素养。借助数轴认识相反意义的量，对正负数概念的学习更直观，印象更深刻。

（三）梳理体系，渗透数感

1.层层递进，梳理知识

低年级的学生对于新知的学习往往是零碎、片面的，利用数轴可以把零碎的知识串联起来，使之系统化。比如《20以内数的复习》就可以分步进行、依次推进。

一条看似简单却内涵丰富的“数轴”把20以内的数的知识都串联起来，打破了“分裂”的复习模型，层层递进，面面俱到。

2.串线成网，形成体系

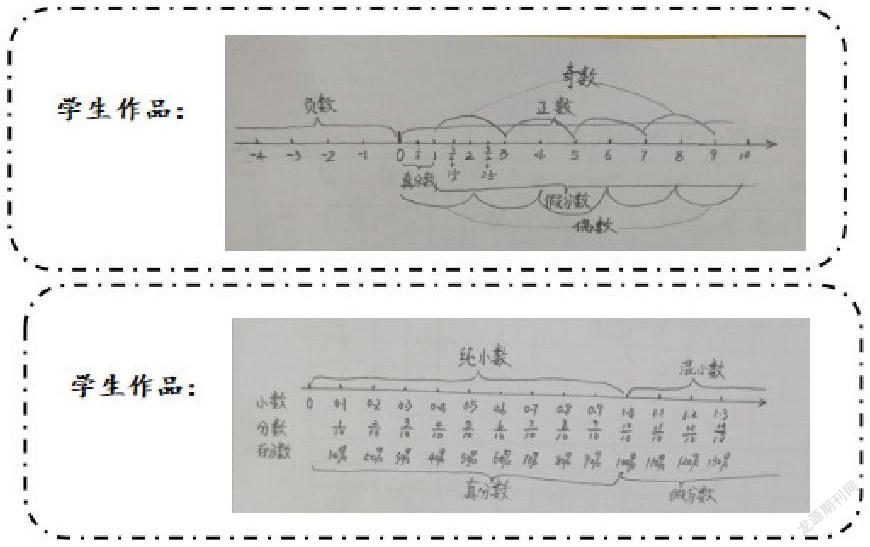
数的概念出现于小学各个学段，知识点分散，学生很难自主理清其中关系。笔者认为教学中可以利用数轴，穿针引线，系统梳理，形成整体。

把数轴作为切入点，展开数的总复习，把小学阶段关于整数、小数、分数、百分数的知识都“搬迁”至数轴上，不仅使原本分散的知识点得以梳理，也能在转化中感悟有些数虽然单位不一样，但它们表示的是同一个大小的数，由此发现这些数之间的关系。这样由知识“轴”构成的知识“网”，架起了学生认知的结构，形成了学习的网络，渗透了整体的数概念。

（四）迁移内化，体悟数感

1.纵横交错，感受对应

两条相互垂直且有公共原点的数轴就能组成一个平面直角坐标系，而用一对有顺序的“数”唯一地确定平面上的一个“点”，就能帮助学生在二维空间里确定物体的位置。

比如，五年级上学期学习《用数对确定位置》，让学生根据阳光小区的平面图用数对表示超市、书店，并依据数对在图中标出学校、诊所的位置：

利用数对到数轴的巧妙遷移，学生就能快速通过两个数据来确定物体所处的位置。

通过形来研究数的特点，通过数来呈现物体的位置，纵横相交的两条数轴，不仅培养了学生的空间观念，更让学生感悟到了一一对应的思想。

2.聚焦放大，体验无穷

在以往的教学中，“无限”的思想非常抽象，学生不易理解，数轴却能攻克这一难题。比如，在五年级学习了《分数的通分》后，教师可以设计“找一找”的游戏，激发学生在数轴上找到符合要求的数。

师：找出一个比2/3小但比1/4大的数。

生（思考片刻后）：2/4，1/3。

师：你们能在数轴上表示出来吗？

师：除了这两个数，还有其它数吗？

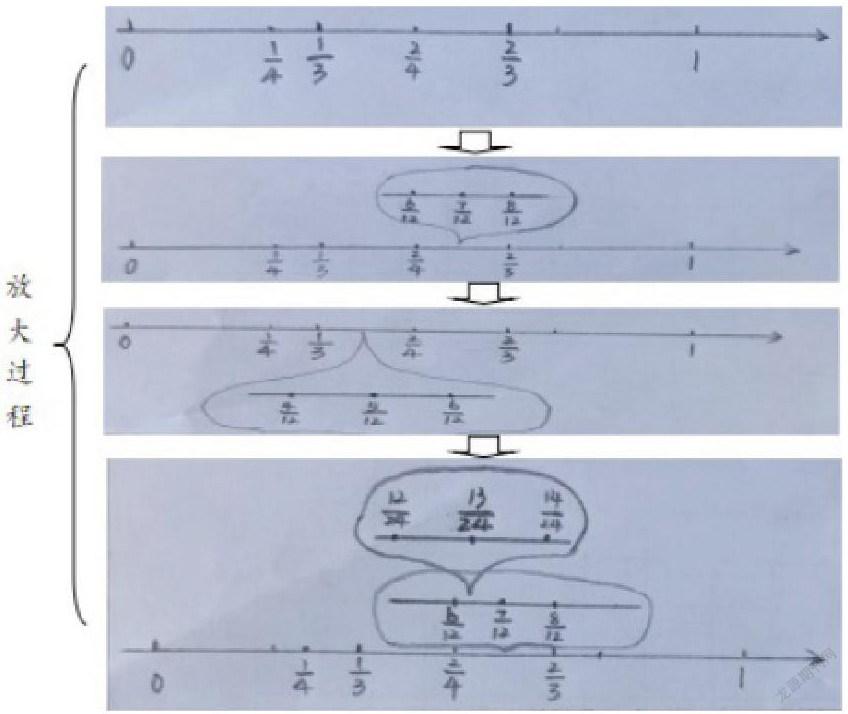
学生陷入了沉思，数轴上2/4，1/3的两边还有空隙，就“一定还有”，大家纷纷表示要把空隙的部分再“放大”，于是纷纷动起笔来：

层层逼近的问题让学生对数轴的使用产生了强烈的渴望。随着数轴的层层放大，学生惊喜地发现隐藏在其中的分数有无数个。这个找分数的过程极大地丰富了学生对分数的认识，深刻地感受了“无限”的思想，在头脑中初步建立起无穷这一宏观的数系结构。

教师要学会充分挖掘数学教材中的教学资源，精准把握教学目标，优化教学手段，巧借“数轴”这一学习工具，努力提升学生“数感”，培养探究新知的学习能力，为学生高阶思维的发展提供可能。然而数轴只是众多教学工具中的一种，也并非是建立数感、拓展思维的唯一途径。我们应该以新的眼光审视“数学工具”的内涵，让它们更好地服务于数学课堂。

参考文献：

[1]中华人民共和国教育部制定.义务教育数学课程标准（2011版）[S].北京：北京师范大学出版社，2012，1.

[2]王玉洁.试论北师大小学数学教材中的数轴使用方法[J].新校园旬刊，2016（7）：103-103.

[3]于蓉.关于教学中应用数轴的思考[J].课程教学研究，2015（8）：72-74.

[4]戴小军.巧用数轴，演绎精彩课堂—“数的认识总复习”教学案例[J].小学教学参考，2014（20）：27-28.

浙江省杭州市淳安县临岐镇中心小学卸岭完小 方海燕