CPFS结构理论及其对数学概念教学的启示

2020-09-10傅赢芳喻平

教育研究与评论（中学教育教学） 2020年6期

傅赢芳喻平

摘要：CPFS是数学学习者的一种特殊的优良认知结构。其中的概念域及概念系因刻画了数学概念间的等价关系及抽象关系，而区别于命题网络表征;概念域因与命题域的组织方式是相似的，而避免了同一概念从陈述性向程序性转化时面临的表征转换问题。基于CPFS结构理论，在数学概念教学中，应引导学生识别同一概念不同定义之间以及不同概念之间的演绎推理关系，直观化表示概念与命题的扩展过程，注意设置需借助概念域解决的问题串，引导学生选择概念的不同定义解决相应的问题。

关键词：CPFS结构概念域概念系命题网络表征概念教学

在影响学习的诸多要素中，认知结构是决定成效的一个关键因素。在学习心理学中，不同的研究者对认知结构的构成分析各有侧重。皮亚杰用图式来刻画学习者心理活动的框架或组织结构，图式的发展经历同化、顺应和平衡三个过程;奥苏贝尔则用可利用性、可辨别性及稳定性来反映个体认知结构的优良程度。这些都是从一般意义上讨论个体的内在心理结构。考虑到数学知识及其组织有其独特性，本文基于CPFS结构理论，论述其对数学学习的影响以及对数学概念教学的启示。

一、CPFS结构及其对数学学习的影响

（一）CPFS结构

CPFS结构是个体头脑中内化的数学知识网络，各知识点在网络中处于一定的位置，知识点之间具有等值抽象关系、强抽象关系、弱抽象关系或广义抽象关系。“CPFS结构是概念域（concept field）、概念系（concept system）、命题域（proposition field）、命题系（proposition system）的统称。”其中，概念域是指一个概念的所有等价定义的图式。在这组等价定义中，有一个最基本的定义——往往是教科书中的定义，称为该概念的典型定义。它的特点是最易于学生学习，同时又不失数学的严谨性。概念系是指个体头脑中形成的不同概念间的网络图式，这些概念间具有某种强抽象、弱抽象或广义抽象关系。

1.概念域与命题网络表征。

相比于命题网络表征的各种模型，概念域能更准确地贮存数学概念间的逻辑关系。对学习者而言，在概念获得与表征阶段，数学概念是被当作一种事实静态地对待的，属于陈述性知识。根据知识表征理论，其表征形式之一为命题网络。对于复杂的命题网络，Collins等人先后提出了层次网络模型与激活扩散模型，这两种模型分别以知识间的从属关系和语义关系来联结各个不同的概念以及概念的不同属性。层次网络模型明确了从语义记忆中检索信息的方式。语义记忆由巨大的概念网络组成;概念由单元和特征组成，并由一系列联想节点相连。层次网络模型主要揭示了陈述性知识间的纵向关系，而激活扩散模型则在层次网络模型的基础上，进一步刻画了知识间的横向关系。尽管后者能很好地描摹一般的陈述性知识的贮存形式，但是，数学中一种特殊且非常重要的等价关系却并不能在这个模型中得到体现。比如，“等腰三角形有两个角相等”（记为A1）、“等腰三角形有两条边相等”（记为A2）、“等腰三角形是轴对称图形”（记为A3）这三个特征，在命题网络表征中，仅仅作为“等腰三角形”的三个并列的属性来贮存。但是，从数学的角度来看，A1与A2是等价的，或者说，具有等值抽象关系，它们与A3属性完全不同，A3是等腰三角形的必要非充分条件，因此，在贮存信息时，它与A1、A2应具有不同等的位置。概念域将A1、A2从这一系列属性中区分出来，并形成数学学习者特有的表征形式，它弥补了用命题网络形式表征数学概念的不足。

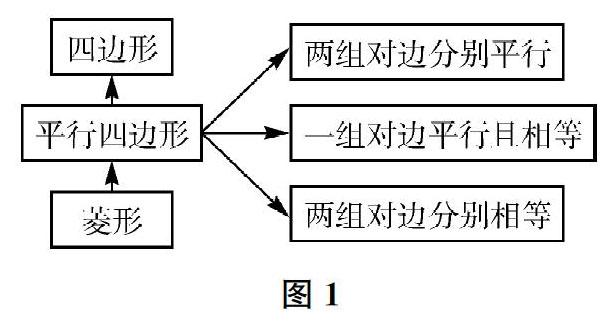
概念域的提出具有充分的理论与实践基础。概念域的核心关系——等价关系的识别与提取，一方面，源于研究者对学习者概念学习的观察与分析。在教学实践中，学习者学习了概念之后，在具体应用时会出现类型各异的错误，或是没有把握概念内涵，无法辨认概念的反例，或是不能理解概念的变式。另一方面，也基于数学概念自身的特点。同一个数学概念可以从不同侧面或角度去刻画，从而可以构成彼此等价的一组描述。比如，平行四边形概念的等价定义有：①两组对边分别平行的四边形是平行四边形;②一组对边平行且相等的四边形是平行四边形;③两组对边分别相等的四边形是平行四边形;等等。由于数学概念的发展性，等价定义还可以在不同的结构中进行刻画。比如，圆的定义，在平面几何中的形式为“平面上到定点的距离等于定长的点的集合”，在解析几何中的形式为“形如x2+y2+Dx+Ey+F=0（D2+E2-4F>0）的方程所确定的曲线”。

2.概念域與表征转换。

根据安德森的知识分类学，当学习者运用概念解决问题时，数学概念成为一种程序性知识。其表征形式为产生式系统，即由一系列产生式“如果……那么……”重叠而成。这与知识的命题网络表征结构完全不同。因而，当一个概念由前期的陈述性转为后期的程序性时，就涉及完全不同的两种表征形式之间的转换问题，给学习造成了一定的困难。这在数学概念学习的过程中表现尤为突出。同一个概念，学习的前后阶段，其知识性质发生了变化。比如，对于平行四边形的定义“两组对边分别平行的四边形是平行四边形”，在概念形成过程中，学生通过观察、概括一系列例子，归纳得到平行四边形具有的性质，并形成一种命题表征形式;但在知觉水平与思维水平的应用过程中，学生需要借助该概念进行图形判断或命题判断，此时，需要激活的是一种动态贮存形式——“如果两组对边分别平行，则这个四边形是平行四边形”。这就要求学生将前一种命题表征形式转换为后面的产生式。这种转换的需求和难度随着学习的深入，也在不断增加。比如，图1是将平行四边形作为陈述性知识贮存的命题网络片段;下页图2是将平行四边形作为程序性知识贮存的产生式系统片段。两者在结构上迥异，导致学生在解决问题时，激活与提取的速度产生差异。

在概念域中，概念的不同侧面或角度的表述是以等价关系来贮存的，其结构形式与命题域中的结构形式是对等的。因此，当一个概念随着学习阶段的变化，从陈述性转为程序性时，并不会带来表征转换的认知负荷。也就是说，相对于命题网络与产生式系统之间的转换而言，概念域与命题域之间由于逻辑上的同等，均为等价关系，可以很好地从陈述性知识形态转化为程序性知识形态。

3.概念系与命题网络表征。

数学概念还有一种特殊性，即在定义新概念时会用到已经习得的旧概念。为了能很好地将新旧概念间的这种关系刻画出来，喻平借助徐利治先生关于抽象关系的定义，进一步完善了不同概念间关系的组织与刻画。抽象关系包括强抽象关系、弱抽象关系以及广义抽象关系。如果从一个数学概念A中选取某一特征加以抽象，从而获得比概念A更广的概念B，使概念A成为概念B的特例，就称A到B的抽象为弱抽象;如果通过引入新的特征来强化原概念A，从而获得新概念B，那么概念B是概念A的特例，则称A到B的抽象为强抽象;如果在定义概念B时用到了概念A，则称A到B的抽象为广义抽象。由此，概念间的关系可以通过这三种抽象关系来概括。抽象关系扩张了层次网络模型中的从属关系或激活扩散模型中的语义关系。从属关系实际上对应于强抽象或弱抽象关系，但不能囊括广义抽象关系。

进一步地，是以数学化的方式来比拟这种结构。假设用Ri表示强抽象、弱抽象或广义抽象中的任意一种关系，用C1，C2，…，Ci，…，Cn表示存在抽象关系的一组概念，则C1R1C2R2C3…Rn-1Cn构成了一条概念链。如果两条概念链的交集非空，则称这两条概念链相交。如果m条概念链中至少有一条与其余的都相交，则称这m条概念链所组成的概念网络图式为概念系。因此，由抽象关系联结构成的概念网络更加立体、综合，从而更有助于学习者对相关概念的激活与提取。

实际上，网络中知识点之间的抽象关系蕴含着某种思维方法，因而网络中知识点之间的联结包含着数学方法，即“连线集”也是一个方法系统。以概念域来讲，它是由某一概念的一组等价定义构成的。等价与抽象关系不同，后者可以根据概念本身的结构——属加种差来识别，而等价关系的确立却是建立在逻辑推理的基础之上的。因此，从这个意义上来说，概念域中实际上包含着逻辑推理的方法。命题域、命题系的建构过程则更加体现了这一特点。

（二）CPFS结构对数学学习的影响

个体的CPFS结构与数学学习成就有密切关系。第一，个体的CPFS结构有助于数学理解。李渺从CPFS结构的前后变化阐述了它与数学理解之间的关系。第二，个体的CPFS结构有助于问题表征。喻平以高中3个年级的学生为被试，探讨个体的CPFS结构与问题表征之间的关系，发现个体的CPFS结构与问题表征之间有密切关系：具备良好CPFS结构的学生更能正确、合理地表征问题，从而更能有效地解决问题。第三，个体的CPFS结构与解题自我监控能力相关。另一项研究测查了学生的解题自我监控能力与CPFS结构，发现解题自我监控能力和CPFS结构有密切关系;CPFS结构和解题自我监控能力独立地影响数学成绩，CPFS结构相比于解题自我监控能力，对数学成绩的影响更大。第四，个体的CPFS结构显著影响解题中的远迁移。在解题迁移的研究中，发现数学解题中的远迁移与个体形成的CPFS结构密切相关，优良的CPFS结构有助于远迁移的产生。在该项研究中，研究者主要针对CPFS结构中的命题域及命题系进行了测量。第五，个体的CPFS结构与探究问题能力显著相关。喻平等人以江苏省常州市某高中一年级的学生为被试，分别测查了个体的CPFS结构及探究问题能力，发现两者显著相关，CPFS结构对探究问题的成绩有显著影响。研究进一步指出了外部调控与CPFS结构对探究问题的交互作用：在有外部调控的情况下，优良CPFS结构组和不良CPFS结构组的被试在探究中、低难度问题的成绩上有显著差异，在探究高难度问题的成绩上没有显著差异。

二、基于CPFS结构的数学概念教学

在概念学习中，学生如果不能全方位、多背景地深入理解概念，没有在头脑中形成概念体系，那么，一旦换一个侧面或角度阐述同一个概念，他们就会不知所云。实际上，概念的一个定义只是从一个侧面去刻画概念，具有一定的片面性，而要做到深入把握概念的内涵，就应当从不同的角度去认识，掌握这个概念的一组等价定义。基于此，喻平提出了一系列在概念学习中完善学生CPFS结构的教学策略：（1）注重从多个侧面、多个角度揭示概念的内涵，包括从多种背景、多重层次、多维结构揭示概念的内涵;（2）形成概念体系;（3）加强概念的应用。在概念域的形成方面，应揭示与某一概念等价的多种不同的存在形式。在概念系的形成方面，应从三个方面概括：其一，建立概念网络，可以用概念图的方法;其二，明示概念之间的关系;其三，揭示蘊含在概念体系中的数学思想方法。在概念的应用方面，既包含了知觉水平上的应用，也包含了思维水平上的应用。

从上述分析来看，无论概念域还是概念系，都不是在新学概念时能立刻达成的，其达成需要经历多次有意识地回顾与整理的过程。在回溯过程中，尤其要注意以下几点：

（一）识别概念间的演绎推理关系

概念域和概念系的发展不止囊括了语义关系或从属关系，还有一种重要的关系隐含在其中，即演绎推理关系。在概念域中起重要作用的等价关系，是同一概念不同定义间的演绎推理关系;概念系中类似于从相似三角形到全等三角形的定义，也是一种演绎推理关系。因此，教师在教学中，不仅要重视不同定义间的演绎推理关系，也要重视不同概念间的演绎推理关系。

比如，“全等三角形”与“相似三角形”的关系。

在现行初中数学教材中，全等三角形的定义是“能够完全重合的两个三角形”。此后，从两个三角形对应边的相等关系或对应角的相等关系来进一步刻画。因此，这部分内容学习结束后，可以形成一个“全等三角形”的概念域。

相似三角形的典型定义为“各角分别对应相等、各边对应成比例的两个三角形”。此后，同样是从两个三角形对应边的比例关系或对应角的相等关系来进一步刻画，从而形成一个“相似三角形”的概念域。

当学习者主动或经由教师的引导意识到，全等三角形与相似三角形都是在刻画两个三角形的关系时，自然就会产生一种比较。因而，进一步意识到，全等实际上是相似的一种特殊情形，即相似比为1。由此，可从相似三角形的角度来形成全等三角形新的定义。

再如，“等腰三角形”的认识。

等腰三角形的典型定义是“有两条边相等的三角形”，这是小学阶段学生就已经习得的内容。在初中阶段，学生首先习得“等腰对等角”的几何性质，进一步通过证明，以定理形式得到“有两个角相等的三角形是等腰三角形”，从而扩展了定义的侧面。同时，学生还习得了等腰三角形的“三线合一”性质。至此，教师即可引导学生思考：能否由“三线合一”来定义等腰三角形？這是一个演绎推理关系的识别过程。根据全等三角形的“ASA”判定可知，可以由“三线合一”来定义等腰三角形，从而进一步扩展了原有的概念域。同样，在学习线段的垂直平分线时，也可进一步扩展等腰三角形的等价定义形式。这实际上弱化了原来的“三线合一”定义，即只要“高线与中线合一”，就是等腰三角形。由此，可以进一步证明得到“高线与角平分线合一”“中线与角平分线合一”的三角形也是等腰三角形。

（二）直观化表示概念与命题的扩展过程

随着学习的深入与拓展，学生头脑中的概念也会经历一个不断扩充、逐渐变得复杂的过程。因此，教师在教学时，应注意从简单的结构单元开始，并直观化表示出来。

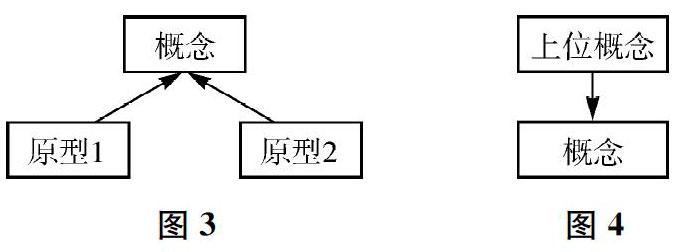
1.在概念形成阶段，用直观图式描述概念间的抽象关系。

在新授课中，教师往往处理的是概念的典型定义。如果是以概念形成的方式来获得概念，即由从特殊到一般的过程获得概念，那么概念与其现实背景或原型构成弱抽象关系;如果是以概念同化的方式来获得概念，即由从一般到特殊的过程获得概念，则概念与其上位概念构成强抽象关系。不管是以何种方式获得概念，在这一阶段都可以用直观的图式表达概念系的片段信息（分别如图3、图4）。

2.在概念发展阶段，用等价关系刻画概念间的内在联系。

在概念的练习或后续内容的教学中，会发现诸多与原有典型定义等价的表述。此时，教师需要让学生明确意识到这种等价性，可以与学生一起完成逻辑推理的过程，并最终用图示的方式表示出来。

比如“全等三角形”概念扩展的直观图，如图5—图11所示。

当数学学习从一个分支学科跃入另一个分支学科时，由于所讨论对象一致而工具不一，导致在不同结构中对同一概念形成了不同的定义形式。这就需要教师有这种敏感性，并能将其显性化地揭示出来。

（三）设置需借助概念域解决的问题串

如果说前面第二阶段是帮助学生形成概念域，那么，相应习题的练习则是进一步巩固与完善概念域。

比如，“绝对值”概念学习完成后，学生会形成如下层次1与层次2构建的概念域。

层次1（几何角度）：数a的绝对值是指数轴上表示数a的点与原点的距离。

可以设置如下两类形式的问题：（1）在数轴上距离原点2个单位长度的点表示什么数？即运用层次1的概念来解答;（2）一个数的绝对值是4，这个数是多少？则是基于层次2的概念来解答。

当教材缺乏某个层次的问题时，就更需要教师基于CPFS结构理论进行有意识的反思，并据此设置问题串。

（四）选择概念的不同定义解决相应的问题

理论上，如果一个概念的一组等价定义中的某一个定义能够解决一个问题，那么这组等价定义中的任一个定义都能解决这个问题。但是，用不同定义解决同一问题的难度可能是不同的。因此，解题者需要认真分析问题，激活概念域，选择最佳定义解决问题。比如问题：