“数列极限夹逼准则”微课教学设计

郑琴 张晴霞 陈亚丽

[摘 要]以高等数学课程中的“数列极限夹逼准则”知识点为例，针对微课教学独特的教学设计方式，通过对引例的分析和解决，激发学生战胜困难的决心，让学生感受探索知识、解决问题的乐趣，培养学生学习数学知识的兴趣;着重从分析教学目标、分解重难点入手，针对有限项的和及无穷项的和两种情形，提出通过放缩得到参照数列的几种方案，对有限项和的缩小项进行重点阐述，提出合理的缩小方案;使学生可以通过微课学习了解数列极限夹逼准则的思想来源、背景及蕴含的数学文化和思想方法，并学会用此定理计算数列极限。

[关键词]微课;夹逼准则;教学设计

[基金项目]2018年西南石油大学项目“‘移动互联網+背景下基于泛在学习视角的生态课堂建设”;2018年西南石油大学项目“高等数学课程思政示范课程”

[作者简介]郑 琴（1981—），女，四川成都人，博士后，西南石油大学理学院讲师，主要从事大学数学系列课程教学方法研究;张晴霞（1980—），女，湖北天门人，数学与应用数学博士，西南石油大学理学院副教授，主要从事大学数学系列课程教学与研究;陈亚丽（1979—），女，河南郑州人，硕士，西南石油大学理学院教授，硕士生导师，主要从事在线与移动交互学习环境构建、教育大数据分析与应用研究。

[中图分类号] G642[文献标识码] A[文章编号] 1674-9324（2020）32-0279-03[收稿日期] 2020-04-10

随着高校教育教学改革的不断深化，微课作为一种新兴的教学方式，正受到越来越多的关注。近几年，由高等学校教学研究中心举办的“全国高校数学微课程教学设计竞赛”反响强烈，涌现了大批优秀的数学微课作品。笔者连续三年参加该竞赛，收获颇多，现将曾用于参赛的“数列极限夹逼准则”微课教学设计思路及方法，与同行分享。

一、教学目的

1.了解数列极限夹逼准则的思想来源、背景及蕴含的数学文化和思想方法;会用此定理计算数列极限。

2.培养学生的抽象概括、探究等创新思维能力[1]。

二、教学思想

1.通过对引例的分析和解决，激发学生战胜困难的决心，让学生感受探索知识、解决问题的乐趣，培养学生学习数学知识的兴趣。

2.利用夹逼准则求数列极限的过程充分体现了数学的逻辑推理思想方法，体现了数学的理性与严谨。让学生学会运用数学的思维方式去观察、分析，面对实际问题能主动尝试着从数学的角度运用所学知识和方法，寻找解决问题的策略。

3.引导学生发现美好事物中蕴含的数学元素和哲学思想，让美育和智育的相辅相成，培养学生热爱生活热爱学习的正面情感。

4.采用已知推未知、猜想、类比等自然过渡的方法，帮助学生建立新旧知识的联系，减轻学生认知压力，体验解决问题的成就感，获得掌握知识的自信。

三、重难点分析及对策

1.通过引例说明根据之前的方法求解某些数列极限的局限性，分析现有知识不能解决问题的原因，提出本次课要解决的问题，激发学生克服困难、解决问题的决心。

2.阐述定理，指出应用该定理解决问题的重难点在于参照数列的选取。

3.针对有限项的和及无穷项的和两种情形，提出通过放缩得到参照数列的几种方案。对有限项和的缩小项进行重点阐述，提出合理的缩小方案。

4.采用启发式、探究式教学;力求创设“自主探究型”问题情境，引导学生主动思考。整个教学过程中，先从特殊到一般，由具体到抽象，由表及里、层层递进、步步设问，从而达到让学生理解并掌握知识点的目的。将传统意义下的“学习”数学变为“研习”数学。

四、课程思政切入点

1.让学生巩固极限概念所蕴含的辩证法哲学思想：“化复杂为简单”，“无限和有限、近似和准确、量变和质变”等范畴的对立统一，“变”与“不变”不是绝对的，在一定条件下，矛盾双方可以相互转化。

2. 本着“数学来源于实践、数学服务于实践”的理念，通过实际问题的引入和分析，让学生感受数学知识的重要性，体会数学的理性与严谨，激发学生学习兴趣。

3. 从生活素材入手，引导学生发现美好事物中蕴含的数学元素和哲学思想，让美育和智育的相辅相成，培养学生热爱生活热爱学习的积极向上的情感。

五、教学过程

由两则小笑话引出夹逼准则，激发学生兴趣：

同学甲说：“比我长得帅的有女朋友，比我长得丑的也有女朋友，由夹逼准则，我也一定会有女朋友。”

同学乙说：“元旦节要过，春节也要过，期末考试安排在元旦节和春节中间，由夹逼准则，期末考试一定过。”

两则笑话的选材立足于当前大学生都非常关注的恋爱及期末考试这两个话题，而笑话通过非常简洁幽默的语言瞬间抓住学生的注意力，中间又非常直观地体现了夹逼准则“夹”和“逼”的思想，使学生既对夹逼准则产生了兴趣，又能初步领会夹逼准则的思想及用法。

（一）问题的提出

分析下面两个引例，引导学生思考如何求解这样的问题，说明现有方法不能解决此类问题的原因，引出解决此类问题的工具就是数列极限的夹逼准则[2]。

引例1：

这是一个数列极限问题，我们将此数列通项做一下简

当n趋于无穷时，三项指数函数均趋于无穷，它们的和也趋于无穷，而指数n分之1趋于0，所以这实际上是一个“”型未定式，通过已学知识尚无法求解。

引例2：

引例2同样是求数列极限，数列通项是n项和的形式，当n趋于无穷时，每一项的分母都趋于无穷，因此每一项的极限都是0，但由于项数也是n，项数也在无限增多，因此计算这个极限不能简单地运用四则运算法则，认为每一项极限都是0，加在一起也是0，而是应该看成无穷多个无穷小量相加，实际就是“”型未定式，它的极限当然不一定是0。

设问：形如引例1和引例2这样的数列极限应该如何求解呢？由此引出解决此类问题的方法正是夹逼准则。

1.数列极限夹逼准则定理。讲述数列极限夹逼准则的定理内容，着重强调定理的两个条件，以及“夹”和“逼”的含义。阐明定理的使用过程中，最关键的步骤即为构造夹挤不等式，即找到符合定理条件的参照数列。

针对有限项的和及无穷项的和两种情形，提出通过放缩得到参照数列的几种方案。

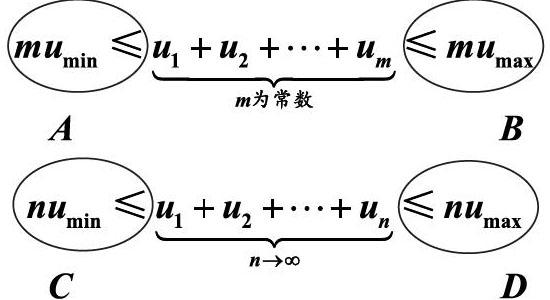
着重分析这样两种情形。第一种是针对m个正项的和，m为常数，也就是有限项和的形式。这m项加在一起的大小范围应该如何来确定呢？学生很容易想到它是小于等于m倍的最大，大于等于m倍的最小。再来分析n个正项的和，当n趋于无穷的时候的情形，这里的项数n虽然趋于无穷，但是这个和式的大小范围好像也遵从类似上面的规律，也就是小于等于n倍的最大，大于等于n倍的最小。那么就得到了针对有限项和无穷多项这两种形式的和进行放缩的几种方案，分别标注为abcd四项：

接着再引导学生仔细思考这四种方案是不是都合理呢？这里针对学生惯性思维常犯的错误，对A选项（有限项和的缩小项）进行重点阐述，特别指出合理的缩小方案不是m倍的最小项而是一倍的最大项。

下面通过非常简单直观的例子说明该方案的合理性：以一颗枣、一个桃和一个西瓜的总重量为例，如下图所示，这三个水果里最重的是西瓜，最轻的是枣，按照之前的理解，这三个水果的重量的和应该小于等于三个西瓜的重量，大于等于三颗枣的重量。

仔细观察不难发现，这样的估计并不合理，尤其当西瓜和枣的重量差别很大的时候，缩小后的三颗枣的重量与三个水果的实际重量可能会出现数量级的差别，而跟放大后的三个西瓜的重量差别就更大了。

如果将缩小的项改成一个西瓜的重量，如上页图所示。

一个西瓜显然更接近三个水果的总重量，跟三个西瓜比起来也只是倍数的差别而不存在数量级的差别。由此建立针对有限项及无穷项和进行放缩的方案，推出构造夹挤不等式的正确方法。

2.定理应用举例。根据前面讲解的找寻参照数列的方法，解决之前提出的两个引例。

（引导学生回忆之前推导的针对有限项和的放缩方法构造夹挤不等式，即小于等于三倍的最大，大于等于一倍的最大）

通过此题得出结论：对于形如引例一这样的有限个指数为n的指数函数的和开n次方再求极限的问题，极限就等于各指数函数项底数中的最大者。

根据之前推导的针对无穷项和的放缩方法构造夹挤不等式，即n项的和小于等于n倍的最大，大于等于n倍的最小。

六、小结与思考

本次微课设计介绍了利用放缩法构造夹挤不等式来求解数列极限的方法，针对几种不同类型的问题给出了具体的解决方案。

数列极限的夹逼准则在数列求极限问题中的应用十分广泛[3]，找寻参照数列的方法众多并且有的十分巧妙，可以让同学们下来以后查阅相关资料，自行研究和总结，还可以试着将数列极限的夹逼准则推广到函数极限的计算中去，得到函数极限的夹逼准则。

此部分还可留作思考题：思考如果将数列极限夹逼准则推广到函数极限夹逼准则，定理条件中哪些地方会发生相应的变化，应该如何修改？而函数极限夹逼准则的应用重点是否也是夹挤不等式的构造？针对函数的放缩方法又是如何呢？

此环节是课程最后一个部分—小结与思考。通过小结可以让学生厘清思路，明确重点，并且布置相应的任务可以为后续课程做好准备。通过解决思考题的过程能提高学生学习数学的积极性，培养学生的个人创新意识和创新能力，锻炼学生的逻辑思维、发散性思维和开放性思考能力。

参考文献

[1]龙志文.数列极限概念的新视角探析[J].教育教学论坛，2018， （48）：190-191.

[2]陈琳.微课教学在高等教育中的应用[J].教育教学论坛，2016， （08）：173-174.

[3]周淑娟，郭曉沛，李澎涛.浅谈N项和数列极限的几种求法[J].高等数学研究，2019，22（05）：7-8+47.