数学概念多元表征的教学活动设计及其反思

李冬梅 刘冉

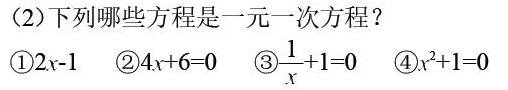
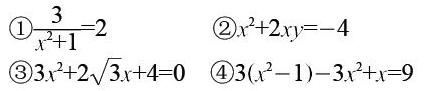
摘 要 数学概念是人们对数学关系和空间形式的抽象概括，它的特点就是概括性强、抽象度高，传统教学活动中单一的呈现方式不利于学生深刻理解概念的本质。本文提出基于概念形成与概念同化整合的教学活动设计，这样更利于学生对数学概念的理解，拓展思维空间，优化认知结构，提高学习的兴趣。另外，在运用多元表征理论进行数学概念教学设计时应注意学生的认知负荷和学情等。

关键词 多元表征 数学概念 概念形成 概念同化 认知负荷

中图分类号：G424                                 文献标识码：A  DOI：10.16400/j.cnki.kjdks.2020.05.044

Abstract Mathematical concepts refer to the abstract generalization of mathematical relations and spatial forms; It is characterized by strong generality and high degree of abstraction. The single presentation mode of teaching activities in the design does not make use of students deep understanding the essence of concepts. This paper puts forward the teaching activity design of the integration of concept formation and concept assimilation. It can promote students understanding the mathematical concepts， enhance the interest of learning， expand thinking space and optimize the cognitive structure. We should pay attention to students' cognitive load and learning conditions when we use the multi-representations to design teaching activities of mathematical concepts.

Keywords multi-representations; mathematics conception; conception form; conception assimilation; cognitive load

数学概念是人们对数学关系和空间形式的抽象概括，是建立数学公理、法則的基础，也是进行数学运算、推理、判断和证明的重要依据，更是展现数学思维、进行数学交流的重要工具。它具有高度的概括性和抽象性和一定的系统结构。[1]正是由于数学概念的这三个特点，造成教学中学生难以高效、准确理解与运用。

多元表征起初是由英国数学家迪因斯在上世纪60年代提出的多元具体化原则，该原则是指为了让学生建立抽象的数学结构，而呈现给学生具体的实物模型或者创设恰当的情境。数学概念的多元表征指通过运用多种表现形式表征数学概念，反映概念的本质含义，促进学生掌握概念的结构，内化概念的认知图式。它在教学中的作用主要表现在促进学生数学概念的理解，提升学习的趣味性;拓展学生的思维，促进积极认知投入;丰富学生的知识，优化其认知结构。

1 运用多元表征进行数学概念教学活动设计的过程

数学概念教学的本质就是教师通过实施有效的教学活动，促使学生能够概括出数学对象的共同本质属性，形成概念表象，理解数学概念的内涵与外延，建构良好的概念图式。教学活动设计在其中起到重要作用。通常学生理解概念主要是概念形成和概念同化两种方式，[2]在教学活动设计中，除了基于概念形成、概念同化的教学活动设计外，最重要的是基于概念形成与同化整合的教学活动设计。

基于概念形成与概念同化整合的多元表征教学设计，即综合考虑概念形成和概念同化的特点，并结合相关数学概念的特点，合理设计教学活动。其教学活动设计的过程：（1）复习旧知;（2）呈现新知的具体实例;（3）抽象概念实例的共同属性;（4）建立新旧知识的联系，深化理解;（5）运用概念。特别是在呈现新知的具体实例、抽象概括共同属性和建立新旧知识的联系三个环节中，教师要巧用多元表征，注重学生原有知识基础，观察分析概括概念的本质属性，建构新的认知图式。下面我们以一元二次方程的概念教学为例，说明如何进行概念形成与概念同化整合的多元表征教学活动设计。

1.1 复习旧知识

（1）以前我们学习过一元一次方程，请同学们写出一个一元一次方程，说出它的一般形式（  a≠0），并从中概括出一元一次方程的特点。

（2）下列哪些方程是一元一次方程？

在复习旧课环节，教师设计两个题目，题目1通过举例，让学生回忆一元一次方程的形式，并概括出它的一般形式，学生的思维经历了特殊到一般的形式，能够快速扑捉到一元一次方程的特点，快速推出它的一般形式。题目2是运用一元一次方程的概念进行判断，即能够运用概念做简单的分析判断。复习旧知识，这部分设计，主要的是为学习一元一次方程的概念建立联系、搭建支架，为同化新概念做铺垫。在教学活动设计的表征形式上，教师也运用情境表征、语言表征、模型表征等多种形式。

1.2 探索新知识

1.2.1 呈现问题

列出下面各题的数量关系式，并说说它们有什么特点？

（1）正方形桌面的面积是2m2，设正方形桌面的边长是xm，则边长与面积之间的数量关系怎么用方程表示？

（2）矩形花圃一面靠墙，另外三面所围的栅栏的总长度是19m，花圃的面积是24m2，设花圃的宽是xm，花圃的长是（19-2）m，则花圃的宽与面积之间的数量关系怎么用方程表示？

（3）长5m的梯子斜靠在墙上，梯子的底端到墙面的距离比梯子的顶端到地面的距离多1m，设梯子的底端到墙面的距离是xm，怎么用方程描述其中的数量关系？

1.2.2 独立思考

老师先让学生思考5分钟，独立尝试求解。

1.2.3 讨论分析

教师组织学生分小组交流合作讨论，建立同桌，前后位之间4人一个小组，就问题展开小组讨论，分析问题的思考过程，解答流程。教师可以依次与每个小组交流，查看学生的学习情况，针对学生的问题，并作必要的引导。

1.2.4 小组汇报

根据学生小组合作学习的情况，教师请各小组代表分别分享各自的答案，并就每个问题讲述下思考过程，教师并做引导与点评。

1.2.5 归纳总结

针对学生求解的方程，，，，引导学生化简方程，小组合作交流，看看这些方程有哪些特点？由学生总结出一元二次方程的含义，特点，教师做最后的重点说明，并就一元二次方程的一般式（a、b、c是常数，a≠0）中各部分的名称与系数做重点讲述。

1.3 巩固练习

当堂练习1：下列方程中哪些是一元二次方程？

当堂练习2：将方程化成一元二次方程的一般形式，并写出其中的二次项系数、一次项系数和常数项。

在探索新知识环节，教师设计三个具体的问题情境，通过组织学生思考，讨论，列出每道题的方程，然后观察、分析、讨论交流，归纳出一元二次方程的概念和特点，理解一元二次方程的一般形式，建构一元二次方程的认知图式。在整个教学设计中，通过小组合作学习，学生经历“独立思考—讨论分析—小组汇报—归纳总结”这一学习过程，培养自身数学抽象能力、数学建模能力和合作交流能力。

在巩固练习环节，教师设计两个题目，练习1是关于一元二次方程概念的判定，练习2是关于一元二次方程各个项与系数的掌握情况，通过上面的教学活动设计，这两个教学目标很自然的就能达到。在多元表征方法的运用上，两个教学环节中，教师采用了情境表征、语言表征、符号表征和模型表征等相结合，引发学生的认知思考，交流讨论，在小组合作交流中，更好地理解一元二次方程的概念，最终内化认知图式。此外，通过该教学设计，也反映出教学设计者背后的教学理念。在知识观上，反映出知识的获得是由学生基于原有的知识经验主动建构形成的。在学生观上，摒弃了传统教学中的直接灌输，反映出知识的学习并不简单由外到内的转移和传递，而是学生通過原有的知识经验同化新知识，丰富和改造自身知识经验。在教学观上，教学就是要激发学生原有的相关知识经验，促进学生知识经验的“生长”，教师的角色是一个引导者、促进者。

2 运用多元表征进行数学概念教学活动设计的反思

通过对以上教学活动设计的分析，我们自然有这样的疑问，运用多元表征法进行数学概念的教学活动设计时，我们需要注意什么问题？是否表征形式越多越好呢？我们觉得应从以下两个方面考虑：

（1）有效的教学活动设计取决于认知负荷。认知负荷理论是由Sweller等人证实并发展来的理论，认知负荷指工作记忆系统针对某一具体的学习任务进行加工和保持信息过程中所承受的负荷总量，它包括外在认知负荷、内在认知负荷、有效认知负荷。外在认知负荷指由于教师教学内容选择不当，教学内容组织呈现方式不当导致与认知加工过程无关的活动。[3]它指向教师所选择的教学内容与教学内容的呈现方式是否恰当。内在认知负荷指所学的内容材料本身所含有信息的数量以及各信息之间相互作用而对认知加工活动所产生的消极影响。它在一定程度上反映了学习任务的复杂性和难易度，学习任务越复杂，其产生的内在负荷就愈大。有效认知负荷指学生针对学习任务进行认知加工处理，建构认知图式的过程中产生的认知负荷，它指向于学生自身学习的过程。根据认知负荷理论，学生学习过程中产生的外在认知负荷、内在认知负荷与有效负荷三者负荷的总和应控制在学生负荷总量的最近发展区之内，有效的教学活动设计遵循的原则应该是降低外在负荷，内在负荷，增加有效负荷，引导以促进学生建构恰当的认知图式。

（2）有效的教学活动设计充分考虑学生的学情。既然认知负荷理论决定了教学活动的设计，所以依据认知负荷理论的基本观点，教师有效的教学活动设计必须充分考虑学生的学情。比如说学生的原有知识基础，数学逻辑思维水平和学习方式等等。只有充分考虑学生的学情，根据不同的学生学情，精选学习内容，优化教学内容的呈现方式，才能将外在认知负荷、内在认知负荷与有效负荷降到学生所成承受的最近发展区之内。

基金：湖南省2019年普通高校教学改革研究项目（2019-291-477）

参考文献

[1] 曹一鸣，张生春.数学教学论[M].北京：北京师范大学出版社，2010：144-145.

[2] 何小亚，姚静.中学数学教学设计[M].北京：科学出版社，2012：42.

[3] 唐剑岚，周莹.认知负荷理论及其研究的进展与思考[J].广西师范大学学报哲学社会科学版，2008（2）：76.