“定格”错误?摇 “变焦”思维
2020-09-10刘玉喜
刘玉喜
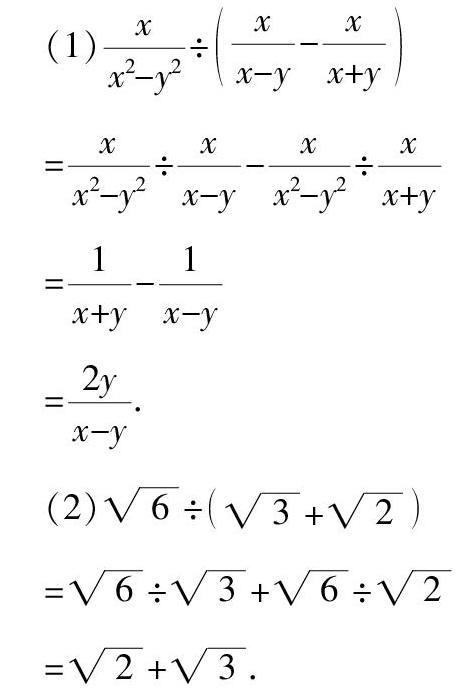
[摘 要] “错误是另一种美丽. ”数学学习中生成的错误具有独特的教育价值. “以错为源”开展教学,定格知识性错误、逻辑性错误、策略性错误和心理性错误,引领学生进行错误反思,可以帮助学生透过“错误”看到问题的“本质”,促使学生在不足中克服困难,促使学生在反思错误过程中实现错误思维纠正和转化.
[关键词] 初中数学;错误;反思能力;思维
戴再平曾说过“在学生解答数学习题的过程中,问题不在于是否存在错误,而在于教师应怎样正确对待学生的错误. ”教学实践中发现,针对学生出现的错误进行多次反复讲解与剖析,学生仍然会“一错再错”,究其原因是对错误缺乏深层次反思与总结,因此,必须引导学生学会对错误进行反思,将其思维引向深处,使其能发现错误产生根源及数学问题的本质,从而寻找到纠错的有效方法.
■ 反思知识性错误,优化学生基
础认知
数学教材中的概念、定理、运算法则、公式、性质等都属于基础知识,是数学解题的根本. 所谓“知识性错误”是指数学知识上的理解不清或运用不当而造成的错误,比如数学概念和性质混淆不清、忽视数学公式或定理成立的条件等. 教师可以抓住学生出现的具有代表性的知识性错误,引导学生反思知识点的内涵和外延,通过寻找知识联系,夯实数学基础知识,提高学生的解题思维水平.
例1 计算:
錯误解答:
反思过程:
师:你在做题时是如何思考的?
生:我用的是分配律,a÷(b+c)=a÷b+a÷c.
师:那你算下12÷(2+4)是不是等于12÷2+12÷4?
生:结果不一样.
师:那你回忆下我们学过的乘法分配律是怎么样的?
生:a·(b+c)=ac+bc.
师:乘法有分配律,但除法是没有分配律的,认真琢磨这两个式子就会发现意义完全不同.
反思总结 这两道题目错误的原因在于学生误用了乘法分配律,学生在计算过程中往往会为了计算简便,要么生搬硬套公式,要么随意创造出根本不存在的公式,比如除法分配律,一旦形成错误的思路,就会导致在后续的计算中也会出现同样的错误. 可见,只有让学生分析乘法和除法运算规则的本质,并有针对性地对其进行纠正,才能加深学生对数学知识的理解,避免再次犯错.
反思逻辑性错误,优化学生思维品质
数学是具有很强逻辑性的学科,其中,逻辑性最基本的表现就是公理. 同一律、矛盾律、因果律、排中律及充足理由律等是数学思维的基本逻辑规律. 所谓“逻辑性错误”是指在解题过程中因为违反了上述基本逻辑规律而导致推理的错误,比如,因分类不当,导致漏解惑错解;因不等价交换,造成解集扩大或缩小;因以虚假命题作为推理依据,导致虚假论证等等. 究其原因是学生在解题过程中过多地关注公式的选择或是解答的正确性,而忽视了题目中的数学逻辑关系. 因此,引领学生反思逻辑性错误,在揭示学生错误推理基础上,促使学生对错误进行批判性思考,使学生的思维品质得到进一步优化.
例2 已知■=■,求■的值.
错误解答:
由题意可得:x+1=2,2x+y+3=3, 解得:x=1,y=-2,所以,■=-■.
反思过程:
师:同学们对这种解法有意见吗?
生:错误. 只求出了本题的特殊答案.
师:那么该如何求解呢?
生:根据题意可设x+1=2k2x+y+3=3k(k≠0),解得:x=2k-1y=-k-1(k≠0),所以■=■(k≠0且k≠-1).
师:从以上解题过程你们可以发现什么?
生1:■=■,表示的是A和B的比值为■,而不是A=a,B=b,还可以是A=2a,B=2b,A=3a,B=3b…等等.
生2:不能以特殊性结论代替一般性结论.
反思总结 这道题错误的根源在于学生没有处理好数学问题中特殊性与一般性之间的关系,学生错在将一般性问题特殊化处理,属于逻辑性错误. 而这种逻辑性的错误就造成了解题的致命性错误.
反思策略性错误,优化学生解题策略
解题策略的选择直接关系着解题过程的繁杂、是否能得到正确答案. 所谓“策略性错误”是指在解题过程中因解题方法的偏差,导致解题难度增加或思路受阻,即使做对也是耗时耗力. 比如,在求解方程过程中,因变形不当导致计算过程相当烦琐,稍不注意就容易出现符号或数字错误. 选择一个好的解题策略,能够对提升解题效率起到事半功倍的作用. 因此,以策略性错误为源,引领学生在反思错误过程中将多种方法融为一体,并交叉使用,数学问题自然就能迎刃而解了.
例3 已知a=4+2■,b=4-2■,求a2b+ab2的值.
策略一:将a=4+2■,b=4-2■,直接代入a2b+ab2进行求解.
a2b+ab2=4+2■24-2■+4+2■4-2■2
=16+16■+84-2■+4+2■16-16■+8
=64.
师:上述解的结果有错吗?对这种计算方法你怎么看?
生1:虽然每一步都很正确,但比较浪费时间,且非常容易出错. 我有比较方便的方法:
策略二:先求出a2,b2的值,代入a2b+ab2进行求解.
a2=4+2■2=16+16■+8,b2=4-2■2=16-16■+8,
a2b+ab2=16+16■+84-2■+4+2■16-16■+8=64.
生2:策略二和策略一的解法大体一致,计算量仍然比较大,我还有一种简便的解题策略:
策略三:先将a2b+ab2进行转换得:ab(a+b),再代入a,b进行求解.
a2b+ab2=ab(a+b)=4+2■·4-2■4+2■+4-2■=(16-8)×8=64.
师:相比于策略一和策略二,明显策略三的计算更为简便,且计算量非常小,不容易出错.
反思总结 这是一道有关二次根式化简求值的题目,重点考查的是学生对乘法分配律的掌握和整体代入求值的思想. 从题目中给出的已知条件来看,策略一和策略二,虽然求解过程没有什么问题,但无形中增加了很多计算量,增加了学生出错的可能性. 策略三是此题最佳的解题策略. 通过有意向学生展示不恰当的解题思路,引發学生对解题策略和正确性的反思,从而充分调动学生寻找最优解题策略的积极性,达到优化学生解题策略的目的.
反思心理性错误,优化学生认知能力
所谓“心理性错误”是指在解题过程中,虽然学生已经具备了数学知识和技能,但因为审题错误、忽视隐含条件、疏忽符号变化、焦虑紧张、作答不规范、缺乏反思等心理因素而造成的解题错误. 在教学中,针对这类型错误,教师应引导学生反思错误原因,并适当指导学生审题,帮助学生养成认真审题的良好习惯及遇到困难问题不紧张的学习心态.
例4 已知关于x的一元二次方程(m2-1)x2+(2m+1)x+1=0有两个不等实根,求m的取值范围.
错误解答:
生1:根据题意方程有两个实根,所以判别式:
Δ=b2-4ac=(2m+1)2-4×(m2-1)×1=4m+5≥0,解得m≥-■.
师:其他同学得出的结果和他一样吗?结果是否正确呢?
生2:他忘记考虑一元二次方程的隐含条件“二次项系数不为零”.
师:原来忽视了一元二次方程的隐含条件. 生1你是否赞成生2的想法呢?
生1:我刚刚做题比较急躁,认为题目非常简单,没有考虑全面,要确保其为一元二次方程,还需要满足a=m2-1≠0?圯m≠±1,综上,m的取值范围应该是m≥-■且m≠±1.
反思总结 这一道题做错并不是学生数学知识和技能的缺乏,而是因为在解题过程中的一种急躁心理,导致他忽视了题目中的隐含条件,对问题考虑的不全面,从而造成解题错误,这是由于非智力因素而造成的过失性错误,属于心理性错误范畴. 作为教师,应从认真审题开始,通过科学指导,培养学生挖掘题目隐含条件和检验反思的良好习惯,从而有效提高学生的解题正确率.
结束语
“错误”的价值在于充分展示了学生解题思维过程中出现的纰漏,在纠错过程中引领学生进行反思,帮助其弄清错误实质,明确自身数学知识和方法缺陷之处,让学生在潜移默化中逐渐形成反思习惯,学会分析错误原因、归纳错误类型,这对于学生数学解题能力提升和良好学习习惯形成具有十分重要的意义.
