基于粗网格CFD模拟方法的室内空气污染物实时寻源反计算研究

（上海理工大学 环境与建筑学院，上海 200093）

0 引言

在现代社会中，人们在室内的时间达到了90%以上[1]，室内环境的空气质量安全显得尤为重要。污染物、火灾以及危险化学品意外泄漏等事故发生时，浓烟和毒气在短时间内扩散，此时需要快速定位污染源的位置，以保证人员的安全。

针对于如何快速、准确定位污染源位置的问题，反计算方法可以很好解决。通过分析探头处的污染物浓度信息和相应的气流组织，逆向推断出污染源的位置和释放时间。现在反计算已被广泛应用到相关实际问题中，比如将反计算应用于大气污染源位置的辨识[2-5]等相关研究之中；火灾发生时，通过相应的定位模型快速定位到火灾源头[6]。针对于反计算求解问题，Zhai将其归结为三类方法：正向求解法、反向求解法和概率反计算法[7]。

正向法是一种试凑法，假设所有可能的污染源位置和散发情况，并针对每种情况采用正向模拟求解计算结果，与实际情况最为相似的结果所对应的源的情况即为污染源位置最可能的解[8-10]；该方法效率低，耗时长。反向法从最终污染物的浓度场开始，采用负时间步长对污染物的扩散进行反推，最终获得污染源的位置[7]；该方法需要有最终浓度场所有的信息作为输入条件才能求解，在实际中这些信息很难被监测到，导致该方法使用的场合受限。概率反计算法则是采用概率分析估算某一事件作为概率目标函数，通过最大或最小化该目标函数来确定污染源的相关信息[11]，这种方法相比较于前两种，在运算强度、输入信息以及计算的稳定性方面都有明显的优势；Liu等已通过该方法成功定位到室内污染源的位置[12-13]。

然而，上述的方法虽然有着较好的精确性，但在实时性方面却表现的不理想，主要是由于CFD模拟获得气流场的时间很长，特别是对于非稳态的流动问题。人们开始研究如何提高模拟速度，一些学者提出使用简单的湍流模型[14]、采用先进的模拟软件和硬件以及使用粗网格模型[15]等方法。其中，网格密度和分布是影响CFD模拟时间的关键因素，对模拟的结果也有较大的影响[16]。在室内污染物寻源反计算的过程中，通常采用网格无关解进行模拟，以准确定位污染源的位置，而在实际情况中，受到计算机存储量、计算速度的限制，网格数量不可能无限大[17]。有研究显示，一个机舱模型在使用RANS湍流模型进行CFD计算的情况下，当网格数精密到可以准确模拟出机舱内非稳态气流组织形式的时候，使用k-ε模型所需时间大约为11 h，使用其他更为精密的模型则需要2倍甚至更久[18]。CFD模拟通过增大网格数量来对区域内的气流场和污染物扩散进行较为精确的描述，耗费了大量的时间。在室内污染物寻源反计算中，计算时间过长对于迅速定位污染源位置十分不利，因此需要研究一种快速有效的方法。相关文献中表明，网格划分的数量越多计算精度就越高，但工作量就越大、仿真分析效率就越低，所以不能采用无限增大网格数的方法来提高计算精度[19]；在CFD模拟中粗网格计算得到的结果与网格无关解的相差不大，并且可以大大减少运算的时间，假设网格无关解为1个单位的计算时间，则粗网格的计算时间要小于1%[16]。因此应该在保证精度的情况下尽可能的减少网格数，以快速定位污染源的位置。

本文考虑到在实际情况中污染源实时定位对时间的要求，研究粗网格在污染源定位中的准确性。网格数量的减少会引起流场计算的误差增大，但联合概率密度法对气流场数据的精度要求不是很高，因此本文主要验证了流场精确度下降后的定位准确性，从而在实际工程中可以减少污染物寻源的时间，实现实时定位。

1 研究原理

1.1 控制方程介绍

本研究中污染源定位模型主要是通过CFD粗网格模型数值模拟的方法验证其有效性。

控制方程的通用形式：

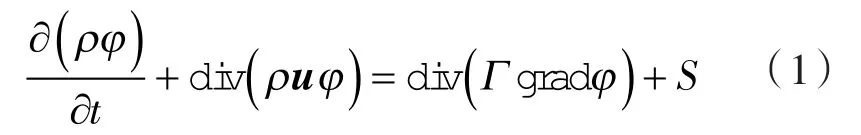
式中 ∂(ρφ)/∂t——瞬态项；

φ——通用变量，可以代表速度、温度，或是其他待求解变量；

div(ρuφ)——对流项；

di (Γgradφ)——扩散项；

Γ——广义扩散系数；

S——广义源项。

对于不同的控制方程，φ，Γ和S分别具有不同的形式。

1.2 污染物寻源反计算

污染物寻源反计算本质上是污染物传播特性的研究，通过相应的程序将动态气流场的方向取反，在探测器所处位置释放瞬时污染物，污染物将通过方向取反后的动态气流组织进行传播，在相应的时间内传播到真实污染源的位置，然后依据污染物正向传播时监测到的污染物浓度数据，结合概率分布理论求取污染源位置在整个空间区域的概率分布，其中概率值最大的点所对应的位置即认为是污染源位置[20]。

本文采用概率反计算法，以寻找源的位置展开研究。在矩形区域中的任何位置只要有污染物存在都可以认为其是潜在的污染源的位置[21]。概率反计算的表达式如下所示：

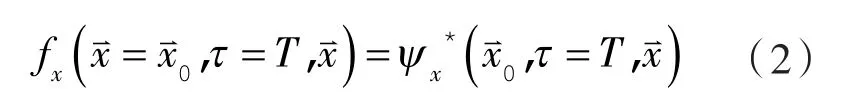
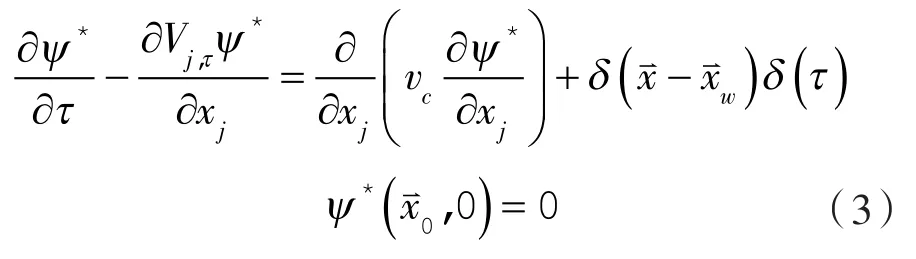
式中ψ＊—,—伴随概率因子；

τ——逆向时间；

Vj,τ——表示某一时刻τ的气流场；

vc——污染源在空气中的有效扩散系数；

δ（x）——脉冲函数；

利用探头监测到的污染物历史浓度信息来提高污染源定位的精确度；其具体的表达式如下：

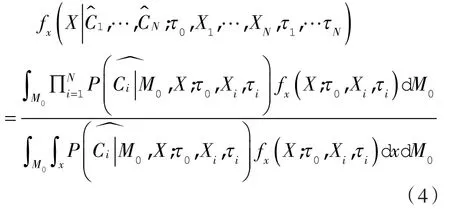
式中 N——探头处监测到的浓度数据的个数；

τ0——污染源的释放时间；

M0——瞬时污染源所释放的污染物质量总量；

fx（X；τ0，Xi，τi）为第i个监测探头的SALP；为根据多个探测数据计算得到的基于污染物的释放质量M0和位置处的概率分布。

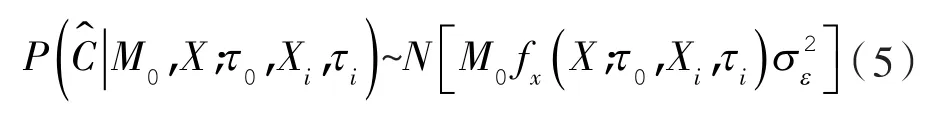
通过求解式（4）、（5）可计算得污染源的概率联合分布（CALP）。

为求解污染源位置的CALP，需要先求解得到污染源位置的SALP。求解SALP需要2个必要信息：非稳态的速度场以及在室内环境中布置的探头位置。其中，从式（3）中可以发现，式中的Vj,τ表示某一时刻的气流场，本文中污染源所存在的非稳态气流场是随时间变化的，因此网格的数量将影响计算的速度；采用网格无关解进行计算时，要耗费大量时间，若在保证寻源结果准确的前提下，在网格无关解的基础上减少网格的数量得到粗网格，将会大大缩短寻源计算的时间。所需要的非稳态的速度场、污染物扩散的浓度场均可通过CFD求解得到。

针对不同的具体案例，首先需要根据案例的具体参数进行建模，确定所设探头的位置、数量及其他物理参数；随后分别对网格无关解和粗网格模型进行CFD模拟，得到相应的动态气流场；然后将动态气流组织数据和探头在不同时刻监测得到的污染物浓度信息作为输入信息，输入反演计算程序。反演计算程序通过求解上文所阐述的公式，计算出污染源位置的伴随概率（SALP）和联合概率（CALP）。图1示出基于CFD污染源定位反计算的流程。

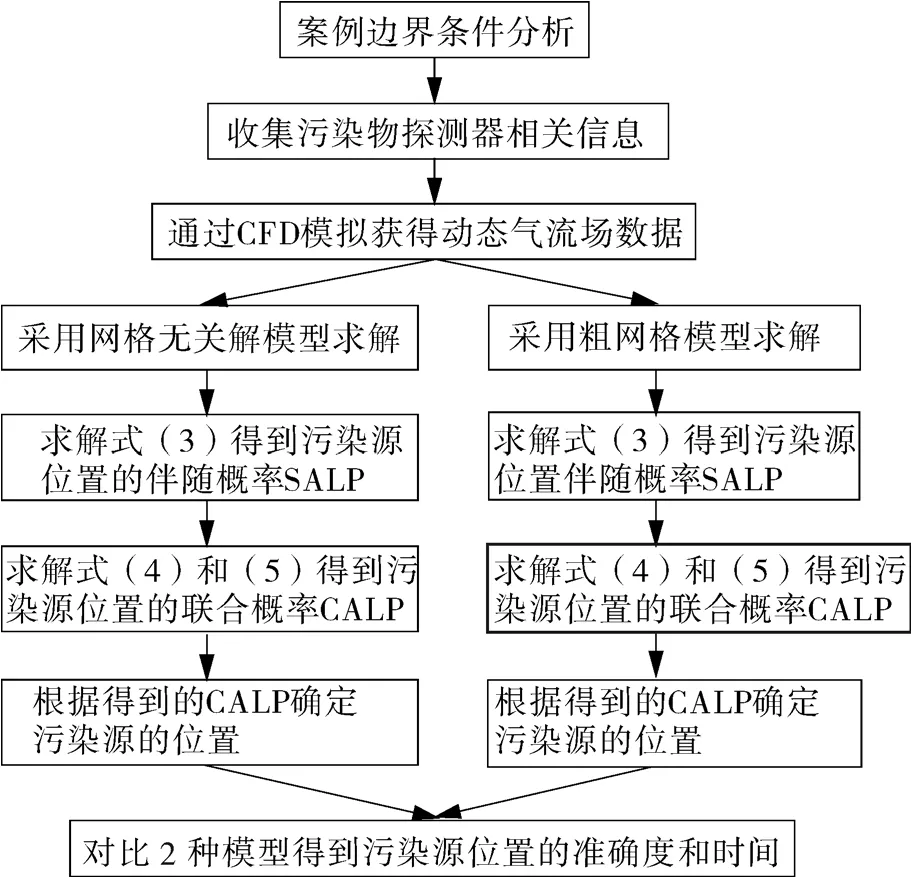
图1 基于CFD污染源定位反计算流程

2 案例验证

本文选用一个简化的二维办公室模型来验证上述的理论。由于办公室空间相对封闭，假设有污染源存在，若不能快速定位，后果将不堪设想。在此前的研究中，就已经在网格无关解的模型下使用概率反计算法精确的定位办公室污染源的位置，但耗费大量的时间，在实际中对于人员的安全十分不利。因此，在办公室模型网格无关解的基础上减少网格的数量，建立快速定位的粗网格模型。

办公室的长为10 m，高为3 m，假设办公室内有1人，1张桌子，桌子上放置1台电脑，人坐在电脑前面办公。其中假设人的发热量为70 W，电脑的发热量为200 W，在左墙的上方有一个水平条缝型送风口，送风速度0.1 m/s，送风温度T=20 ℃。右墙的下方设有一个水平条缝型出风口。

在办公室内安装2个污染物监测探头：探头1被安装在天花板中间位置，探头2被安装在办公室右上角。假设在窗户下方有一个瞬时释放的点污染源，源的大小为100单位。在t=0时刻开始释放，与此同时空调开启，送风口开始送风，在污染物的释放过程中，空调的气流组织还未达到稳定状态，时刻发生着变化，是一个典型的非稳态气流场。探测器从t=0时刻开始监测其周围环境污染物浓度的变化，直到整个过程结束。整个模拟过程持续240 s，分为8步，时间步长为30 s。采用Phoenics软件，湍流模型选择标准的k-ε模型。

图2 办公室模型在测线A处不同网格下的CFD数值模拟速度结果

2.1 网格数量的选取

针对该模型，本文分别设置了5种不同数量的网格，分别为 15×15，30×30，50×50，80×80 以及100×100的网格，首先进行网格无关解的计算，然后以此为基础确定粗网格模型。在办公室模型的中间位置（5 m处）设置了一条测线A，在测线A处记录不同时刻气流的大小。这5种网格在测线A处的计算结果如图2所示。

从图2比较5种网格数模拟结果，可以发现50×50网格、80×80网格和 100×100网格的差异较小，尤其是80×80网格和100×100网格的计算结果非常相似，可见80×80网格足以较好地描述该模型内部的流动特征，且在网格数增多的时候，模拟得到的非稳态气流场不再发生显著的差异，因此可认为80×80的网格为网格无关解。

2.2 粗网格模型污染物寻源的准确性

通过上述办公室模型中测线A处的不同时刻气流场大小的分析，发现30×30的网格相对于网格无关解，可以粗略地描述其速度场。对不同网格数获得的气流场进行寻源反计算，并比较30×30的网格和网格无关解的污染源定位结果，验证粗网格模型对污染源定位的准确性。

图3示出探头1多个污染物浓度数据联合探头2多个污染物浓度数据作为污染源定位的输入部分，通过定位模型的反计算得到污染源的位置。通过对比图3，发现两者的定位结果差异很小，都可以十分准确地定位到真实污染源的位置。即使是在30×30的网格下，其预测可能是真实污染源的位置也集中在很小的区域，较为集中，准确性较高。在30×30的网格中，通过污染源定位模型计算得到的有可能是真实污染源的位置的最高概率也高达90%，非常接近真实污染源所处的位置，所以通过30×30的网格模型可以进行准确的定位。因此，选取30×30的网格为粗网格。

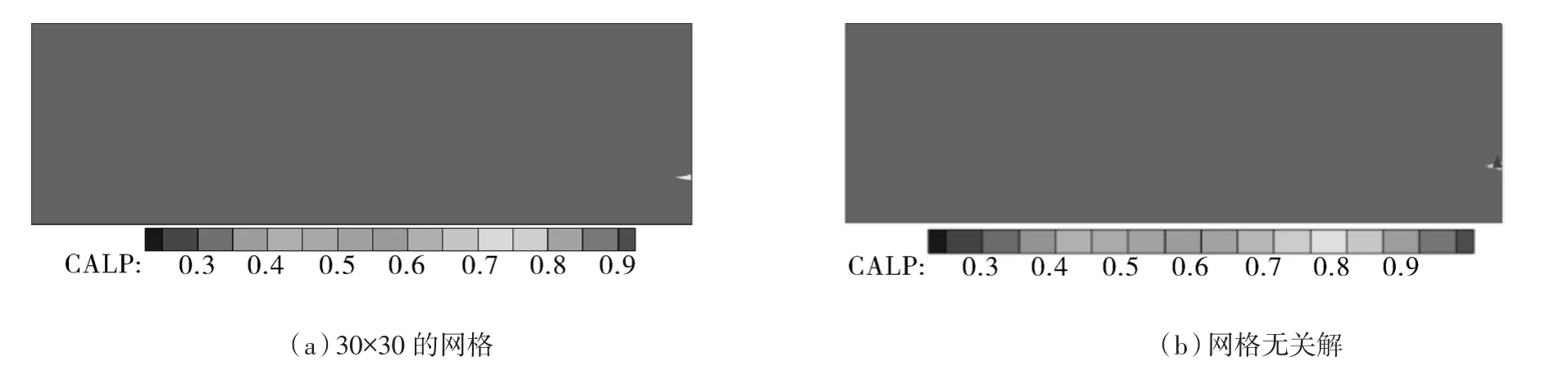
图3 探头1多个污染物浓度数据联合探头2多个污染物浓度数据CALP定位结果

3 粗网格模型讨论

通过以上粗网格的污染物寻源反计算，可以发现粗网格可以对污染源进行较为精确的定位，对此，为了进一步验证粗网格模型可以准确定位污染源的位置，比较 15×15,30×30和80×80的网格模型的速度场。

已知80×80的网格为网格无关解，30×30的网格是所选取的粗网格，在网格无关解下通过CFD模拟得到的速度场能够准确地描述办公室模型内部流动特征，以其为基准，并以此来比较15×15网格和粗网格下的速度场，对比分析三者速度场主要涡流的大小和方向，从而验证粗网格是否可以准确的定位真实污染源的位置。不同网格数的速度场如图4～7所示。

图4 t=60 s时刻速度云图

图5 t=120 s时刻速度云图

图6 t=180s 时刻速度云图

图7 t=240 s时刻速度云图

通过图4～7各个时刻的速度场云图对比分析可知，15×15网格由于其尺寸相对较大，造成其速度场的主要涡流和网格无关解的差距比较明显，尤其是在靠近进、出风口处；相比较而言，所选取的粗网格的主要涡流的大小和方向都和网格无关解的速度场的十分相似，没有明显差别，可以确定粗网格是可以对污染源进行准确的定位。

通过以上的分析，确定本文选取的粗网格可以准确的对污染源进行定位。最后，通过统计不同网格使用CFD模拟得到速度场所需要的运行时间，结果见表1。

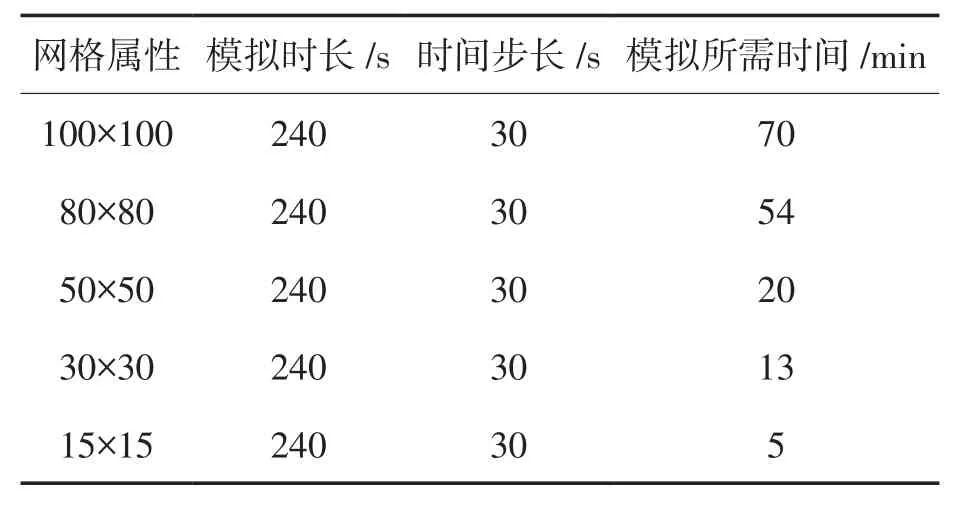
表1 不同网格下CFD模拟求解所需时间对比

计算采用的电脑型号为联想ThinkPad SL410，处理器为英特尔酷睿2双核T6570@2.1GHz笔记本处理器，内存为4 GB（尔必达DDR3 1066 MHz）。

从表1中可以发现，15×15网格下CFD模拟求解速度场所需要的时间最短，为5 min，但15×15的网格由于其网格尺寸较大，对细节的特征描述不够，相较于网格无关解的速度场相差较大，不能准确定位到污染源的位置。80×80的网格无关解与30×30的粗网格污染源定位结果相似，都较为准确，虽然网格无关解描述的速度场更加接近真实情况，但是其求解速度场需要耗费大量的时间，不能实时求解；而对于30×30的粗网格，计算时间缩短的同时又可以十分准确地定位污染源的位置。

仅是正向速度场计算的时间，粗网格模型就相较于网格无关解节约了70%以上的时间，完整的反计算要在此基础上进行速度取反后，计算伴随概率SALP和联合概率CALP，要耗费更长的时间。

4 结语

本文通过二维典型送风模型，利用不同网格数CFD模拟获得的气流场进行寻源反计算，以网格无关解的定位结果为基准研究粗网格寻源定位的准确性。可以发现，粗网格模型在非稳态气流场中可以准确的定位污染源的位置，而且仅与网格无关解的定位结果存在微小的误差，可以忽略不计；使用粗网格模型进行CFD模拟相较于网格无关解节约了70%以上的时间，提高了计算速度，可在非稳态气流组织工况下快速定位到污染源的位置，为后续的救援赢得宝贵的时间。