基于PSO算法的滑片-滑槽摩擦模型的参数识别分析
2020-09-10耿葵花李辛沫王少伟耿爱农
韦 为,耿葵花,李辛沫,王少伟,张 通,耿爱农
(1.广西大学 机械工程学院,南宁 530004;2.广西制造系统与先进制造技术重点实验室,南宁 530004;3.五邑大学 机电工程学院,广东江门 529020)
0 引言
大多数机械系统都是由运动副和构件组成,运动副内部存在不同程度的有接触关系的相对运动,由此产生的摩擦问题将无法避免。针对动态运动过程的摩擦问题建立的动态摩擦模型主要以LuGre摩擦模型为代表,Canudas[1]提出的 LuGre摩擦模型获得了广泛认可。LuGre摩擦模型可以对预滑动阶段的静摩擦与动摩擦之间转化的过程进行比较全面的描述。由于LuGre摩擦模型具有非线性特征,使得其模型的动态参数和静态参数的识别仍然具有较大难度[2-5]。
LuGre摩擦模型在很多方面都有应用。熊璐等[6]基于LuGre模型对摩擦非线性进行补偿,设计了压力自适应控制器;李琳等[7]使用Lugre摩擦模型对机器人关节摩擦力进行描述;郭丁旭等[8]并联机械臂动力学模型中引入LuGre摩擦模型来描述伺服关节内部的摩擦行为;魏琼等[9]结合LuGre摩擦模型,采用双观测器估计摩擦力模型中的部分不确定性参数;王晓军等[10]基于LuGre摩擦模型和线性互补问题(LCP)的数值算法,给出了具有双边约束含摩擦滑移铰平面多体系统动力学的数值算法;叶超等[11]基于LuGre模型对伺服系统摩擦进行补偿;赵惟玮等[12]基于LuGre摩擦模型对液压缸爬行现象进行了分析;郭远韬等[13]基于LuGre摩擦模型对转台伺服系统自适应摩擦进行补偿;王晓军等[14]对Coulomb干摩擦模型与LuGre摩擦模型进行了比较分析;李明等[15]提出了一种改进遗传算法对LuGre摩擦模型参数进行辨识。从这些研究通过建立LuGre摩擦模型来对不同研究对象进行分析,但是LuGre摩擦模型的准确建立仍然具有相当难度。
滚动活塞压缩机在制冷行业中有广泛的应用,压缩机的滑片在滑槽中做高速往复运动,且运动距离较短。针对滑片与滑槽之间的摩擦问题可以建立LuGre摩擦模型进行分析,摩擦模型的建立关键在于模型中的6个参数的识别。
本文对滑片-滑槽的LuGre摩擦模型的参数识别问题进行研究,利用自适应权重粒子群优化算法对摩擦模型的4个静态参数进行识别,利用不同预滑移阶段的摩擦力值对摩擦模型的2个动态参数进行识别,获得能够描述滚动活塞压缩机滑片周期性变化摩擦的LuGre摩擦模型并验证其准确性,为分析滑片与滑槽之间的摩擦行为提供依据。
1 滑片与滑槽的摩擦模型
1.1 滑片与滑槽的工作特点
滚动活塞压缩机的滑片在滑槽中做周期性高速往复运动,运动距离较短,其结构和受力情况如图1所示。滑槽对滑片具有正压力FH,结合滑片与滑槽的相对运动导致了摩擦力Ff的产生,正压力FH源于工作过程中高压腔和低压腔的压力。

图1 滚动转子压缩机结构
1.2 建立LuGre模型
LuGre模型认为2个接触表面的摩擦力源于由相对运动导致的鬃毛挠曲变形[1,16]。本文以文献[17]分析的某定型压缩机的滑片与滑槽为研究对象,其结构尺寸为设计常量,结合滑片的结构和受力特点,该型号压缩机的滑片与滑槽的LuGre模型表示为:
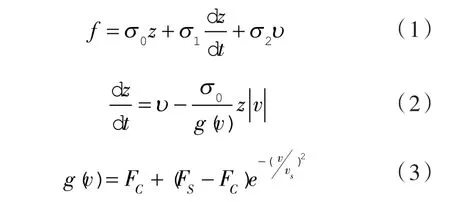
式中 σ0——鬃毛具有的刚度系数;
σ1——阻尼系数;
σ2——黏性摩擦系数;
v——滑片与滑槽之间的相对速度;
g(v)——Stribeck的负斜率效应;
FC——库仑摩擦力;
FS——最大静摩擦力;
vs——Stribeck速度。
LuGre摩擦模型中有6个需要识别的参数,其中动态参数包括σ0和σ1,静态参数包括σ2,FS,FC和vs。在非变温的工况条件下,滑片刚度系数由材料性质和材料结构等决定,与其受到的正压力FH无关;滑片的阻尼系数与其受到的正压力FH相关很小,其值与材料性质和环境温度密切相关。因此2个动态参数取固定值,不考虑正压力FH的影响。
对静态参数进行分析。Stribeck速度vs为固定值,不受FH影响。依据压缩机滑片的受力特点,考虑正压力FH的直接影响,滑片受到的最大静摩擦力FS和滑动摩擦力FC可以表示为:

式中 μC,μS——库仑摩擦因数、静摩擦因数。
在匀速vs状态下的稳定摩擦力FSS为:

滑片的黏性摩擦系数σ2与正压力FH存在近似线性的关系。通过试验获得FH与σ2的拟合关系曲线,将σ2表示为FH的函数,从而可以表示任意FH下对应的σ2,所以σ2可以表示为:
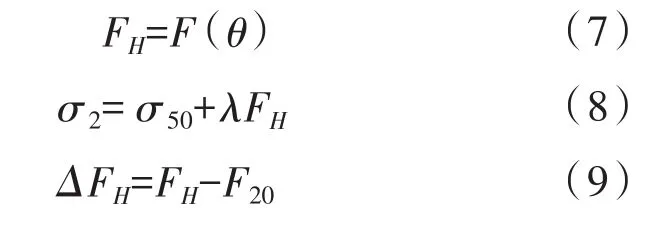
式中 F(θ)——正压力偏离转轴转角θ的函数;
σ50——FH=50 N时候的黏性摩擦系数;
λ——σ2与FH关系曲线的拟合系数。
可见压缩机在一个周期内,滑片与滑槽的LuGre摩擦模型由式(1)~(9)构成。LuGre摩擦模型中的σ0,σ1,σ2,μc,μs和 vs6 个参数通常需要通过试验来识别得到。
2 静态参数辨识
2.1 自适应权重PSO算法
粒子群优化算法简称为PSO算法,PSO算法中的粒子需要不断更新自身的空间位置x和速度v。
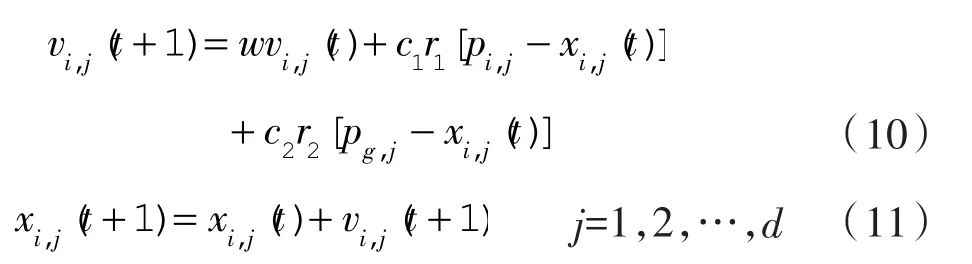
式中 w——惯性权重因子;
c1,c2——正的学习因子;
r1,r2——随机数,在0到1之间均布。
PSO算法可以采用非线性的动态惯性权重系数:
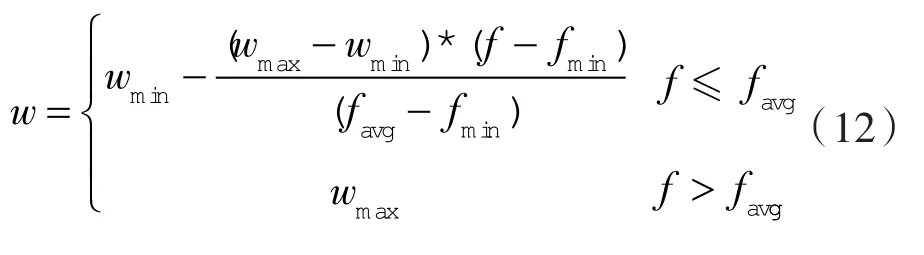
式中 wmax,wmin——w的最小、最大值;
f——粒子在当前状态下的目标函数值;
favg——当前状态下全部微粒的平均目标值;
fmin——当前状态下全部微粒的最小目标值。
自适应权重法就是:随着微粒的目标函数值的改变,惯性权重w可以自动改变。PSO算法求解流程如图2所示。

图2 PSO算法求解流程
2.2 静态参数识别及结果
为了实现通过自适应权重PSO算法来识别摩擦模型中的4个静态参数,需要将非线性的静态参数的识别问题转变成适应度函数的最小值问题。文献[17]建立了压缩机滑片与滑槽的摩擦力测试系统,并测量了正压力FH=50 N和FH=40 N时候的摩擦力与速度关系曲线和摩擦力与预滑移位移关系曲线。这些试验测量结果可以用来实现4个静态参数的识别和验证。正压力FH=50 N时不同速度下的摩擦力测量值见表1。
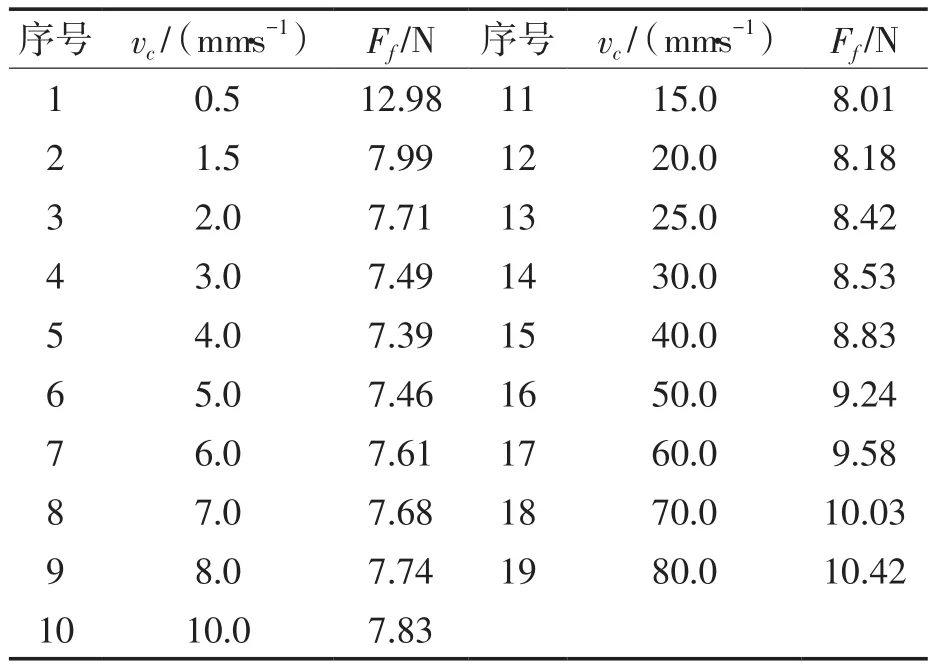
表1 不同速度下的摩擦力测量值(FH=50 N)
本文以正压力FH=50 N时候作为摩擦模型的基准点,此时FH=0 N,实测的摩擦力与待识别的摩擦力之间的拟合度较高,即偏差平方和最小。
因此,适应度函数Q可以表示为滑片与滑槽的实测摩擦力与待识别模型中计算输出摩擦力的偏差平方和。

式中 n——样本个数;
fi——实测摩擦力;
设置粒子的数量为40,学习因子是2,最大的惯性权重是0.9,最小惯性权重是0.6,迭代数是5 000。通过MATLAB软件调用SAPSO函数进行摩擦模型静态参数的识别。识别的结果为:σ2=0.35 2,μc=0.15,μs=0.25,vs=2.6。
3 动态参数辨识
3.1 平均刚度参数的σ2识别
LuGre模型将2个表面的接触摩擦等效成有弹性的刚毛的接触,因此在滑片的速度和加速度在预滑移阶段均很小,可以认为:

式(14)代入式(13)可得:

为了获得滑片与滑槽之间的摩擦力与预滑移曲线关系,将滑槽中的滑片组进行低速滑动,位移值为0.1 mm时候自动反向移动,测量这个过程中的摩擦力变化情况,得到曲线如图3所示。通过该曲线可以获得摩擦力差值和对应的位移差值,代入式(14)进行计算并取平均,得到平均刚度σ0=3.906 25×105。

图3 摩擦力位移曲线
3.2 阻尼系数σ1的识别
滑片产生预滑移的过程与二阶阻尼系统发生的受迫振动类似,因此有:
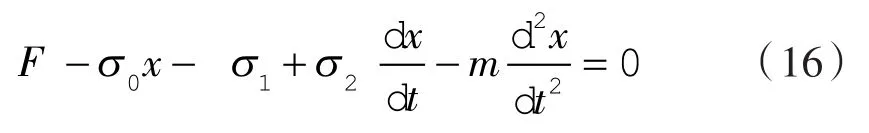
式中 F——滑片受到的载荷。
存在滑片受到的载荷F=0的情况,则式(16)变为:
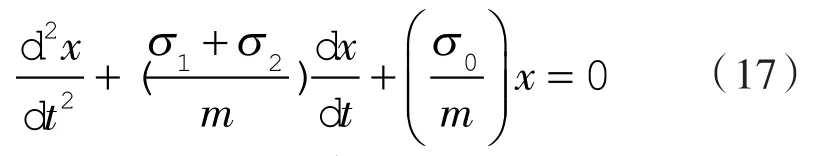
式(17)通过固有频率ωn和阻尼比ξ可表示为:
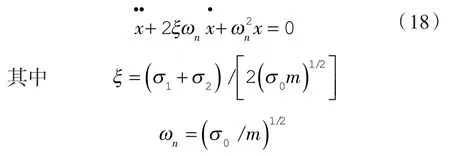
可以得到σ0,σ1和σ2三者的关系为:

将参数σ0=3.906 25×105,σ2=0.035 2,ξ=0.6代入式(19)可得σ1=589.8。
4 摩擦模型准确性的验证
通过静态参数和动态参数的识别,得到滑片与滑槽的LuGre摩擦模型,通过MATLAB软件对摩擦模型进行仿真分析,得到FH=40 N时的摩擦力与速度关系曲线。将仿真计算的曲线与文献[17-18]中试验测试得到的曲线进行比较如图4所示。模型仿真计算结果与试验测量结果基本一致。滑片与滑槽的LuGre摩擦模型得到了验证。
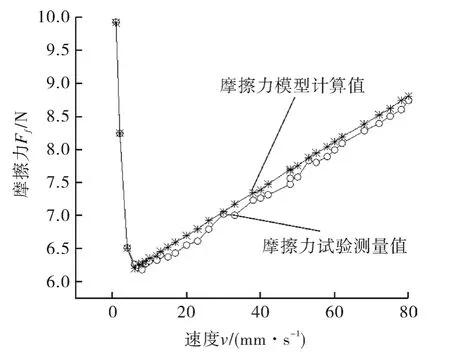
图4 摩擦力-速度的关系曲线(FH=40 N)
5 结论
(1)根据滚动活塞压缩机滑片与滑槽的工作特点和结构特征,建立了滑片与滑槽的LuGre摩擦模型,并提取出4个静态参数和2个动态参数。
(2)对滑片与滑槽LuGre摩擦模型的4个静态参数的特征进行分析,利用自适应权重PSO算法对静态参数进行识别。
(3)对滑片与滑槽LuGre摩擦模型的2个动态参数的特征进行分析,利用近似二阶阻尼系统发生的受迫振动的特点进行识别分析。
(4)应用MATLAB软件对摩擦模型进行仿真分析并与试验测试的结果进行对比分析,滑片与滑槽的LuGre摩擦模型得到了验证。
