梯图的邻点可区别均匀I-全染色

王继顺， 左 林， 李步军

(1. 连云港师范高等专科学校数学与信息工程学院， 江苏 连云港 222006；2. 淮海工学院 数理科学系， 江苏 连云港 222005)

1 基本概念与引理

图的染色理论被广泛应用于如网络优化和信息技术等领域中， 用来解决实际问题． 因此， 其理论及应用成为图论工作者研究的重要课题． 为满足应用的需要， 图的新染色方法被不断提出[1-4]，ZhangZhongfu等[3]提出图的邻点可区别I-全染色概念，王继顺等[4]提出了邻点可区别I-均匀全染色的概念，由于其都是NP完全问题，受到图论学者的普遍关注，杨随义等[5]研究了冠图的邻点可区别I-全染色，王继顺研究了蛛网图、渔网图[6]以及联图Pm∨Fn和Pm∨Wn[7]的邻点可区别I-全染色， 刘秀丽[8]研究了某些Mycielski图的邻点可区别I-全染色， 王笑妍等[9]研究了风车图、 齿轮图等图的均匀邻点可区别I-全染色， 给出了这些图的邻点可区别I-全色数或邻点可区别均匀I-全色数．

定义1[3]设G(V,E)是阶数至少为2的简单连通图, 令T(G)=V(G)∪E(G), 若存在一个正整数k和映射f∶T(G)→{1, 2, 3,…,k}, 使得

1) 对 ∀uv∈E(G),u≠v, 有f(u)≠f(v);

2) 对∀uv,uw∈E(G),v≠w,有f(uv)≠f(uw);

3) 对∀uv∈E(G),u≠v,有C(u)≠C(v);

则称f为G的一个邻点可区别I-全染色 (简记为k-I-AVDTC). 而称

定义2[4]设f是简单连通图G(V,E) (|V(G)|≥2)的一个k-I-AVDTC, 若满足对∀i,j∈{1,2,…,k},i≠j， 有

||Ti|-|Tj||≤1,

则称f为G的一个k-邻点可区别均匀I-全染色 (简记为k-I-AVDETC). 而称

为G的邻点可区别均匀I-全色数, 其中Ti=Vi∪Ei,Vi={v|v∈V(G),f(v)=i},Ei={e|e∈E(G),f(e)=i}.

由上述定义, 显然有

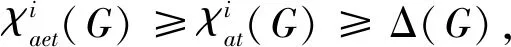
(1)

式中： Δ(G)表示G的最大度数.

引理1[4]对|V(G)|≥2的连通图G, 若有最大度点相邻, 则

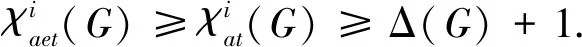
(2)

猜想[4]设简单连通图为G(V,E), 则

(3)

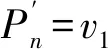
易见梯图Ln与笛卡儿积图P2×Pn是同构的图， 即Ln≅P2×Pn.

梯图是一种重要的网络图， 图论学者包世堂、 张薇、 王治文等研究了它的点可区别的全染色[10-13]， 本文将研究梯图Ln的邻点可区别均匀I-全染色问题, 通过分析该类图的结构特点, 运用所构造的有序颜色组循环对边和点染色， 并辅以色调整技术， 给出这类图的邻点可区别均匀I-全染色法， 并最终得到它们的邻点可区别均匀I-全染色数.

2 主要结果与证明

定理1设梯图Ln(n≥2), 则

(4)

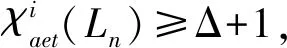
情形2.1当n≡0(mod 4)时, 对Ln进行循环染色， 构造从T(Ln)到{1, 2, 3, 4}的染色法f. 对顶点v1k(k=1,2,…,n)染色是用色1,2,3的有序染色组染过i=1, 2,3的顶点后， 循环向后染i直到n的顶点， 而对顶点v2k(k=1,2,…,n)的染色就是把对v1k(k=1,2,…,n)染色的染色组(1，2，3)轮换为有序染色组(2,3,1)， 然后循环向后染色. 对顶点的染色可归纳为

对Ln的边也作循环染色， 先对边v1kv1(k+1)(k=1,2,…,n-1)用一组有序染色组(1,2,3)染过k=1, 2,3的边后， 循环向后染i直到n-1的边， 而对边v2kv2(k+1)(k=1,2,…,n-1)的染色就是把对v1iv1(i+1)(i=1,2,…,n-1)染色的有序染色组(1，2，3)轮换为有序染色组(2,3,1)， 然后循环向后染色； 对所有的边v1kv2k(k=1,2,…,n)都染以色4. 对边染色可归纳为

k=1,2,…,n-1;

k=1,2,…,n-1;

f(v1kv2k)=4,k=1,2,…,n.

易见, 该染色法f满足定义1， 即是Ln(n≡0(mod 4))的一个4-I-AVDTC， 并且n=4时，f已是Ln的一个4-I-AVDETC， 但当n>4时， 它还不是均匀的， 为此对边或顶点的染色进行个别调整. 这里， 只要把顶点v2(n-1)的染色由原来的2重新定义为4即可， 即令f(v2(n-1))=4. 此时， 各顶点的染色集合为

C(v11)={1,4}，;

C(v21)={2,4};

k=2,3,…,n.

不同色所染元素数为

从而, 所给染色法f是Ln当n≡0(mod 4)时的一个4-I-AVDETC.

情形2.2当n≡1(mod 4)时, 对Ln进行循环染色， 构造从T(Ln)到{1,2,3,4}的染色法f. 按照n≡0(mod 4)的染色方法f来染n≡1(mod 4)时的Ln， 只需要调整染色， 当n=5时， 令f(v2(n-1)v2n)=3， 当n>5时令f(v1(n-1))=4即可. 但为了尽量少做调整， 下面改换一个染色方法f. 对Ln的顶点v1k(k=1,2,…,n)用有序染色组(1,2,3,4)染过i=1,2,3,4的顶点后， 循环向后染i直到n的顶点， 而对顶点v2k(k=1,2,…,n)的染色就是把对v1k(k=1,2,…,n)染色的有序染色组(1，2，3，4)轮换为有序染色组(2,3,4,1)， 然后循环向后染色. 对顶点染色可归纳为

对Ln的边也作循环染色， 先对边v1kv1(k+1)(k=1,2,…,n-1)染色， 用一组有序染色组(1,2,3,4)染过k=1, 2,3,4的边后， 循环向后染i直到n-1的边， 而对边v2kv2(k+1)(k=1,2,…,n-1)的染色就是把对v1iv1(i+1)(i=1,2,…,n-1)染色的有序染色组(1，2，3，4)轮换为有序染色组(2,3,4,1)， 然后循环向后染色； 将有序数组再作一次轮换得到(3,4,1,2)对所有的边v1kv2k对k=1,2,…,n的循环染色. 对边染色可归纳为

k=1,2,…,n-1；

k=1,2,…,n-1；

k=1,2,…,n.

上述所给出的染色法f不用做颜色调整即满足定义2， 这是因为各顶点的染色集合为

C(v11)={1,3}；

k=2,3,…,n;

C(v21)={2,3}；

k=2,3,…,n.

不同色的染色集合为

从而根据定义2, 该染色法f是Ln当n≡1(mod 4) 时的一个4-I-AVDETC.

情形2.3当n≡2(mod 4)时, 对Ln进行循环染色， 构造从T(Ln)到{1, 2, 3, 4}的染色法f. 按照n≡1(mod 4)的染色法f来染n≡2(mod 4)时的Ln， 只需要调整v1n的染色， 重新令f(v1n)=4即可. 此时， 各顶点的染色集合规律不变， 满足定义1， 而不同色所染元素数为

所以, 此染色法f是Ln当n≡2(mod 4)时的一个4-I-AVDETC.

情形2.4当n≡3(mod 4)时, 对Ln进行循环染色， 构造从T(Ln)到{1, 2, 3, 4}的染色法f. 同样按照n≡1(mod 4)的染色方法f来染n≡3(mod 4)时的Ln， 只需要调整v1(n-1)的染色， 重新令f(v1(n-1))=4即可.此时各顶点的染色集合规律不变， 满足定义1， 而不同色所染元素数为

所以, 此染色法f是Ln当n≡3(mod 4)时的一个4-I-AVDETC.

3 结 论

运用所构造的有序颜色组和其置换循环对边和点染色， 并辅以色调整技术， 给出了梯图Ln图的邻点可区别均匀I-全染色法， 并最终得到它们的邻点可区别均匀I-全染色数. 由于Ln≅P2×Pn， 后续工作将研究能否将该种方法对更一般的笛卡尔积图Pm×Pn进行邻点可区别均匀I-全染色， 从而有效确定该类图的邻点可区别均匀I-全色数.