基于约束规划的煤炭出港作业调度算法

李 伟，郑澜波

（武汉理工大学 物流工程学院，湖北 武汉 430063）

1 引言

我国是世界上最大的煤炭生产与消费国，庞大的消费量以及产销在地理上的差异，导致煤炭运输周期长、供应链结构复杂。港口作为煤炭多式联运中水陆模式的转运节点，其协调上、下游供需的作用直接影响着整条供应链的作业能力。据国家统计局数据，2014-2018年我国主要港口煤炭及制品吞吐量增长了10.26%，年均增长达3 811.75万t。在我国煤炭需求旺季，港口经常出现煤炭场存供不应求的现象，因此，对港口的堆场资源进行合理调度，最大程度地满足船舶需求是煤炭港口面临的重要问题[1]。目前，港口调度的研究集中在集装箱码头，而散货码头，更确切地说对于煤炭码头的研究较少[2]。输出型煤炭港口的运作模式可以分为拉动式（Pull-based）和推动式（Push-based），拉动式以客户需求为导向进行原煤运输和混配[2]，采用开放式的堆场，港口需要为每个到港煤堆分配堆存空间；而推动式则采用固定垛位模式，通过预测、安全库存等方式，事先在堆场堆存一定数量的原煤来满足客户的需求。

拉动式港口的研究可分为精确算法和启发式算法两个方向，由于港口调度问题的动态性和复杂性，精确算法想要达到较高的效率往往依赖于模型简化。文献[3]以巴西散货码头为研究对象，针对港口的主要作业环节建立了整体的混合整数规划（MIP，Mixed Integer Programming）模型，并提出一种结合列生成和分支定价算法的精确算法。考虑到煤堆矩形在堆场的时空布局与二维装箱问题的相似性，有学者将煤炭堆场调度问题转化成带特殊约束的二维装箱问题，并用约束规划（CP，Constraint Programming）范式对其进行建模。文献[4]分别建立了煤炭堆场空间调度问题的MIP模型和CP模型，并通过计算实验证明CP的求解效果更好。文献[5]结合两种规划范式的优势，将整体问题进行分解，分别用MIP和CP对港口调度主问题和堆场调度子问题进行建模，并提出一种基于benders分解的精确算法来提高模型求解效率。文献[3]和[5]的决策时间步长均为1h，相比而言，启发式算法能在更细的时间粒度下实现对堆场的精准调度。以典型的拉动式煤炭供应链HVCC（Hunter Valley Coal Chain）为例，文献[6]提出一种基于贪婪思想的遗传算法，该算法从全局和系统角度考虑了更全面的港口调度问题，并实现了煤炭出港作业在时空维度的连续调度。结合精确算法和启发式算法的优点，文献[7]以堆场为核心节点分别建立了煤炭供应的MIP和CP模型，通过滚动求解获得初始解，并设计了大规模邻域搜索算法对解进行改进，计算实验表明，CP的自定义搜索策略机制让其在求解中表现出更优异的性能。

我国大部分的煤炭港口采用推动式进行管理，其调度问题的文献研究主要基于规则和仿真方法，而基于数学模型和优化技术的研究较少。文献[8]将连续的堆场空间进行网格化处理，并提出了两种物料堆存方案，使用WITNESS软件对堆场离散时间进行仿真建模。文献[9]结合货物特性和堆场情况，提出三种堆存策略，并使用Plant-Simulation软件构建系统仿真模型对堆存方案进行实验和评价。文献[10]应用WITNESS软件对黄骅港的堆场进港作业系统进行仿真实验，并建立多目标MIP模型与之对比，发现MIP的求解效果更好。

在煤炭吞吐量逐年上涨的背景下，现有的基于规则和仿真的调度方法逐渐无法满足我国港口的日常运作要求。本文借鉴CP在拉动式港口应用的成功经验，以数学模型和优化技术为基础，为港口日常运作管理提供更合理、高效的调度算法。本文的研究对象为国内某大型出口配煤港口，该港的堆场分为四个部分，其中一期工程的建立时间最早，堆场结构也最复杂。因此，选取一期工程作为建模场景建立煤炭出港作业调度的CP模型，该模型充分考虑了固定垛位模式下的堆场作业特点，对于同类港口的调度问题具有普适性。为了解决问题动态性和组合性带来的求解困难，采用分而治之的思想将问题进行分解，并设计基于变邻域搜索的求解算法优化求解结果，从而实现求解效率和精度的平衡。

2 出港作业调度的约束规划模型

2.1 问题描述

一期工程共有6个条形堆场和8台取料机，堆场的空间布局如图1所示。每个条形堆场中坐落着多个垛位，垛位在堆场中占据一定的长度并存有一定数量的原煤。每个垛位的位置、煤种和存量信息已知，相邻垛位为防止污染会留有一段距离。取料机位于条形堆场两侧的轨道上，取料时，取料机沿着轨道行走到指定垛位旁，通过传送带将原煤转运至装船机，最后由装船机装载到靠泊船的对应舱位。

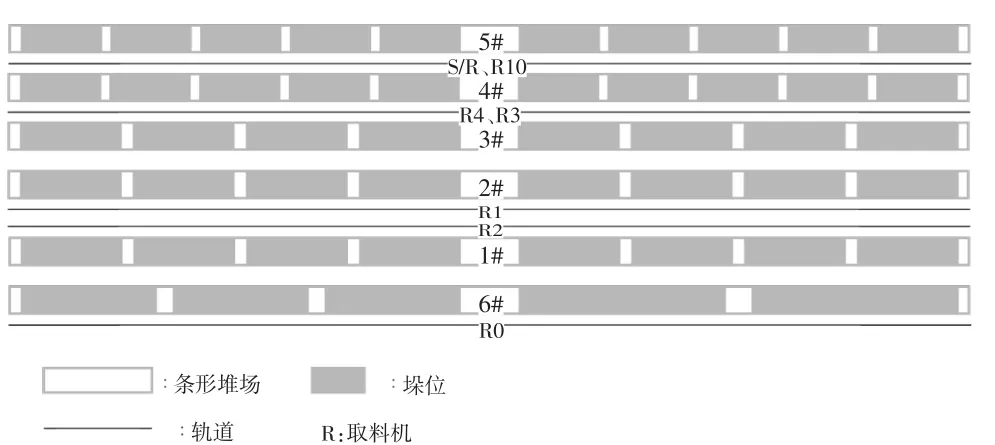
图1 堆场的空间布局示意图

客户到港前，会先向港口发出提名（Nomination）以告知船的预计到达时间和需求，一艘船一般需要一至三种合同煤。合同煤是指发热量、灰度等煤矿特性达到一定质量要求的煤种，由于推动式煤炭港口只存有数量有限的原煤，因此需要在装船过程中通过原煤混装形成客户需求的合同煤。每种合同煤一般由一至两种原煤按比例混合而成，称为配煤方案。此外，为了保持船体在水中的物理平衡，装船前还需要预先设定不同舱位的作业顺序。配煤方案选择和装船顺序可通过将问题转化为网络流模型求得[1]，本文模型不涉及配煤方案的选择且假定装船顺序已知。一艘船的装船任务实际上就是按顺序分轮、定量地装载原煤，每个轮次指定了所需原煤的种类和数量，由于单个垛位的存量有限，一种原煤时常需要在多个垛位取料。

图2是一个装船作业的过程示例，船舶v的装船作业分为3个轮次，轮次U1需要装载10 000t原煤C1，存有 C1的垛位为N105、N408和N604，实际作业在8：00到9：40从N105取料10 000t；轮次 U2需要20 000t原煤C2，由于单个垛位存量有限，因此从多个垛位取料完成该轮次作业；最后，轮次U3从唯一存有C3的N201取料完成作业。每次作业都是一个决策单元，称为装船单元，装船作业调度就是在船舶泊位和需求已知的情况下，为每个装船单元分配合理的取料时间、取料量和取料设备。由于堆场中存放的原煤种类较多且港口设备之间存在复杂的可达性约束，多条船舶同时在港作业可能会抢夺堆场的场存和设备资源，造成装船作业的延迟。装船作业的目的就是科学合理地调度堆场资源，让所有船能尽早完成作业离港。

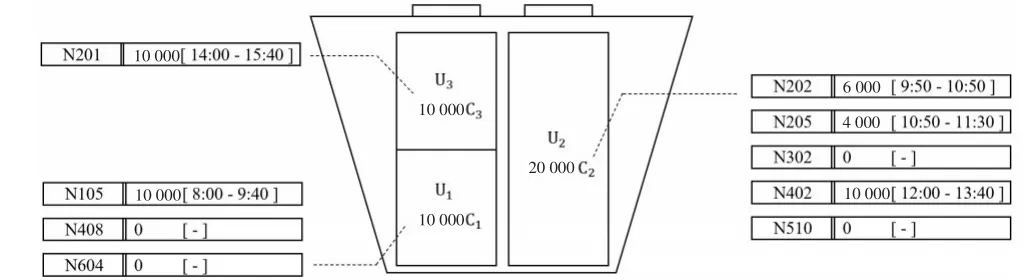
图2 船舶v取料装船作业示意图

2.2 模型假设

（1）所有到港船只的需求和停靠泊位已知，且所有决策不会超出预定的规划期。

（2）堆场中垛位的位置、煤种和存量信息确定且已知，场存充足。

（3）单次取料过程由取料机、传送带和装船机组成一条整体的作业线，其作业瓶颈为取料机，故以取料机能力为标准计算装船单元的取料时长。

（4）由于CP模型只能处理整数，故对数据进行取整处理，煤炭数量都取整为t，时间取整为min，距离取整为m，数据步长均为1。

2.3 符号说明

（1）集合

V为船舶集合，按预计到达时间排序；

U为轮次集合，按所属船舶的预计到达时间及装船顺序排序；

S为装船单元集合，按所属轮次排序。

（2）参数

etav为船舶v的预计到达时间，min；

Du为轮次u的取料量（时长），min；

vs为装船单元s所属的船舶；

us为装船单元s所属的轮次；

ns为装船单元s的取料垛位；

pn∈{0,...,1 300}为垛位n在条形堆场的位置，测算起点为距离泊位最远的堆场边界，m；

Rn为垛位n可用的取料机集合；

Qn为垛位n的场存量，t；

speedR=30为取料机的行走速度，m/s；

rateR=100为取料机的作业效率，t/min，所有设备的行走速度和取料效率一致。

（3）决策变量

rs∈Rns为装船单元s使用的取料机；

ts∈为装船单元s的取料开始时间，其中T为规划期的时间终点，min；

ds∈为装船单元s的取料时长，由于设备的取料效率一致，为方便建模，用取料时长代表取料量，min。

（4）辅助变量

依托乡土体育资源开展的阳光体育活动，改变了以往学生疲于应付，被动活动的局面，变“要我运动”为“我要运动”，使学生在文明和谐的氛围中陶冶情操，锻炼身体，让学生转瞬即逝的青春留下照亮终生的火花，让学生的人生充满了阳光，使他们无论是处于顺境还是逆境，都能乐观而不消极。

departv为船舶v完成作业任务离港的时间，即该船最后一个装船单元完成作业的时间，min。

2.4 约束规划模型

装船时间约束：装船单元的取料开始时间不能早于所属船的预计到港时间。

装船顺序约束：同一艘船分属不同轮次的装船单元需要按顺序装船。

船舶作业不重叠约束：同一艘船装船单元的作业时间不能重叠。

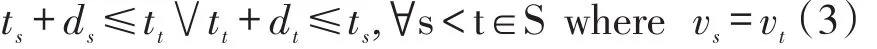
垛位作业不重叠约束：在同一个垛位取料的装船单元的作业时间不能重叠。

取料量约束：同属一个轮次的装船单元的取料量（时长）之和等于该轮次的总取料量（时长）。

垛位场存约束：任一垛位的取料量不能超过其场存量。

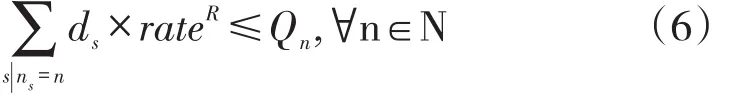
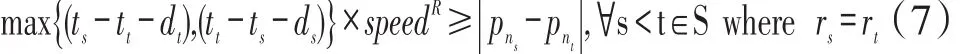
取料机防撞约束：条形堆场之间一般只有一条轨道，且按假设每条轨道只有一台取料机作业，而堆场1和堆场2之间有两条轨道，R1位于靠近堆场2的轨道上，R2靠近堆场1，当设备在各自靠近的堆场取料时，不会对彼此造成影响，否则将对另一台设备的行走产生限制。如图3所示，R2正在垛位N202取料，则位于其右侧的R1无法越过R2到左侧的N101和N201进行作业。

图3 取料机R2在N202取料时对R1行走产生限制

先考虑R2限制R1行走的情况，假设装船单元s使用设备R2在堆场2作业，则可能会对R1的作业产生影响，对任意一对先后由R1作业的装船单元t1、t2需要至少满足以下条件之一：t1、t2的设备移动发生在s作业之前或之后，即R1在时间上不会和R2产生冲突；t1、t2位于堆场的同一侧，即R1在空间上不会和R2产生冲突；在装船单元s作业开始之前或作业完成之后，R1有足够的时间从t1的垛位移动到t2的垛位，同理可得R1限制R2行走的情况。

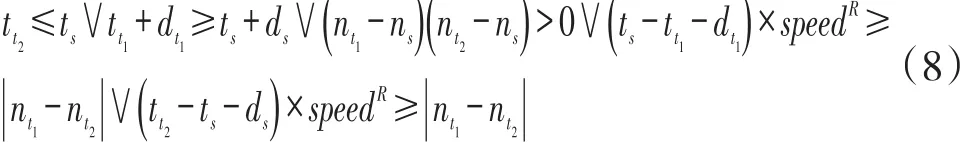
为了计算目标函数值，给出派生变量departv的计算公式，装船作业调度的目标是让所有船尽早完成作业离港，因此，目标函数为最小化船舶离港时间departv的累和。

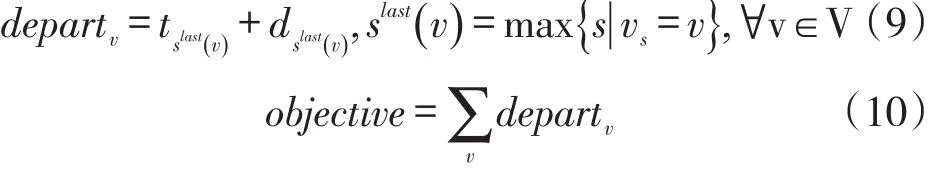
3 基于变邻域搜索的求解算法

在上述CP模型中，决策变量ts和ds共同构建了模型中大量的不重叠约束，导致一次性求解完整模型非常困难。因此，考虑将求解过程进行分解，先确定决策变量ds的取值，即装船单元的取料方案，再求解完整模型，并设计一种改进的变邻域搜索（VNS，Variable Neighborhood Search）算法优化取料方案。VNS是一种基于多邻域结构的元启发式算法，已被用于求解多个经典的组合或全局优化问题[12]，其主要思想是在搜索过程中系统地改变邻域结构，从而实现局部收敛和全局搜索的平衡。

3.1 算法主要组成部分

VNS只提供了求解问题的一般框架，本文根据问题结构，将概率和延迟思想引入到当前解更新的过程中，设计的VNS算法主要由五个部分组成：邻域结构的设计，这是基础和关键；初始解与邻域解的生成，实现解空间内的随机搜索；评价值计算与接受准则，用来更新当前解；延迟策略，实现解的局部收敛；终止条件。

3.1.1 邻域结构的设计。当有多个装船单元同时作业时，不同装船单元可能会抢夺堆场资源，造成作业延迟，邻域结构的设计思路是改变部分装船单元的取料量，通过调整不同轮次的取料方案消除作业冲突。应用VNS时，为了避免消耗过多计算时间，邻域结构的数量不宜过多，建议为2[13]。本文设计了N0和N1两种邻域结构，N1的结构由N0的搜索结果决定。

（1）邻域结构N0。假设装船单元的集合为S，装船单元i对应的取料量为di，则当前解可定义为，从 X1中 随 机 选 择 K1（如个变量进行扰动（改变变量的取值），固定其他变量取值，随机生成邻域解

（2）邻域结构N1。给定集合U′⊆U，假设当前解中 随 机 选 择 K2（如个变量进行扰动，要求被选变量所属的轮次u∈U′，固定其他变量的取值，随机生成邻域解

（3）N0和N1的关系。算法首先在邻域结构N0内搜索，如果当前解有所改进，说明改变部分装船单元的取料方案可以改进解的质量，将这部分装船单元所属的轮次U′记录下来，进入邻域结构N1，将其他轮次的取料方案固定，仅在更小的轮次U′范围内搜索邻域解。

3.1.2 初始解与邻域解的生成。初始解与邻域解的生成有两个要求，一是快速求解，二是保证解生成的随机性。考虑将CP模型中含有大量逻辑运算的约束（2）、（3）、（4）、（7）、（8）移除，并将最小化目标改为求可行解，形成简化的CP模型来求解取料方案。由于移除的约束不涉及决策变量ds，所以可以保证解的可行性。如前所述，邻域解的生成依赖于扰动变量的选择，假设当前解为X1，如果扰动变量选择不当，则邻域解X2可直接由约束（5）推出，此时X1=X2。为了保证邻域解的随机性，要求每次生成的邻域解满足，否则重新生成，直至满足条件。

简化的CP模型使用chuffed求解器的自由搜索（FS，Free Search）策略求解模型，FS的自适应搜索算法能进一步加快求解速度，并保证求解结果的随机性[11]。

3.1.3 评价值计算与接受准则。本文使用式（10）表示的目标函数值评价解的质量。用解表示的取料方案实例化CP模型中的取料时长变量ds，求出目标函数值作为解的评价值。在VNS的基本框架中，算法只接受改进的解来更新当前解。为了提高算法的全局搜索能力，本文借鉴模拟退火（SA，Simulated Annealing）的Metropolis准则，以一定概率接受较差的解。给定比例系数α，假设评价函数为 f()x，当前解为i，则接受邻域解 j的概率为：

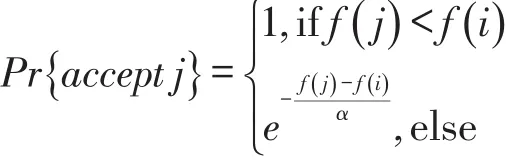
3.1.4 延迟策略。由于邻域解的产生具有随机性，因此每次当前解更新后，选择相同的变量继续扰动，寻找局部范围内的更优解。循环迭代，直至解在最近m次局部搜索没有得到改进，说明已经达到局部收敛，跳出循环进入下一步。

3.1.5 终止条件。使用两种条件判断算法是否终止运行：一是达到最大的迭代次数I，二是解足够接近全局最优。引入文献[2]中的理想离开时间作为问题的理论下界，理想离开时间（EPDT，Earliest Possible Departure Time）是指船v在港口资源无限的情况下最早完成作业离港的时间，即船的预计到达时间加上其装船单元的取料时长：EPDTv=etav+

3.2 算法框架

给定VNS的最大迭代次数I，VNS算法步骤如下：

Step 1 将场存数据Q和需求数据D载入到主程序。

Step 2 设置在邻域结构N0和N1内执行邻域搜索的迭代次数为n0和n1。设置k=0，i=0，n=0，其中k、i和n分别表示第k邻域结构、第i次迭代和第n次邻域内迭代。

step 3 生成初始解X0，设置当前解X=X0，最优解Xb=X0。

step 4 设置当前邻域结构为Nk，X执行迭代次数为nk的邻域搜索，在每次迭代中，使用接受准则判断是否接受邻域解，若接受，根据延迟策略对X执行局部搜索，转step5；否则，转step7。

step 5 如果X优于Xb，则更新Xb，转step6；否则，转step7。

step 6 设置n=-1、k=k+1，如果k＞1，则设置k=0。

step 7 更新参数i、n，判断是否达到终止条件，若是，则输出Xb，结束程序；否则，转step4。

4 数值实验

为了验证模型和算法的性能，本文根据港口历史数据生成了10组测试用例，每组用例的船舶数量为2～7，每艘船舶需求量为10 000～35 000t，轮次数量为6～25。图4是一个4艘船舶、11个轮次的测试用例求解的甘特图，每个矩形代表一个装船单元，矩形长度表示取料时长，标注分别表示取料垛位和设备。

本次实验在64位Windows10操作系统，intel®双核2.30GHz处理器，6G运行内存的电脑上完成。VNS算法使用Python3.6语言编写，VNS的参数设置为：最大迭代次数I=55，邻域N0内迭代次数n0=5，邻域N1内迭代次数n1=3，局部搜索参数m=3。CP模型使用专用的约束规划语言Minizinc2.3.2建模[11]，使用chuffed求解器求解。为了提高模型的求解效率，模型变量采用分组求解的策略，先从最重要的变量取料开始时间ts开始分支求解，之后依次确定取料时长ds以及取料设备rs。其中取料开始时间优先尝试可行域内的最小值进行搜索，取料设备选择可行域最小的变量先求解。由表1可以看出，制定求解策略后的模型求解效率得到大幅提升，CP的定制求解策略机制有利于充分发挥建模者的先验知识，帮助求解器更快找到好的解[7]。

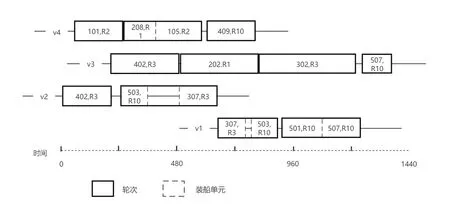
图4 测试用例的甘特图示例

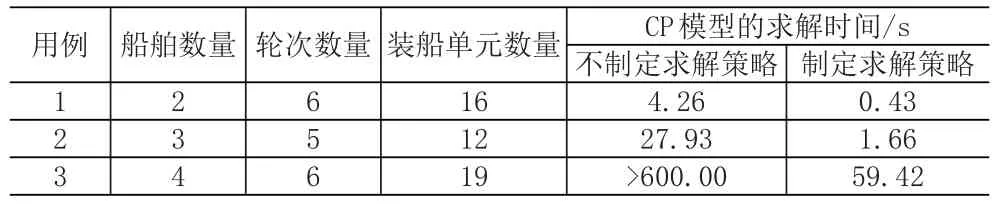
表1 制定求解策略对CP模型的影响

为了验证求解算法的有效性，将纯CP模型的求解结果和加入VNS的求解算法的求解结果进行对比，并使用前文所述的理论下界评价解的质量，求解时间设定为600s。从表2可看出，CP在数据规模较小的用例中求解效果好，用例1、2、3、4均能求得最优解，且仅有用例4的耗时比VNS长。在其他数据规模较大用例中，CP无法在限定的时间内求出结果，VNS则可以求得满意解，其在用例5、6的求解结果与理论下界的差距不到1%，其他用例的差距不到10%。

综合实验结果可知，对于小规模算例，纯CP的求解效果更好，但当数据规模较大时，CP已无法在有效时间内求解，而VNS则能得到较优的满意解。以上分析表明，基于VNS的求解算法是一种求解装船作业调度的有效算法。

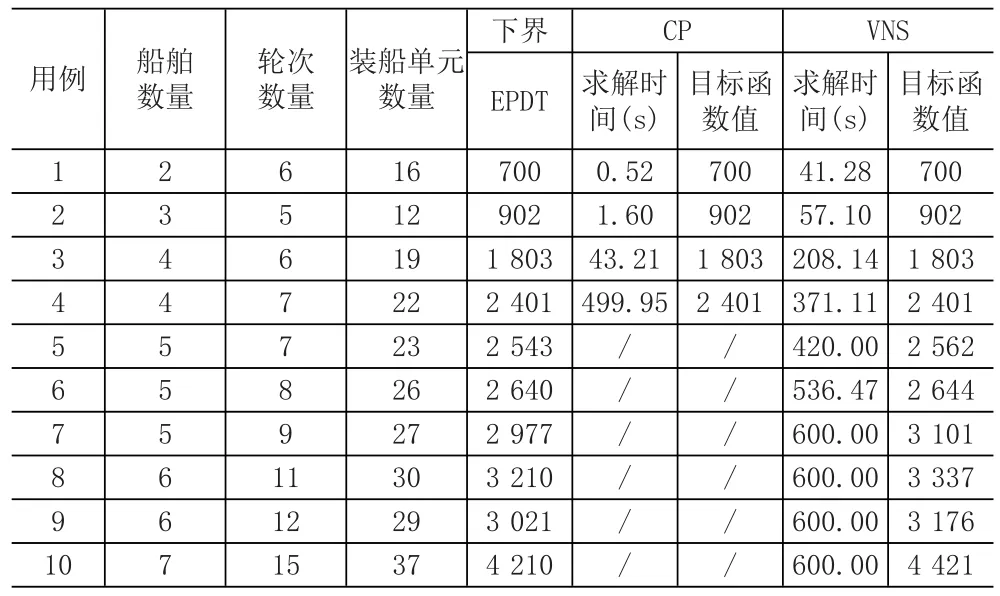
表2 CP与VNS的对比结果

5 结语

本文针对固定垛位模式下的煤炭出港作业调度问题，设计了结合CP和VNS的求解算法，算法求解分为两步，先确定装船的取料方案，再求解完整模型。将VNS引入到取料方案的优化中，其中当前解的更新采用Metropolis准则以一定概率接受劣解，并设计了一种延迟策略在每次解更新后加速算法的局部收敛。该方法综合考虑了出港作业调度问题的组合性和动态性，为提高煤炭港口的运作管理效率和水平提供了一种新的思路。